6.1: Background to D’Alembert’s Solution
- Page ID
- 8342
I have argued before that it is usually not useful to study the general solution of a partial differential equation. As any such sweeping statement it needs to be qualified, since there are some exceptions. One of these is the one-dimensional wave equation
\[\dfrac{\partial^2}{\partial x^2} u(x,t) - \frac{1}{c^2} \dfrac{\partial^2}{\partial t^2} u(x,t) = 0, \nonumber \] which has a general solution, due to the French mathematician d’Alembert.
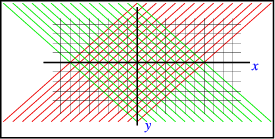
The reason for this solution becomes obvious when we consider the physics of the problem: The wave equation describes waves that propagate with the speed \(c\) (the speed of sound, or light, or whatever). Thus any perturbation to the one dimensional medium will propagate either right- or leftwards with such a speed. This means that we would expect the solutions to propagate along the characteristics \(x\pm ct=\text{constant}\), as seen in Figure \(\PageIndex{1}\).