Skip to main content
\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)
Mathematics LibreTexts

10.7: Our Initial Problem and Bessel Functions

  1. Last updated
  2. Save as PDF
  • Page ID
    8327

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    We started the discussion from the problem of the temperature on a circular disk, solved in polar coordinates, Since the initial conditions do not depend on \(\phi\), we expect the solution to be radially symmetric as well, \(u(\rho,t)\), which satisfies the equation

    \[\begin{aligned} \frac{\partial u}{\partial t} &= k\left[ \frac{\partial^2 u}{\partial \rho^2} + \frac{1}{\rho} \frac{\partial u}{\partial \rho} \right],\nonumber\\ u(c,t) &=0,\nonumber\\ u(\rho,0) &= f(\rho).\end{aligned}\]

    With \(u(\rho,t)=R(\rho)T(t)\) we found the equations

    \[\begin{aligned} \rho^2 R''+\rho R' + \lambda \rho^2 R &= 0\;\;\;\;R(c)=0\nonumber\\ T'+\lambda k T = 0.\end{aligned}\]

    The equation for \(R\) is clearly self-adjoint, it can be written as

    \[[\rho R']' + \lambda \rho R = 0\]

    So how does the equation for \(R\) relate to Bessel’s equation? Let us make the change of variables \(x= \sqrt{\lambda} \rho\). We find

    \[\frac{d}{d\rho} = \sqrt{\lambda} \frac{d}{dx},\]

    and we can remove a common factor \(\sqrt{\lambda}\) to obtain (\(X(x)=R(\rho)\))

    \[[x X']' + x X = 0,\]

    which is Bessel’s equation of order \(0\), i.e.,

    \[R(\rho) = J_0(\rho \sqrt{\lambda}).\]

    The boundary condition \(R(c)=0\) shows that \[c \sqrt{\lambda_n} = x_n,\]

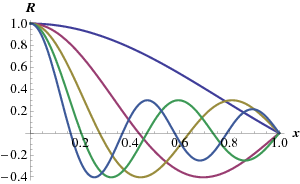
    where \(x_n\) are the points where \(J_0(x)=0\). We thus conclude \[R_n(\rho) = J_0(\rho \sqrt{\lambda_n}).\] the first five solutions \(R_n\) (for \(c=1\)) are shown in Fig. \(\PageIndex{1}\).

    BesselZero.png
    Figure \(\PageIndex{1}\): A graph of the first five functions \(R_n\)

    From Sturm-Liouville theory we conclude that

    \[\int_0^\infty \rho d\rho \,R_n(\rho)R_m(\rho)=0\;\;{\rm if\ }n \neq m.\]

    Together with the solution for the \(T\) equation,

    \[T_n(t)= \exp(-\lambda_n k t)\]

    we find a Fourier-Bessel series type solution

    \[u(\rho,t) = \sum_{n=1}^\infty A_n J_0(\rho\sqrt{\lambda_n})\exp(-\lambda_n k t),\]

    with \(\lambda_n= (x_n/c)^2\).

    In order to understand how to determine the coefficients \(A_n\) from the initial condition \(u(\rho,0)=f(\rho)\) we need to study Fourier-Bessel series in a little more detail.