8.3: Putting it all together
( \newcommand{\kernel}{\mathrm{null}\,}\)
In summary, we have u(ρ,ϕ)=A02+∞∑n=1ρn(Ancosnϕ+Bnsinnϕ).
The one remaining boundary condition can now be used to determine the coefficients An and Bn, U(c,ϕ)=A02+∞∑n=1cn(Ancosnϕ+Bnsinnϕ)={100if 0<ϕ<π0if π<ϕ<2π.
We find A0=1π∫π0100dϕ=100,cnAn=1π∫π0100cosnϕdϕ=100nπsin(nϕ)|π0=0,cnBn=1π∫π0100sinnϕdϕ=−100nπcos(nϕ)|π0={200/(nπ)if n is odd0if n is even.
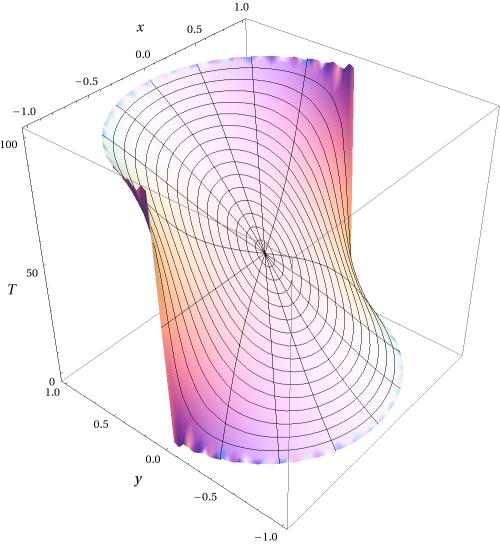
In summary u(ρ,ϕ)=50+200π∑n odd(ρc)nsinnϕn.
We clearly see the dependence of u on the pure number r/c, rather than ρ. A three dimensional plot of the temperature is given in Fig. 8.3.1.