10.2: Bessel’s Equation

Bessel’s equation of order $\nu$ is given by $$x^2 y'' + x y' + (x^2-\nu^2) y = 0. \nonumber$$ Clearly $x=0$ is a regular singular point, so we can solve by Frobenius’ method. The indicial equation is obtained from the lowest power after the substitution $y=x^\gamma$, and is

$$\gamma^2-\nu^2=0 \nonumber$$

So a generalized series solution gives two independent solutions if $\nu \neq \frac{1}{2} n$. Now let us solve the problem and explicitly substitute the power series,

$$y = x^\nu \sum_n a_n x^n. \nonumber$$

From Bessel’s equation we find

$$\sum_n(n+\nu)(n+\nu-1) a_\nu x^{m+\nu} +\sum_n(n+\nu)a_\nu x^{m+\nu} +\sum_n(x^2-\nu^2)a_\nu = 0 \nonumber$$

which leads to

$$[(m+\nu)^2-\nu^2] a_m= -a_{m-2} \nonumber$$ or $$a_m= -\frac{1}{m(m+2\nu)}a_{m-2}. \nonumber$$

If we take $\nu=n>0$, we have

$$a_m= -\frac{1}{m(m+2n)}a_{m-2}. \nonumber$$

This can be solved by iteration,

$$\begin{aligned} a_{2k} &= -\frac{1}{4}\frac{1}{k(k+n)}a_{2(k-1)}\nonumber\\ &= \left(\frac{1}{4}\right)^2\frac{1}{k(k-1)(k+n)(k+n-1)}a_{2(k-2)} \nonumber\\ &= \left(-\frac{1}{4}\right)^k\frac{n!}{k!(k+n)!}a_{0}.\end{aligned} \nonumber$$

If we choose¹ $a_0 = \frac{1}{n!2^n}$ we find the Bessel function of order $n$

$$J_n(x) = \sum_{k=0}^\infty \frac{(-1)^k}{k!(k+n)!} \left(\frac{x}{2}\right)^{2k+n}. \nonumber$$

There is another second independent solution (which should have a logarithm in it) with goes to infinity at $x=0$.

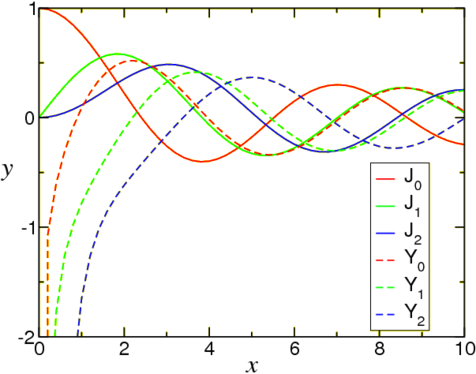
Figure $\PageIndex{1}$: A plot of the first three Bessel functions $J_n$ and $Y_n$.

The general solution of Bessel’s equation of order $n$ is a linear combination of $J$ and $Y$, $$y(x) = A J_n(x)+B Y_n(x). \nonumber$$

---

1. This can be done since Bessel’s equation is linear, i.e., if $g(x)$ is a solution $C g(x)$ is also a solution.↩