11.4: Modelling the eye–revisited

Let me return to my model of the eye. With the function as the solution to the angular equation, we find that the solutions to the radial equation are

The singular part is not acceptable, so once again we find that the solution takes the form

We now need to impose the boundary condition that the temperature is C in an opening angle of , and elsewhere. This leads to the equation

This leads to the integral, after once again changing to ,

These integrals can easily be evaluated, and a sketch for the temperature can be found in figure .

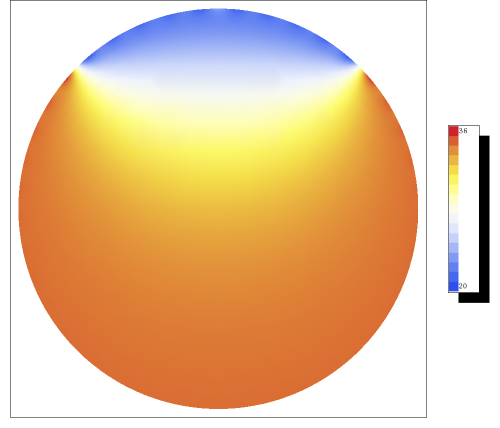
Figure : A cross-section of the temperature in the eye. We have summed over the first 40 Legendre polynomials.

Notice that we need to integrate over to obtain the coefficients . The integration over in spherical coordinates is , and so automatically implies that is the right variable to use, as also follows from the orthogonality of .