1.7: Angles
- Page ID
- 56588
Our next goal is to introduce angles and angle measures; after that, the statement “we can measure angles” will become rigorous; see (iii) on Section 1.1.
An ordered pair of half-lines that start at the same point is called an angle. The angle \(AOB\) (also denoted by \(\angle AOB\)) is the pair of half-lines \([OA)\) and \([OB)\). In this case the point \(O\) is called the vertex of the angle.
Intuitively, the angle measure tells how much one has to rotate the first half-line counterclockwise, so it gets the position of the second half-line of the angle. The full turn is assumed to be \(2 \cdot \pi\); it corresponds to the angle measure in radians. (For a while you may think that \(\pi\) is a positive real number that measures the size of a half turn in certain units. Its concrete value \(\pi \approx 3.14\) will not be important for a long time.
The angle measure of \(\angle AOB\) is denoted by \(\measuredangle AOB\); it is a real number in the interval \((-\pi, \pi]\).
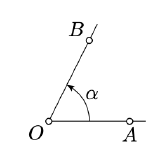
The notations \(\angle AOB\) and \(\measuredangle AOB\) look similar; they also have close but different meanings which better not be confused. For example, the equality \(\angle AOB = \angle A'O'B'\) means that \([OA) = [O'A')\) and \([OB) = [O'B')\); in particular, \(O = O'\). On the other hand the equality \(\measuredangle AOB = \measuredangle A'O'B'\) means only equality of two real numbers; in this case \(O\) may be distinct from \(O'\).
Here is the first property of angle measure which will become a part of the axiom.
Given a half-line \([OA)\) and \(\alpha \in (-\pi, \pi]\) there is a unique half-line \([OB)\) such that \(\measuredangle AOB = \alpha\).


