15.7: Duality
( \newcommand{\kernel}{\mathrm{null}\,}\)
Assume that a bijection P↔p between the set of lines and the set of points of a plane is given.
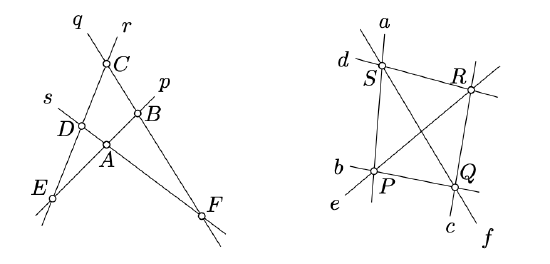
Dual configurations
That is, given a point P, we denote by p the corresponding line; and the other way around, given a line ℓ we denote by L the corresponding point.
The bijection between points and lines is called duality(The standard definition of duality is more general; we consider a special case which is also called polarity.) if
P∈ℓ ⇔ p∋L.
for any point P and line ℓ.
Consider the configuration of lines and points on the diagram.
Start with a generic quadrangle KLMN and extend it to a dual diagram; label the lines and points using the convention described above.
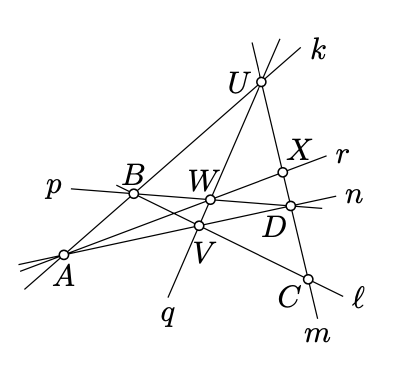
- Hint
-
Draw a=(KN), b=(KL), c=(LM), d=(MN), mark P=b∩d, and continue.
Show that the Euclidean plane does not admit a duality.
- Hint
-
Assume there is a duality. Choose two distinct parallel lines ℓ and m. Let L and M be their dual points. Set s=(ML), then its dual point S has to lie on both ℓ and m - a contradiction.
The real projective plane admits a duality.
- Proof
-
Consider a plane Π and a point O∉Π in the space; suppose that ˆΠ denotes the corresponding real projective plane.
Recall that Φ and Ψ denote the set of all lines and planes passing thru O. According to Observation 15.3.1, there are bijections P↔˙P between points of ˆΠ and Φ and ℓ↔˙ℓ between lines in ˆΠ and Ψ such that P∈ℓ if and only if ˙P⊂˙ℓ.
It remains to construct a bijection ˙ℓ↔˙L between Φ and Ψ such that
˙P⊂˙ℓ ⟺ ˙p⊃˙L
for any two lines ˙P and ˙L passing thru O.
Set ˙ℓ to be the plane thru O that is perpendicular to ˙L. Note that both conditions 15.7.1 are equivalent to ˙P⊥˙L; hence the result follows.
Consider the Euclidean plane with (x,y)-coordinates; suppose that O denotes the origin. Given a point P≠O with coordinates (a,b) consider the line p given by the equation a⋅x+b⋅y=1.
Show that the correspondence P to p extends to a duality of the real projective plane.
Which line corresponds to O?
Which point corresponds to the line a⋅x+b⋅y=0?
- Hint
-
Assume M=(a,b) and the line s is given by the equation p⋅x+q⋅y=1. Then M∈s is equivalent to p⋅a+q⋅b=1.
The latter is equivalent to m∋S where m is the line given by the equation a⋅x+b cdoty=1 and S=(p,q).
To extend this bijection to the whole projective plane, assume that (1) the ideal line corresponds to the origin and (2) the ideal point given by the pencil of the lines b⋅x−a⋅y=c for different values of c corresponds to the line given by the equation a⋅x+b⋅y=0.
Duality says that lines and points have the same rights in terms of incidence. It makes it possible to formulate an equivalent dual statement to any statement in projective geometry. For example, the dual statement for "the points X, Y, and Z lie on one line ℓ" would be the "lines x, y, and z intersect at one point L". Let us formulate the dual statement for Desargues’ theorem (Theorem 15.6.1).
Consider the collinear points X, Y, and Z. Assume that
Then the lines (AA′), (BB′), and (CC′) are concurrent.
In this theorem the points X, Y, and Z are dual to the lines (AA′), (BB′), and (CC′) in the original formulation, and the other way around.
Once Desargues’ theorem is proved, applying duality (Theorem 15.7.1) we get the dual Desargues’ theorem. Note that the dual Desargues’ theorem is the converse to the original Desargues’ theorem (Theorem 15.6.1).
Formulate the dual Pappus’ theorem (see Theorem 15.6.2).
- Hint
-
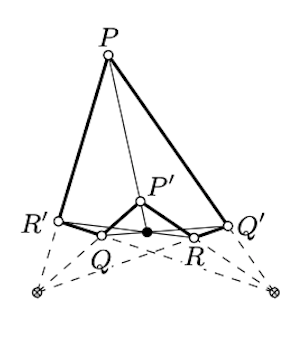
Assume one set of concurrent lines a,b,c, and another set of concurrent lines a′,b′,c′ are given. Set
P=b∩c′, Q=c∩a′, R=a∩b′,P′=b′∩c Q′=c′∩a, R′=a′∩b.
Then the lines (PP′), (QQ′), and (RR′) are concurrent. (It is a partial case of Brianchon's theorem.)
Solve the following construction problem
- using dual Desargues’ theorem;
- using Pappus’ theorem or its dual.
- Hint
-
Assume (AA′) and (BB′) are the given lines and C is the given point. Apply the dual Desargues' theorem (Theorem 15.7.2 to construct C′ so that (AA′),(BB′), and (CC′) are concurrent. Since (AA′)∥(BB′), we get that (AA′)∥(BB′)∥(CC′).
Now assume that P is the given point and (R′Q), (P′R) are the given parallel lines. Try to constuct point Q′ as in the dual Pappus' theorem (see the solution of Exercise 15.7.4).
Given two parallel lines, construct a third parallel line thru a given point with a ruler only.

