15.9: Axioms
( \newcommand{\kernel}{\mathrm{null}\,}\)
Note that the real projective plane described above satisfies the following set of axioms:
p-I. Any two distinct points lie on a unique line.
p-II. Any two distinct lines pass thru a unique point.
p-III. There exist at least four points of which no three are collinear.
Let us take these three axioms as a definition of the projective plane; so the real projective plane discussed above becomes its particular example.
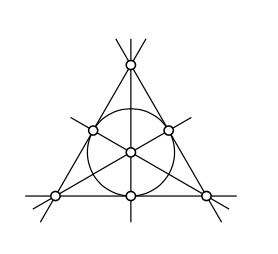
There is an example of a projective plane that contains exactly 3 points on each line. This is the so-called Fano plane which you can see on the diagram; it contains 7 points and 7 lines. This is an example of finite projective plane; that is, a projective plane with finitely many points.
Show that any line in projective plane contains at least three points.
- Hint
-
Let A,B,C, an D be the point provided by Axiom p-III. Given a line ℓ, we can assume that A∉ℓ, otherwise permute the labels of the points. Then by axiom p-I and p-II, the three lines (AB), (AC), and (AD) intersect ℓ at distinct points. In particular, ℓ contains at least three points.
Consider the following dual analog of Axiom p-III:
p-III': There exist at least four lines of which no three are concurrent.
Show that Axiom p-III' is equivalent to Axiom p-III. That is,
p-I, p-II, and p-III imply p-III',
and
p-I, p-II, and p-III' imply p-III.
- Hint
-
Let A,B,C, and D be the point provided by Axiom p-III. Show that the lines (AB),(BC),(CD), and (DA) satisfy Axiom p-III'. The proof of the converse is similar.
The exercise above shows that in the axiomatic system of projective plane, lines and points have the same rights. In fact, one can switch everywhere words "point" with "line", "pass thru" with "lies on", "collinear" with "concurrent" and we get an equivalent set of axioms — Axioms p-I and p-II convert into each other, and the same happens with the pair p-III and p-III'.
Assume that one of the lines in a finite projective plane contains exactly n+1 points.
- Show that each line contains exactly n+1 points.
- Show that the plane contains exactly n2+n+1 points.
- Show that there is no projective plane with exactly 10 points.
- Show that in any finite projective plane the number of points coincides with the number of lines.
- Hint
-
Let ℓ be a line with n+1 points on it.
By Axiom p-III, given any line m, there is a point P that does not lie on ℓ nor on m.
By axioms p-I and p-II, there is a bijection between the lines passing thru P and the points on ℓ. In particular, there are exactly n+1 lines passing thru P.
The same way there is bijection between the lines passing thru P and the points on m. Hence (a) follows. Fix a point X. By Axiom p-I, any point Y in the plane lies in a unique line passing thru X. From part (a), each such line contains X and yet n point. Hence (b) follows.
To solve (c), show that the quation n2+n+1=10 does not admit an integer solution and then apply part (b).
To solve (d), count the number of lines crossing a given line using the part (a) and apply (b).
The number n in the above exercise is called order of finite projective plane. For example the Fano plane has order 2. Let us finish by stating a famous open problem in finite geometry.
The order of any finite projective plane is a power of a prime number.

