20.7: Area of solid triangles
- Page ID
- 58354
Let \(a=BC\) and \(h_A\) to be the altitude from \(A\) in \(\triangle ABC\). Then
\(\text{area }(\blacktriangle ABC)=\tfrac12\cdot a\cdot h_A.\)
- Proof
-
Draw the line \(m\) thru \(A\) that is parallel to \((BC)\) and line \(n\) thru \(C\) parallel to \((AB)\). Note that the lines \(m\) and \(n\) are not parallel; denote by \(D\) their point of intersection. By construction, \(\square ABCD\) is a parallelogram.
Note that \(\blacksquare ABCD\) admits a subdivision into \(\blacktriangle ABC\) and \(\blacktriangle CDA\). Therefore, \[\text{area }(\blacksquare ABCD) = \text{area }(\blacktriangle ABC) + \text{area }(\blacktriangle CDA)\]
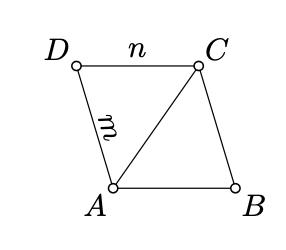
Since \(\square ABCD\) is a parallelogram, Lemma 7.5.1 implies that
\(AB=CD \quad \text{and} \quad BC=DA.\)
Therefore, by the SSS congruence condition, we have \(\triangle ABC\cong\triangle CDA\). In particular
\(\text{area }(\blacktriangle ABC) = \text{area }(\blacktriangle CDA).\)
From above and Proposition 20.6.1, we get that
\(\begin{aligned} \text{area }(\blacktriangle ABC) &=\tfrac12\cdot\text{area }(\blacksquare ABCD)= \\ &=\tfrac12\cdot h_A\cdot a\end{aligned}\)
Let \(h_A\), \(h_B\), and \(h_C\) denote the altitudes of \(\triangle ABC\) from vertices \(A\), \(B\) and \(C\) respectively. Note that from Theorem \(\PageIndex{1}\), it follows that
\(h_A\cdot BC=h_B\cdot CA=h_C\cdot AB.\)
Give a proof of this statement without using area.
- Hint
-
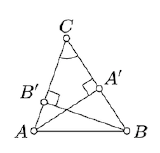
Without loss of generality, we may assume that the angles \(ABC\) and \(BCA\) are acute.
Let \(A'\) and \(B'\) denote the foot points of \(A\) and \(B\) on \((BC)\) and \((AC)\) respectively. Note that \(h_A = AA'\) and \(h_B = BB'\).
Note that \(\triangle AA'C \sim \triangle BB'C\); indeed the angle at \(C\) is shared and the angles at \(A'\) and \(B'\) are right. In particular \(\dfrac{AA'}{BB'} = \dfrac{AC}{BC}\) or, equivalently, \(h_A \cdot BC = h_B \cdot AC\).
Assume \(M\) lies inside the parallelogram \(ABCD\); that is, \(M\) belongs to the solid parallelogram \(\blacksquare ABCD\), but does not lie on its sides. Show that
\(\text{area }(\blacktriangle ABM)+\text{area }(\blacktriangle CDM) =\tfrac12\cdot \text{area }(\blacksquare ABCD).\)
- Hint
-
Draw the line \(\ell\) thru \(M\) parallel to \([AB]\) and \([CD]\); it subdivides \(\blacksquare ABCD\) into two solid parallelograms which will be denoted by \(\blacksquare ABEF\) and \(\blacksquare CDFE\). In particular,
\(\text{area } (\blacksquare ABCD) = \text{area } (\blacksquare ABEF) + \text{area } (\blacksquare CDFE)\).
By Proposition 20.6.1 and Theorem \(\PageIndex{1}\) we get that
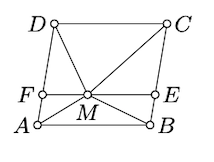
\(\begin{array} {l} {\text{area } (\blacktriangle ABM) = \dfrac{1}{2} \cdot \text{area } (\blacksquare ABEF),} \\ {\text{area } (\blacktriangle CDM) = \dfrac{1}{2} \cdot \text{area } (\blacksquare CDFE)} \end{array}\)
and hence the result.
Assume that diagonals of a nondegenerate quadrangle \(ABCD\) intersect at point \(M\). Show that
\(\text{area }(\blacktriangle ABM)\cdot\text{area }(\blacktriangle CDM) = \text{area }(\blacktriangle BCM)\cdot\text{area }(\blacktriangle DAM).\)
- Hint
-
Let \(h_A\) and \(h_C\) denote the distances from \(A\) and \(C\) to the line \((BD)\) respectively. According to Theorem \(\PageIndex{1}\),
\(\text{area }(\blacktriangle ABM) = \dfrac{1}{2} \cdot h_A \cdot BM\); \(\text{area }(\blacktriangle BCM) = \dfrac{1}{2} \cdot h_C \cdot BM\);
\(\text{area }(\blacktriangle CDM) = \dfrac{1}{2} \cdot h_C \cdot DM\); \(\text{area }(\blacktriangle ABM) = \dfrac{1}{2} \cdot h_A \cdot DM\).Therefore
\(\begin{array} {rcl} {\text{area } (\blacktriangle ABM) \cdot \text{area } (\blacktriangle CDM)} & = & {\dfrac{1}{4} \cdot h_A \cdot h_C \cdot DM \cdot BM =} \\ {} & = & {\text{area } (\blacktriangle BCM) \cdot \text{area } (\blacktriangle DAM)} \end{array}\)
Let \(r\) be the inradius of \(\triangle ABC\) and \(p\) be its semiperimeter; that is,\(p=\tfrac12\cdot(AB+BC+CA)\). Show that
\(\text{area }(\blacktriangle ABC)=p\cdot r.\)
- Hint
-
Let \(I\) be the incenter of \(\triangle ABC\). Note that \(\blacktriangle ABC\) can be subdivided into \(\blacktriangle IAB, \blacktriangle IBC\) and \(\blacktriangle ICA\).
It remains to apply Theorem \(\PageIndex{1}\) to each of these triangles and sum up the results.
Show that any polygonal set admits a subdivision into a finite collection of solid triangles and a degenerate set. Conclude that for any polygonal set, its area is uniquely defined.
- Hint
-
Fix a polygonal set \(\mathcal{P}\). Without loss of generality we may assume that \(\mathcal{P}\) is a union of a finite collection of solid triangles. Cut \(\mathcal{P}\) along the extensions of the sides of all the triangles, it subdivides \(\mathcal{P}\) into convex polygons. Cutting each polygon by diagonals from one vertex produce a subdivision into solid triangles.

