APPENDIX - Proof of the Z Theorem

Last updated
Save as PDF

Page ID: 34159

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

In section 1.4 we stated but did not prove the following theorem:

Theorem $\PageIndex{1}$ (The "Z" Theorem)

If two lines are parallel then their alternate interior angles are equal. If the alternate interior angles of two lines are equal then the lines must be parallel.

Theorem $\PageIndex{1}$ consists of two statements, each one the converse of the other, We will prove the second statement first:

Theorem $\PageIndex{1}$ (second part).

If the alternate interior angles of two lines are equal then the lines must be parallel. In Figure $\PageIndex{1}$, if $\angle x = \angle x'$ then $\overleftrightarrow{AB}$ must be parallel to $\overleftrightarrow{CD}$.

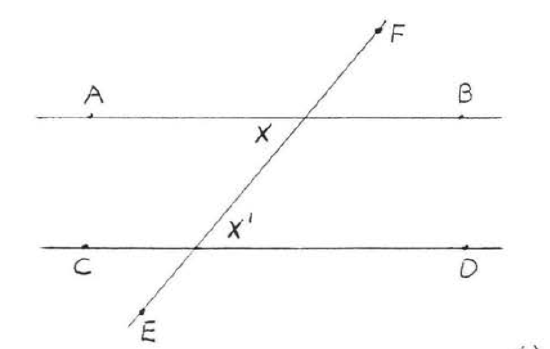
$Screen Shot 2021-01-19 at 8.50.29 PM.png$

Figure $\PageIndex{1}$. We will prove that if $\angle x = \angle x'$ then $\overleftrightarrow{AB}$ is parallel to $\overleftrightarrow{CD}$.

Proof

Suppose $\angle x = \angle x'$ and $\overleftrightarrow{AB}$ is not parallel to $\overleftrightarrow{CD}$. This means that $\overleftrightarrow{AB}$ and $\overleftrightarrow{CD}$ meet at some point $G$, as in Figure $\PageIndex{2}$, forming a triangle, $\triangle KLG$.

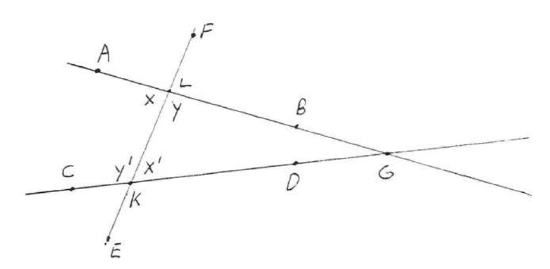
$Screen Shot 2021-01-19 at 8.57.36 PM.png$

Figure $\PageIndex{2}$. If $\overleftrightarrow{AB}$ is not parallel to $\overleftrightarrow{CD}$ then they must meet at some point $G$.

We know from the discussion preceding the ASA Theorem (THEOREM 2.3.1, section 2.3) that $\triangle KLG$ can be constructed from the two angles $\angle x'$ and $\angle y$ and the included side $KL$. Now $\angle x = \angle x'$ (by assumption) and $\angle y' = \angle y$ ($\angle y' = 180^{\circ} - \angle x' = 180^{\circ} - \angle x = \angle y$). Therefore by the same construction $\angle x$ and $\angle y'$ when extended should yield a triangle congruent to $\triangle KLG$. Call this new triangle $\triangle LKH$ (see Figure $\PageIndex{3}$). We now have that $\overleftrightarrow{AB}$ and $\overleftrightarrow{CD}$ are both straight lines through $G$ and $H$. This is impossible since one and only one distinct straight line can be drawn through two points. Therefore our assumption that $\overleftrightarrow{AB}$ is not parallel to $\overleftrightarrow{CD}$ is incorrect, that is, $\overleftrightarrow{AB}$ must be parallel to $\overleftrightarrow{CD}$. This completes the proof.

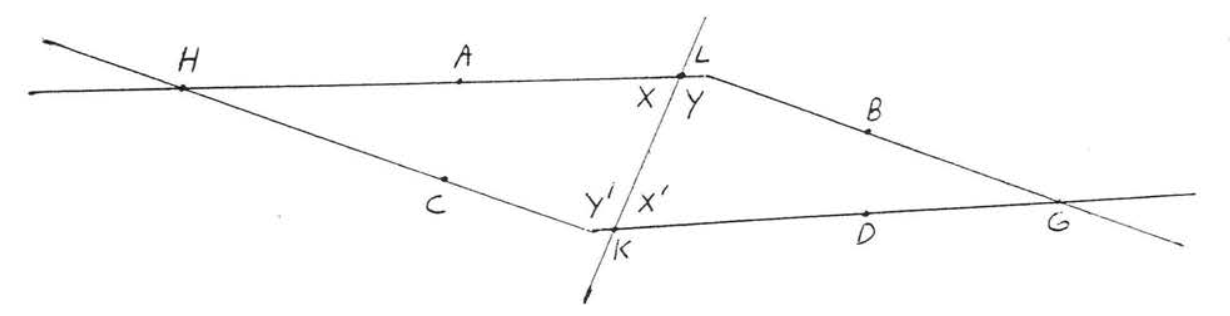
$Screen Shot 2021-01-19 at 9.04.21 PM.png$

Figure $\PageIndex{3}$. Since $\angle x = \angle x'$ and $\angle y' = \angle y$, $\angle x$ and $\angle y'$ when extended should also form a triangle, $\triangle LXH$.

Theorem $\PageIndex{1}$ (first part)

If two lines are parallel then their alternate interior angles are equal. In Figure $\PageIndex{4}$, if $\overleftrightarrow{AB}$ is parallel to $\overleftrightarrow{CD}$ then $\angle x = \angle x'$.

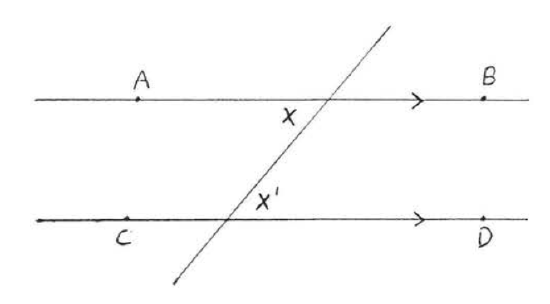
$Screen Shot 2021-01-19 at 9.10.19 PM.png$

Figure $\PageIndex{4}$. We will prove that if $\overleftrightarrow{AB}$ is parallel to $\overleftrightarrow{CD}$ then $\angle x = \angle x'$.

Proof

Suppose $\overleftrightarrow{AB}$ is parallel to $\overleftrightarrow{CD}$ and $\angle x \ne \angle x'$. One of the angles is larger; suppose it is $\angle x$ that is larger. Draw $\overleftrightarrow{EF}$ through $P$ so that $\angle w = \angle w'$ as in Figure $\PageIndex{5}$. $\overleftrightarrow{EF}$ is parallel to $\overleftrightarrow{CD}$ because we have just prove (THEOREM $\PageIndex{1}$, second part) that two lines are parallel if their alternate interior angles are equal. This contradicts the parallel postulate (section 1.4) which states that through a point not on a given line (here point $P$ and line $\overleftrightarrow{CD}$) one and only one line can be drawn parallel to the given line. Therefore $\angle x$ must be equal to $\angle x'$. This completes the proof of THEOREM $\PageIndex{1}$.

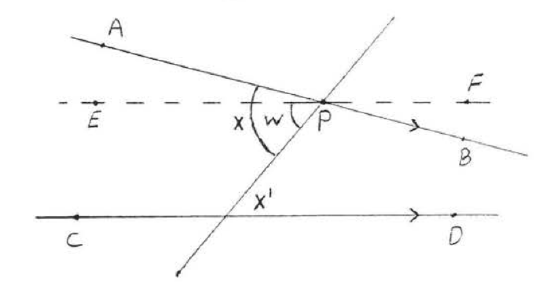
$Screen Shot 2021-01-19 at 9.15.34 PM.png$

Figure $\PageIndex{5}$. Draw $\overleftrightarrow{EF}$ so that $\angle w = \angle w'$.

Theorem \(\PageIndex{1}\) (The "Z" Theorem)

Theorem \(\PageIndex{1}\) (second part).

Theorem \(\PageIndex{1}\) (first part)