Preface

Introduction

The course begins with a review of several of the most elementary results of traditional Euclidean Geometry; in fact, those of the beginning of Book 1 of The Elements, the Euclidean original. Since this work is about 2300 years old, rights to the original are not a problem. For millennia, mathematicians have been convinced that the original Greeks and generations of mathematicians who followed them believed that "uniqueness of parallels" could be proved from more fundamental “axioms" about geometry (lit., "earth measure") that were so obvious that they could be safely assumed without proof. Standard content for a course called "Modern Geometry" involves proving that this is not the case and studying what happens under a different assumption.

Understanding what modern mathematicians mean by "proof" dates from this era and this work, The Elements. Many of us are convinced that, of all the contributions of the ancient Greeks to modern human thought, their ideas of deductive logic, concretized with mathematical proof, is the most important.

There have been many books written and good textbooks are available that cover the material of this course. Unfortunately, books that go deeply enough to develop the subject well assume a year of study, a semester is not sufficient especially for students with weak backgrounds. The standard approach is to develop more results of advanced Euclidean geometry first and to eventually back up and go into hyperbolic geometry. In order to get where we need to get, we will not formally develop some of the advanced Euclidean results that are logically needed because we would never get to the "modern" part of the course’s name. We will come back and develop, or at least introduce conceptually, some of these when we need them late in the course. Considerable compromise with mathematical formality will be sacrificed in order to meet this goal but not the idea of mathematical proof itself. In fact, the most important goal of the course is to solidify proving statements within the setting of Euclidean geometry. That the context may not be "Euclidean" can be very helpful in understanding the Euclidean setting itself. If you have never had any experience in proof-based Euclidean geometry, expect the course to be very difficult, maybe even too difficult for your success without exceptional effort on your part.

It will be assumed that you have a working knowledge of elementary logic; e.g., comfortable use of universal statements ("for every...” \(\forall\) ) versus existential statements ("there exists...” \(\exists\) ) where each ellipsis, "...”, is itself a statement. That backs us up even further; what is a "statement"? It is a sentence (in our case English but any language will do) that has "truth value"; it makes sense to call it "true" or "false" as opposed to, say, questions or commands. These ideas and much more elementary Euclidean geometry could be taken for granted up to the last few decades but, regrettably, that is no longer the case. The traditional high school course, usually "sophomore geometry", gave a very different background than many students - even strong students with math-based career aspirations - have experienced. I deeply believe that such students are shortchanged by this "progress" but reality is what it is. As a concrete example, one of the best and most popular books in Projective Geometry (including this campus - using this same course name and number!) within recent history - is A. Seidenberg’s Lectures in Projective Geometry, of the The University Series in Undergraduate Mathematics, 1962, of D. Van Nostrand Company, Inc. From the first paragraph of the Intro:

"The purpose of this book is to provide a text for an undergraduate course in Projective Geometry. The axiomatic approach to this subject is undoubtedly the proper one, but it seems desirable, if not necessary, to start from what the student knows, namely high school geometry, and proceed him from there to new things. Accordingly, the first chapter is devoted to introducing some of the main topics in as naive a form as possible.”

That "naïve a form as possible" of the first chapter should serve as a warning. I would defy more than two students in this class to read and understand it without some serious help; perhaps half of our semester would need to be devoted to get to the preparation UC Berkeley’s Abraham Seidenberg had in mind for the beginning of the course. If you have not had a fairly traditional proof-based Euclidean geometry course, finding an older high school geometry text or one from some of the community colleges (many of which have not lost their way) to study through can be a very helpful start (as in NOW!) for the course. Another opportunity is the rather amazing online free Khan Academy that can offer this "review" that may be far more than review but necessary for success in this course and for an appropriate understanding of proofbased geometry specifically and proof-based mathematics more generally:

https://www.khanacademy.org/math/geometry/

This is a first year, high-school level course on Geometry (which is based on Euclid’s elements). It revisits many of the basic geometrical concepts studied in earlier courses, but addresses them with more mathematical rigor. There is strong focus on proving theorems and results from basic postulates.

Proceeding (as in all of formal mathematics), a "statement" is a sentence that has an undefined "truth value" (hopefully, meaningful in the context) and new statements are constructed from existing ones in several ways. For a single statement, its negation means any reformulation of the statement such that if it was true, the new statement is false and inversely, if it was false, the new statement is true. Symbolically, if \(p\) is a statement, its negation is indicated by \(\sim p\) or \(\neg p\) or, less commonly, \(p^{\prime}\). Two or more statements can be compounded into new statements in several ways; the most obvious are and and or (formally, conjunction and disjunction that we will never use beyond this introduction along with their formal logic symbols, \(\wedge\) and \(\vee\) ). In the former case, the statement is true if and only if both (all, if more than two) statements are true and, in the latter, it is true if and only if at least one of them is true.

Back to universal and existential statements, their formal names will seldom be used and their formal symbols \((\forall\) and \(\exists\) ) never used. Also understood - but this time often used - will be the idea that to prove that a universal statement false requires only to exhibit one concrete counterexample (one example of the statement that is demonstrably false) or, as is sometimes more enlightening, a set of examples of the statement with some common property that shows all (that is important!) of them to be false. For a nonmathematical example, consider the statement, "All dogs are white". Obviously it is false and single counterexample, exhibiting a single brown (or any color(s) other than white) dog proves that it is false as does the set of all brown dogs (since that set is nonempty). One less obvious fact - but entirely standard throughout mathematics - unless otherwise qualified, general statements are assumed to be universal. As a geometry example, "An equilateral triangle is equiangular" is assumed to mean a statement about all equilateral triangles, not just some one of them, otherwise it would have to say something like, "Some equilateral triangle is equilateral", or equivalently, "Some equilateral triangles are equilateral", since the plural adjective "some" in logic means the same as "one or more"; i.e., "at least one".

Already being used in the introductory paragraph, is a "working knowledge" of conditional statements (also known as implications); i.e., "If..., then..." statements where each "..." is a statement. Slightly more formally, "If \(p\), then \(q\)," where \(p\) (the antecedent) and \(q\) (the consequent) are statements. In formal logic, this is written " \(p \Rightarrow q\) " (or " \(p \rightarrow q\) ") and will seldom be used except for here where it makes it more convenient to review relevant terms. First off, " \(p \Rightarrow q\) " is true except for one case, when \(p\) is true and \(q\) is false. For that reason, proving an implication is effected by assuming that \(p\) is true and proving that, with that assumption, \(q\) must also be true. On first acquaintance, this convention can seem to be counterintuitive but common sense logic does require that statements such as "If all dogs are white, then my dog is white" be considered to be true even if it is meaningless because, obviously, not all dogs are white but, in spite of the antecedent being clearly false, the statement must be taken to be true. If you are not convinced that that statement is meaningless, consider this slight modification, "If all dogs are white, then my dog is black." Again, the antecedent is false so the statement is taken to be true but, obviously, meaningless.

[Note: This is from the perspective of what is known as "propositional logic". This kind of ("quantified") statements are ordinarily considered from the perspective of what is known as "predicate logic."]

You might recall from logic that such an implication " \(p \Rightarrow q\) " is logically equivalent (i.e., one statement is true if and only if the other statement is true) to the compound statement " \((\sim p) \vee q\) " which is true if either \(\sim p\) is true (i.e., \(p\) is false) or \(q\) is true. That is, for the original implication to be true, either the antecedent \(p\) is false or the consequent \(q\) is true, hence the equivalence. If this does not seem familiar to you, it is easy to prove such statements using truth tables; i.e., directly confirm all possible truth values, in this case, four.

Back a few paragraphs, the word "inversely" was used although less careful but common useage might have said "conversely". The idea of the converse of an implication is critical in this course and throughout mathematics as are other permutations of the statements involved. Considering the general implication:

implication: \(p \Rightarrow q\) The permutations are:

converse: \(q \Rightarrow p\) That is, interchange the antecedent and consequent.

inverse: \(\sim p \Rightarrow \sim q\) That is, negate the antecedent and also the consequent.

contrapositive: \(\sim q \Rightarrow \sim p\) That is, both negate and interchange the antecedent and consequent.

Not a permutation of the original but a related statement that may or may not be true:

biconditional: \(p \Leftrightarrow q\) That is, both the implication and its converse: \(p \Rightarrow q\) and \(q \Rightarrow p\).

You should know (it’s easy to prove) that the original implication and its contrapositive are logically equivalent (one is true if and only if the other is true) as are its converse and its inverse (contrapositive implies that). Finally, the biconditional is true if and only if \(p\) and \(q\) are either both true or both false.

Of critical importance is the fact that the implication and its converse are not inherently logically equivalent (If my dog is white, then all dogs are white?) although it is often the case that implications in mathematics are biconditional; i.e., "if and only if" and abbreviated as "iff" For example, "A triangle is equilateral if and only if it is equiangular," or more succinctly, "A triangle is equilateral iff it is equiangular." At first glance, such a statement does not look like any kind of an implication but you need to equivalently and effortlessly think of it as, "If a triangle is equiangular then it is equilateral and conversely; i.e., if a triangle is equilateral then it is equiangular.”

The "think of it as" might seem backwards but is not. If this is not clear, you need to more carefully examine the position of the "if" and the "only if" in the statement. Leave off the "and only if" to more easily see the idea. Symbolically, that would say " \(p\) if \(q\) " that is almost obviously equivalent to "if \(q\), then \(p\) ". The "only if" is a little harder to understand at first but think about what " \(p\) only if \(q\) " must mean; it must mean that \(q\) follows from knowing \(p\) or, if \(p\) is true, then \(q\) must also be true. That is, if \(p\), then \(\mathrm{q}\). Hence the equivalence.

The first 28 propositions of the original Book 1 of Euclid’s Elements do not use "Euclid’s \(5^{\text {th }}\) ”, known as "The Parallel Postulate", and those propositions are where we will start the course. We will use them as a review of geometry and of proof itself in the familiar geometric setting. The language is archaic but I like both the history and the geometry. From a modern perspective, the ancient Greek’s introductory definitions are much too naïve and a few of the early propositions (SAS especially) need to be axioms or proved as consequences of unstated others but the presentation is surprisingly modern given the intervening millennia. The idea of trying so hard to avoid "the" Parallel Postulate (or any of the infinitely many statements that are logically equivalent) as long as possible is quite modern in its perspective. "As long as possible" is an exaggeration but the goal is evident and wasn’t answered for a couple millennia until the development of hyperbolic geometry by the Bolyais (mostly son Johann) and Nikolai Lobachevski in the 1830 s.

Many other theorems that "feel like Euclidean geometry" can also proved in "neutral" or "absolute" geometry (encompassing both Euclidean and hyperbolic geometry) that we will study in Chapter 2 such as "Hypotenuse-Leg", "construction of the incircle of a triangle", and "construction of the tangents from a point to a circle" along with many others that are provable in this context (no Parallel Postulate) before Chapter 3 where we specialize using the negation of the Parallel Postulate that (in conjunction with the other axioms of neutral geometry) is hyperbolic geometry.

Neither of these geometries is the "real world" in which we live; that is, on the surface of a sphere, a special case of elliptic geometry. Even there, many of the theorems hold with restrictions that figures not be "too big", whatever that might mean. This context can be helpful in understanding some results (so will occasionally be used herein) but are not to be considered as part of the negation of the Parallel Postulate because, given the other axioms, major differences arise. On a sphere, a "line" is a "great circle"; i.e., the plane of which contains the center of the sphere. Using a globe as a concrete model, all of the longitudinal lines are lines in the geometry but they all go through the North and South Poles so even the most fundamental, "two points determine a line", needs some kind of revision. As another example, consider three points in a row on the equator (a line in this geometry, other latitude circles are NOT lines)) A, B, and C. Now think of "sliding" \(C\) all the way around the globe to be lined up as \(C, A\), and B. Originally, B "felt like" it was between A and C. Now, it is A that has that feel with respect to \(C\) and B. The resolution? The concept of "betweenness" that is present and important in neutral geometry - does not exist in spherical geometry, at least not in the same unrestricted way. Still, thinking about spherical triangles and other geometric figures can be helpful in understanding validity and/or limitations of theorems in other geometry settings. When they fail to be true in spherical geometry, it helps us think more carefully about our proofs of the statements. Often the reasons explicit proofs fail are less than obvious. One enlightening example: On a sphere, any triangle - such as a triangle (ideally and perfectly) drawn on a poured concrete floor - has angle sum strictly greater than \(180^{\circ} !\)

From a modern perspective, the ancient Greek’s introductory definitions are much too naïve and a few of the early propositions (SAS especially) need to be axioms or proved as consequences of unstated others but, generally speaking, the presentation is surprisingly modern given the intervening millennia. This is the content of Chapter 1. After consideration of some common additional theorems in neutral geometry in Chapter 2, we will start discussing some properties and proving some theorems that are unique to hyperbolic geometry in Chapter 3. To most knowledgeable people on first introduction, these can seem to be quite counterintuitive, even wrong. Competence with formal deductive logic, i.e., proof, will make the results inevitable (from that starting point) but they still can have an air of make-believe. There is lots more to hyperbolic geometry than we will study but, again, we only have one term so this will only be a brief introduction with the primary goal being development of careful reading and proof in mathematics rather than content mastery of either hyperbolic geometry or advanced Euclidean geometry, both important topics worthy of study at this stage in your career.

The validity of the axioms of hyperbolic geometry is established by verifying "relative consistency" with Euclidean geometry; i.e., by establishing a model for this "new" geometry entirely within Euclidean geometry. That is, if anything is ever to be proved inconsistent in this new geometry, it would mean an inconsistency within the geometry that we all believe, Euclidean geometry. In reality, this is one long complicated Euclidean geometry theorem with lots of parts. To this end, a subset of the Euclidean plane is selected within which one redefines the constructs of "normal" geometry; i.e. giving new specifications of what to call points, lines, line segment measure, etc., and relationships among them. Within this setting, every axiom (postulate) of hyperbolic geometry must be proved as a Euclidean theorem; i.e., using any of the axioms and theorems of Euclidean geometry needed. That is, we are free to use conventional points, lines, etc., of the entire Euclidean plane, and all of the theorems among them, to prove each of the axioms of hyperbolic geometry as a theorem in the model. Many of the needed results in Euclidean geometry are not covered in introductory Euclidean geometry courses so we will need to introduce and study some of the properties of Euclidean geometry that are "well-known" but more advanced than high school geometry.

It should be noted that this consistency theorem is a trivial consequence of Complex Analysis (Linear Fractional Transformations and conformal mapping). However, most mathematics students don’t have that level of mathematical sophistication at this stage (and many never will!). Moreover, much is to be gained from the review of elementary Euclidean geometry as well as new material learned in the process (inversions in a circle especially). Even worse, sometimes the ideas in Complex Analysis are not proved but refer to the student’s knowledge Euclidean geometry. There is nothing wrong with this except that it can’t be used both ways; circular reasoning is a no-no in mathematics!

After arguing that semi-formal deductive logic was the most important gift of the ancient Greeks to modern human thought, and that geometry is an effective and the most common (somewhat) formal introduction to that process, it might come as a surprise that formal axiomatic development will not be done in this course. It’s even worse than that; the collection of axioms that we will use will never even be stated! The problem is that, in a genuinely formal development, even the underlying set theory and real analysis, would have to be axiomatically developed. Even taking naive set theory and properties of the real numbers for granted and focusing just on the geometry would still require a level of formality that would preclude getting much else done in the entire course. We will take the opposite extreme and only state the most critical of the axioms but how much formality will be expected is hard to quantify precisely. Hopefully, you will quickly develop a "feel" for it. In fact, you might have to "unlearn" some phony formalities; e.g., at this level and beyond, it is standard to ignore statements that are logically necessary but so obvious that their inclusion would be pedantic. Knowing what is "obvious" and what requires statements of verification can be tricky, of course; among other problems, it depends on the sophistication of both the writer and the target audience.

The terms axiom and postulate are taking to be interchangeable and mean statements that are accepted without proof. One of the "errors" of the Greeks was to assume that some statements are so obviously universally true as to always be true without proof and, therefore, a safe starting point. A more modern perspective is to leave the concept of "universal truth" out of the mix entirely. If we’re in a setting where the statements are true - a so-called "model" of the geometry - what else must be true because it has already been proved? If not, that’s fine too; we’re just in some other setting, perhaps equally useful, maybe even more so. The same statements may or may not be true but, if they are, they require new proofs.

Axiom 1 - (For the rest of the course!) - Two points determine a line.

If this does not seem familiar to you, you are probably in the wrong course! However, really knowing what it means is very different. What are "points"? What are "lines"? What does "determine" mean?

Perhaps surprisingly, (except within any model) point and line will be taken as undefined terms restricted by certain axioms (that are also never formally stated). More surprisingly, perhaps, is that in any axiomatic system, there must be undefined terms or the structure is inherently circular. At the set level, "set" and "element of a set" are undefined. Doesn’t a set mean a "collection of" or some such? Well, what does "collection of" mean? Etc., etc. That is, there is no place to stop so, over millennia, formal logicians have learned not to try. But, whatever they are, they behave in certain ways; i.e., according to statements called axioms. For set theory and the real or complex numbers, we will not even begin to try to say what they are axiomatically; we’ll just use them at will (along with most mathematicians nearly all of the time).

Before we begin, there are some properties of a set of axioms that need to be understood.

Most fundamental is that they need to be consistent; i.e., that they have no inherent contradictions. In other words, it is critical to be sure that they cannot lead to statements that can both be proved and disproved; i.e. proved to be both true and false within the system. Such a statement would destroy the entire structure.

Proving that no such inherent contradictions can arise is a challenge in itself. In fact, in a very real sense, it is an impossible task! Entirely within a system itself, it is impossible to prove that the axioms are consistent. The standard proof of consistency of a set of axioms is to produce a "model"; a concrete realization of the situation (and even "concrete" is in the eye of the beholder!) in which all of the axioms can be proved as theorems. For example, if we have enough faith in the ordinary Cartesian (x, y) plane, it provides an example of a model for Euclidean geometry and, with that assumption, the axioms of Euclidean geometry must be consistent. For abstract systems, the most we can logically hope for is relative consistency; if we accept one system to be consistent, use that to prove that another must also be.

A less critical but desirable property is that the axioms be independent. This means that it is not possible to prove any of them using only the others. Failing to have this property would not destroy the system but it is definitely preferred. The fewer and more fundamental the axioms are, the "cleaner" the structure. We might have encountered the Pythagorean Theorem in 6th or 7 th grade but it was not presented as the Pythagorean Axiom just because we couldn’t yet understand a proof. The idea was that it was taken to be true without our proof but not without somebody’s proof. Axioms are not just "pulled out of the air"; wise choice of them is a very sophisticated process and we won’t begin to try. We won’t even try to list them but some famous choices are easily available and will be referenced below.

A third property that a system might have is that the axioms be categorical. This is not always a desirable property since it implies that we are dealing in very specialized circumstances when, in mathematics, we often want to study properties that apply to many inherently different situations. For example, a "group" in mathematics is a specialized term that applies to lots of different structures that fit the group axioms but, if we add to them that the group has exactly seven elements, the set of axioms becomes categorical. In a very real sense, there is only one such group. That is, if the set of axioms is categorical, all "models" of the setting can be viewed as outwardly different forms of exactly the same thing. In the jargon, all models are "isomorphic." On the plus side, if a set of axioms are known to be categorical, a theorem proved in the context of one model must also be valid in all other models. As an example, if you are familiar with "analytic" proof versus "synthetic" proof in Euclidean geometry, knowing that the axioms are categorical assures us that either proof suffices. A theorem in any model is a theorem in the geometry. (See Chapt. 4.)

What is a model of the setting? Let’s keep it in the terms of plane geometry. A geometry is an abstract set of elements called "points", certain abstract subsets of which that are called "lines" and perhaps other special sets assuming they satisfy certain confining properties called axioms. A model for this geometry is, in some sense, almost the opposite. It is a very concrete set, the elements of which are called points, concrete subsets of these points called lines and circles, etc., and all of the axioms of the geometry (i.e., statements assumed without proof in the geometry) are proved as theorems in the model. At that point, all of the theorems of the geometry become theorems in the model as well; i.e., they have already been proved.

Here are two famous sets of axioms that are readily available:

• Hilbert’s Axioms for Euclidean Geometry:

• Birkhoff’s Axioms for Euclidean Geometry:

Note: Of these formal sets of axioms (that we will not be using formally), only Birkhoff’s (1959) includes what is known as a Ruler Postulate and a Protractor Postulate. However, Hilbert’s (1899 as revised in 1902) do imply results consistent with them [Google: Desargues/Pappus/field and/or see Blumenthal, \(A\) Modern View of Geometry, the V. H. Freeman & Co, 1961] and were revised to include them by Saunders MacLane in 1923. These were not used by the Greeks (although some of the same ideas were present but expressed in terms of comparisons of line segments (for length), polygons (for area), and angles (for angle measure). We will include them but use them somewhat informally as follows:

Ruler Postulate: There is a 1-1 correspondence between points on a given line and the real numbers that behave in "nice ways"; i.e., given a distance and a direction, there is a unique point determined and vice versa. That is, once the line is "coordinatized," each point corresponds to a unique real number, and this association of line segments is consistent with real number arithmetic. For line segments, this distance between its endpoints is called the measure of the line segment but the word "measure" is misleading; there is no measuring involved since all measurement is approximate and these are taken to be infinitely accurate.

Protractor Postulate: There is a 1-1 correspondence between angles starting from a given ray and the real numbers of a closed interval \([0,180]\) (or \([-90,90]\) or \([0, \pi]\) or \([-\pi / 2, \pi / 2]\) or any other such including ones that might be reasonable but are almost never used such as \([0,100]\) ) such that, given an angle size and a direction, there is a unique ray determined and vice versa. Once the semicircle is "coordinatized," each ray corresponds to a unique real number of the interval and, again, this association is consistent with the arithmetic of real numbers. This associated number is called the measure of the angle but, again, there is no measurement involved. Infinite precision is always assumed unless otherwise stated (almost never).

One last time, these ideas (especially their names) can be a little misleading; there is no actual measuring going on as that would be inherently approximate. These are theoretical abstractions only. Everything is assumed to be infinitely accurate which is never possible in measurement situations. Moreover, unless otherwise stated, infinite accuracy will be expected of you so calculators will be of little help except as a security blanket. Except for major exams, they will not be not prohibited but answers are expected to be precise; e.g., \(\pi\) is not \(3.14\) nor \(3.14159,2 / 7\) is not \(0.2857\), etc. Decimal answers are acceptable only if they are precise - decimal approximations will not receive full credit. Simplified ordinary fractions will suffice for the course and, in fact, are preferred whenever appropriate. Calculators, cell phones, and the like will be prohibited from the midterm and final because they have gotten too "smart"; i.e., they can record information and give you access to information that must be in your head to be able to think effectively.

How can we operate axiomatically without ever stating most of the axioms explicitly? Hopefully, you’ll get the idea as we progress. One of the important ideas about which we will be kind of "sloppy" is that of "betweenness" of points on a line but it has to "be there" whether we worry about it or not. Another is continuity considerations. Say, for example, a line segment is determined by a point inside a circle and another outside of it. It should be obvious - and we will take it for granted - that there is a point of intersection of that segment and the circle. Formal axioms are needed but they will be ignored.

The same idea applies to definitions. They are absolutely critical and yet many of them will not be given in the course, at least not explicitly. If there is any doubt about what is true "by definition" about a named object of some kind, ask, and make careful note of it in your own personal glossary. Stating that a property of some geometric structure is true by definition when it is not part of the definition, but has been proved instead, is a serious error so be careful. If there is any ambiguity, also include the name of the word being referenced; e.g., "by definition of rectangle" instead of just "by definition". [What is the definition of rectangle? A quadrilateral with all angles being right angles. Nothing more. Anything else must be proved.]

Abbreviations are another place where care must be exercised in the sense that their "full-blown" forms need to be clearly in mind. That is, an abbreviation should not be used unless both the writer and the reader can expand it equivalently and effortlessly. A good example in geometry is SAS. Unless you have weak English or math skills, you can read it immediately as "Side-Angle-Side." That is not what is meant by "expanding it"; that is just the abbreviation. SAS is a statement; that is, it is a full (in our case, English) sentence that has truth value. Moreover, it is a universal statement; in this case, a statement about all triangles that meet the SAS conditions. It is common in geometry - and in mathematics settings more generally - to assume universality (i.e., "for every...") of statements that "sound like it". In general, an abbreviation should not be used unless you can expand it unambiguously on demand and not as some kind of verbatim, rote response but exactly the same mathematical content with as few mathematical symbols and/or figures as practicable and consistent with the expansion that any other knowledgeable practitioner would give it. In addition to being a universal statement, SAS is an example of a conditional statement or implication; i.e., it is an "if..., then..." statement as discussed earlier with the SAS only being an abbreviation of its hypothesis, not its conclusion, much less the entire implication.

SAS: If two triangles have two pairs of sides congruent and the angles included by these pairs of sides congruent, then the triangles are congruent.

Is it true? At least it makes sense to ask so it is a statement! Explaining its meaning to someone who does not know what it means, would it be clearer if supported by a good figure with the conditions properly indicated. That, however, should be a triviality for the person using the statement and for the person who is reading or hearing it; otherwise, the abbreviation should not be used at all. Their pictures would have different shaped triangles (but neither should appear to be specialized; i.e., not right triangles, not isosceles, etc.) and would probably be labeled differently but they would be communicating exactly the same idea. One thing that probably would be the same would be the use of "congruence marks", standard "tick mark" indicators that line segments or angles are congruent and a special mark for right angles. USE THEM! Unfortunately, my most powerful graphics software, Cinderella, does not include them so there will be times when you will need to add them in yourself. That should be easy to do from the context. Another point, you may be used to seeing such statements presented artificially such as:

Given: \(\overline{\mathrm{AB}} \cong \overline{\mathrm{EF}}, \overline{\mathrm{AC}} \cong \overline{\mathrm{EG}}\), and \(\angle \mathrm{A} \cong \angle \mathrm{E}\) (or \(\angle \mathrm{BAC} \cong \angle \mathrm{FEG}\) )

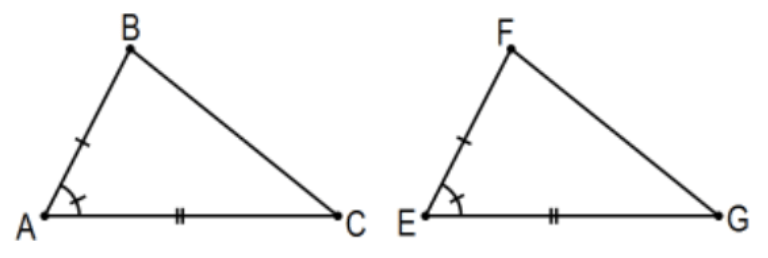
Conclusion: \(\triangle \mathrm{BAC} \cong \triangle \mathrm{FEG}\)

Note: Another (and worse!) limitation of my software is that it is difficult and distorts line spacing to put mathematically appropriate bars over line segments \((\overline{\mathrm{AB}})\), arrows over rays \((\overline{\mathrm{AB}}\) or \(\overleftarrow{\mathrm{BA}})\), double-headed arrows over lines \((\overleftrightarrow{\mathrm{AB}})\), and arcs over arcs \((\overparen{\mathrm{AB}})\) when indicated by two points, usually uppercase English letters. USE THEM in your work consistently and correctly. Also be careful about "corresponding order". For example, in the above, we would have no reason to suspect that \(\triangle \mathrm{ABC} \cong \triangle \mathrm{FEG}\) but \(\triangle \mathrm{ABC} \cong \triangle \mathrm{EFG}\) is equivalent to the original. Note: As mentioned above, this is now a (universal) conditional statement or implication (i.e., if... then...), but often they are not so stated in mathematics. You should be able to effortlessly make the translation into an equivalent statement that does have that form and recognize universality when that is implied.

An artificial feature you might be used to is so-called "T-proof"; statements carefully matched with corresponding reasons why the statements are true in the context of the proof. If you feel more comfortable with such, feel free to use the structure but it is really just a pedagogical technique to convince beginning mathematics students that if a statement is made without a supporting reason (it could be understood but not explicitly stated), it is not a proof. True? Perhaps, but not proved.

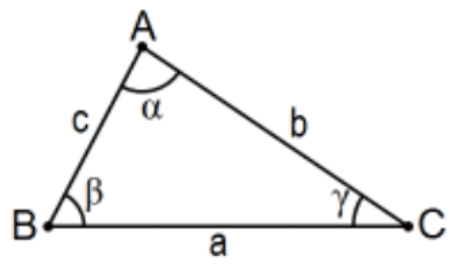
Another detail that will be used, and you are encouraged to use as well, is standard notation, some of which is mandatory and some of which is only preferred. (That preference may or may not be standard outside of the US). Points will be indicated by uppercase English letters and the vertices of a polygon must be listed in sequential order (clockwise or counterclockwise).

Likewise, corresponding vertices of corresponding polygons (usually congruent or similar but not necessarily) must be listed in corresponding order. A variable written inside of an angle indicates the measure of the angle - i.e., its angle size - not a name for the angle itself so do NOT indicate an angle by using its size instead of its name, several angles may have the same size but, obviously, different names.

A convenient convention, but far from standard, is to use the corresponding lowercase Greek letter for the measure of an angle of the same English name. That is, \(\mathrm{m}(\angle \mathrm{A})\) will often be indicated by \(\alpha, \mathrm{m}(\angle \mathrm{B})\) by \(\beta\), \(\mathrm{m}(\angle \mathrm{C})\) by \(\gamma\) (because it is next in the Greek alphabet), etc., and to use lowercase English letters to indicate the measure of a side and will often be the same letter (but lowercase) of the opposite vertex. Geometer’s Sketchpad automatically "fills in" angle measure indicators. Do NOT do that in your work; it is not standard usage. Another comment on usage, geometric entities such as angles, line segments, and polygons that are (informally speaking) the same size and shape are said to be congruent, as opposed to "equal", but measures \((\alpha, \beta, \mathrm{a}, \mathrm{b}\), etc.) are real numbers so, if they are the same, the appropriate word is "equal". This care with words (not shared by all geometers) comes from their underlying nature as sets of points. Sets are equal if and only if they have the same elements so consistency requires that, for example, \(\angle \mathrm{A}=\angle \mathrm{B}\) would imply that the two angles (union of two rays with a common initial point) were exactly the same two rays, not two angles of the same size that was probably the intent; instead express it symbolically as \(\angle A \cong \angle B\) and read that as "angle \(A\) is congruent to angle \(B\) ".

To get a feel as to how this formal/informal proof is to work, below are items from a generic first quiz along with suggested solutions (that look very much like the items of Problem Set 1 , hereafter PS 1). The instructions began simply with, "All items relate to the given isosceles triangle \(\triangle \mathrm{ABC}\)." Implied, of course, is what isosceles means, even triangle itself. There are lots of such "familiar" terms that are used herein and throughout the course, terms such as "is perpendicular to", "ray", "angle bisector", ASA, and SSS. Hopefully, these ideas are not new, although they will be reviewed. One that we will use that is common but not universal is "cpctc", "corresponding parts of congruent triangles are congruent". Equivalently, one might say "by congruence of triangles" (or of congruent geometric figures more generally) but cpctc is so handy and so commonly used that I encourage its use. Again, make yourself an accurate glossary of terms about which you have any doubt (after asking if there is anything about which you are unsure).

All items relate to the given isosceles triangle \(\triangle \mathrm{ABC}\) with base angles at \(B\) and \(\mathrm{C}\).

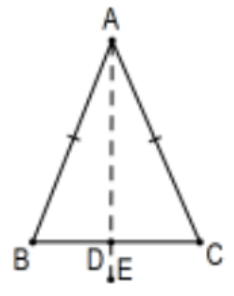
1. Indicate in the sketch all given information in the standard way. Equally importantly, indicate nothing but the given information.

Solution: Add matching congruence marks, "tick-marks" to segments \(A B\) and \(A C\).

2. Assume that point \(D\) is the point determined by the bisector of \(\angle A\). Prove that \(\angle B \cong \angle C\).

Solution: \(\mathrm{AB} \cong \mathrm{AC}\) by definition of isosceles (or "given") and \(\angle \mathrm{BAD} \cong \angle \mathrm{CAD}\) by definition of angle bisector (or "given"). Therefore, \(\triangle \mathrm{BAD} \cong \triangle \mathrm{CAD}\) by SAS and \(\angle \mathrm{B} \cong \angle \mathrm{C}\) by cpctc. [Note: What happened to \(\mathrm{AD} \cong \mathrm{AD}\) needed for \(\mathrm{SAS}\) ? Formally, it is the reflexive property of congruence but don’t bother. Isn’t it obviously true?!]

3. Assume that point \(\mathrm{D}\) is the midpoint of line segment \(B C\). Prove that \(\angle B \cong \angle C\).

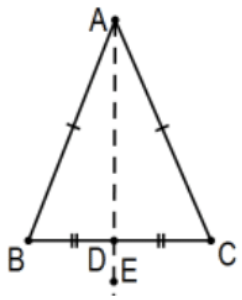
Solution: \(\mathrm{AB} \cong \mathrm{AC}\) by definition and \(\mathrm{BD} \cong \mathrm{CD}\) by definition of midpoint (or "given"). Therefore, \(\triangle \mathrm{BAD} \cong \triangle \mathrm{CAD}\) by \(\mathrm{SSS}\) and \(\angle \mathrm{B} \cong \angle \mathrm{C}\) by cpctc.

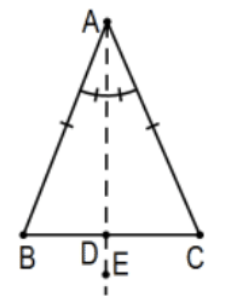
4. Assume that line DE is the perpendicular bisector of line segment BC. Don’t prove anything but explain why an easy hypotenuse-leg "proof" that \(\angle \mathrm{B} \cong \angle \mathrm{C}\) is fallacious.

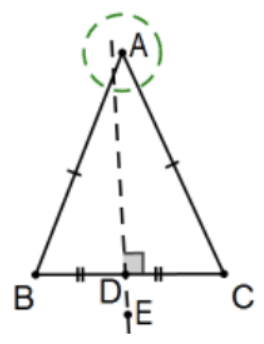
Answer: For all we know at this point, point A need not be on line DE.
(The circle at vertex A shows how the figure can be drawn to emphasize this.) That is, the "proof" assumes that \(\mathrm{A} \in \mathrm{DE}\) without first proving that fact.

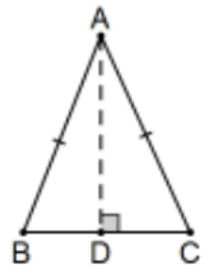
Valid Proof: Assume that \(\mathrm{D}\) is the foot of the perpendicular from \(A\) to line \(B C\) (i.e., no tick-marks that \(B D \cong C D)\). Now, by Hyp-Leg, \(\triangle \mathrm{ABD} \cong \triangle \mathrm{ACD}\) and \(\angle \mathrm{B} \cong \angle \mathrm{C}\) by cpctc.

Note: The problem of #4 is a very important idea. Once an entity is determined (and the perpendicular bisector of a line segment completely determines the line) all other properties about it must be proved or the situation is "over-determined"; i.e., information is being assumed without proof and might possibly even be false. That’s about as bad as it gets in "proof". In fact, it is better to say "I have no idea how to prove this."

5. Only using \(\triangle \mathrm{ABC}\) (that is, with no auxiliary points or lines), prove \(\angle \mathrm{B} \cong \angle \mathrm{C}\).

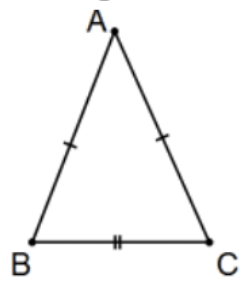
Solution: \(\mathrm{AB} \cong \mathrm{AC}\) by definition and \(\mathrm{BC} \cong \mathrm{CB}\). Therefore, \(\triangle \mathrm{BAC} \cong \triangle \mathrm{CAB}\) by \(\mathrm{SSS}\) and \(\angle B \cong \angle C\) by cpctc. [That is, the triangle is congruent to itself using a different correspondence.] Since \(\angle \mathrm{BAC} \cong \angle \mathrm{CAB}, \triangle \mathrm{BAC} \cong \triangle \mathrm{CAB}\) by \(\mathrm{SAS}\) as well.

Note: The two proofs of #5 are a bit more subtle than they look. Congruence of geometric figures, in our interpretation, has been assumed to be in its "pure geometry" form; i.e., as an undefined term subject to some (albeit, unstated) axioms. For example, congruence is (among other things) an equivalence relation; i.e., it is reflexive, symmetric, and transitive. More explicitly:

i. Figure \(\mathrm{F}\) is congruent to Figure \(\mathrm{F}\),

ii. If Figure \(\mathrm{F}\) is congruent to Figure \(\mathrm{G}\), then Figure \(\mathrm{G}\) is congruent to Figure \(\mathrm{F}\), and

iii. If Figure \(\mathrm{F}\) is congruent to Figure \(\mathrm{G}\) and Figure \(\mathrm{G}\) is congruent to Figure \(\mathrm{H}\), then Figure \(\mathrm{F}\) is congruent to Figure H.

In the \(\mathrm{SSS}\) proof, we assumed \(\mathrm{BC} \cong \mathrm{CB}\) without proof and your instinct (perhaps past teaching?) would call that true by the reflexive property of congruence. It is not, however, because the orientation is reversed. A less "pure" form of geometry (e.g., including the Ruler and Protractor Postulates as we do) defines congruence, and not among specific geometric figures, but of the entire point set of the geometry. Formally, in this context, a congruence would be defined to be a one-to-one correspondence of the entire plane that preserves the distance (unsigned measure) between any two corresponding points and the size of any two corresponding angles. For example, \(\mathrm{BC} \cong \mathrm{CB}\) because reflection in the perpendicular bisector of segment \(\mathrm{BC}\) is a congruence that carries segment \(\mathrm{BC}\) onto segment \(\mathrm{CB}\) including the entire triangle in question onto itself but with a new correspondence. Similarly for the SAS proof, reflection in the line of the bisector of angle \(\angle \mathrm{BAC}\) is the needed congruence. Another congruence that you are probably familiar with is rotation about a single point and all compositions of these two. In Euclidean geometry, translation by a vector (a directed line segment) is another, sometimes called a "glide" in elementary books. Are there others? The answer is "no" but we will not prove that fact in this course.

Except for translations (that need unique parallels), these are also congruences in neutral (or absolute) geometry; that is, without reference to Euclid’s \(5^{\text {th }}\) Postulate that gives us Euclidean geometry so these statements are true in both Euclidean and hyperbolic geometry even though we may be "thinking" Euclidean geometry only (and still have no idea what hyperbolic geometry might be!).

One last complexity that is often overlooked in introductory geometry classes is that, for independence of the axioms, the congruence statements (i.e., SAS, SSS, ASA, AAS, and Hypotenuse-Leg) are not "axioms", at least not most of them. Although the Greeks did not realize it, one of these (or something equivalent) must be taken as an axiom and the rest are theorems, conditional statements to be proved.

That last statement is not quite true but almost. For example, in Hilbert’s axioms, congruence of segments and angles are described axiomatically and congruence of geometric figures (restricted to connected ones consisting of segments and angles) are then defined to be congruent if there is a one-to-one correspondence of their points such that all segments and angles correspond and are congruent. With this restriction, his basic axiom is not quite \(\mathrm{SAS}\); it includes congruence of the missing two angles but omits congruence of the missing side and proves the full SAS as a theorem. That is so close as to be almost trivial except for the idea of keeping the set of axioms at the absolute minimum needed. [See Hilbert’s classic 1902 book, Foundations of Geometry, Open Court Publishing Co., Axiom IV, 6 and Theorem 10.]

We will take SAS as an axiom and use it to prove the others although, for example, sSS could be used instead. Although SSS will be stated independently, it really is, "If SAS, then SSS". In terms of formal logic (and ignoring the understood universal nature of the situation); i.e., "For every...", before the antecedent and again before the consequent in the implication, "If \((p \Rightarrow q)\), then \((r \Rightarrow s)\) ", or fully, " \((p \Rightarrow q) \Rightarrow(r \Rightarrow s)\) ". In such a situation, we simply assume the truth of the statement \(r\) and somehow prove that the statement \(s\) must also be true. In the process of proving \(s\), it would be expected that somewhere along the line, maybe several times, the assumed truth of any occurrence of \(p \Rightarrow q\) would be used.

In fact, it is more complicated than that. In reality, it says that "If all of the axioms of neutral geometry including SAS and previously proved theorems are true, then SSS, is also true." More generally, throughout formal mathematics, that is the idea: A large collection of "stuff" is used to prove some new conditional statement. None of that complicated antecedent is mentioned, only the antecedent of the new conditional statement that is to be proved. As mentioned above, we could just as well assume \(S S S\) as our axiom and use it to prove SAS. Focusing just on the congruence concepts, that makes the conditional statement "If SSS, then SAS" the converse of "If SAS, then SSS." In that case, were we to prove the statement, we would simply say, "Prove SAS." To do that, we would have to discard any statements we thought were true because they had been proved using SAS, and somehow build a proof using SSS to prove that the two triangles with the SAS hypothesis are, in fact, congruent. That is we start with two triangles that satisfy the hypotheses of SAS (NOT the hypothesis of \(\mathrm{SSS}\) ) and prove that the triangles are congruent. To do this, the setup could look exactly as the SAS that we looked at before:

Given: \(\overline{\mathrm{AB}} \cong \overline{\mathrm{EF}}, \overline{\mathrm{AC}} \cong \overline{\mathrm{EG}}\), and \(\angle \mathrm{A} \cong \angle \mathrm{E}\) (or \(\angle \mathrm{BAC} \cong \angle \mathrm{FEG})\)

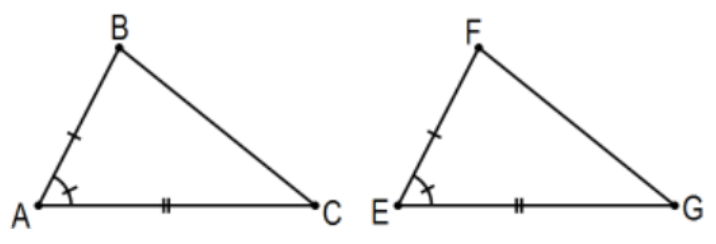
Conclusion: \(\triangle \mathrm{BAC} \cong \triangle \mathrm{FEG}\).

Where is the SSS? Whenever and wherever we have the conditions of SSS for two triangles (not these two(!), at least not yet), we are to conclude that those triangles are congruent. To prove the result, we need to somehow build triangles that do satisfy the conditions of SSS as a bridge to proving that these two are also congruent. How to do that may or may not be easy depending on one’s experience and mathematical creativity. Whatever we do, however, we must be careful not to use any theorems that were proved using SAS or we have clear, albeit unintentional, circular reasoning. At this stage that is easy to do since we haven’t proved any theorems except for the congruence of the base angles of isosceles triangles and we did offer a SSS proof for that fact (which we don’t need anyway). To see how this could work, we introduce another familiar concept:

The allowed "tools" are an unmarked straightedge (a realization of Axiom 1) and a compass (a realization of "knowing" a circle given a point for a center and a line segment or its length for a radius). These are often called the "Euclidean tools" but (since they are artificial realizations of the abstract consequence of the axioms of neutral geometry) they are assumed to be available throughout the course, Euclidean geometry or not. New points, lines, etc., identified because of them will be said to exist "by construction".

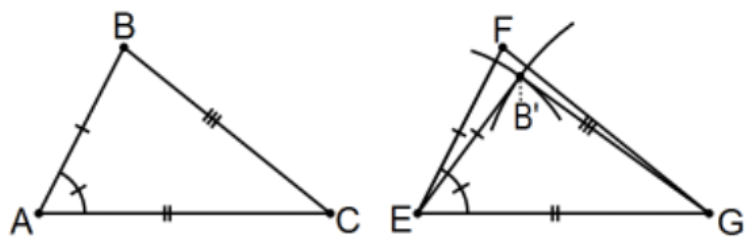
Proof: Construct point \(\mathrm{B}^{\prime}\) as the appropriate intersection of (E; AB), the circle with center at \(\mathrm{E}\) of radius \(\mathrm{AB}\), and (G; CB), the circle with center at \(G\) of radius CB. Now we have a new triangle with \(\triangle \mathrm{EB}^{\prime} \mathrm{G} \cong \triangle \mathrm{ABC}\) by SSS since we have three pairs of congruent sides "by construction". Now \(\angle B^{\prime} E G \cong \angle B A C\) because corresponding parts of congruent triangles are congruent (cpctc). By hypothesis, \(\angle B A C \cong \angle F E G\) so, by transitivity of congruence, \(\angle B^{\prime} E G \cong \angle F E G\). By the Protractor Postulate, ray \(\mathrm{EB}^{\prime}\) and ray \(E F\) are exactly the same ray. Moreover, \(\mathrm{EB}^{\prime} \cong A B\) by construction and it was given that \(\mathrm{AB} \cong \mathrm{EF}\) so, by transitivity, \(\mathrm{EB}^{\prime} \cong \mathrm{EF}\) so, by the Ruler Postulate, \(F\) and \(\mathrm{B}^{\prime}\) are exactly the same point \(\left(F=B^{\prime}\right)\). Therefore, the original triangles are congruent because we already knew that they were congruent, we just have another name for one of the points. QED.

For more on the issue, see Ex 22 at the end of Problem Set 1 (hereafter indicated PS 1, #22).