4.6: Multiplying and Dividing Mixed Fractions
- Page ID
- 22484
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We begin with definitions of proper and improper fractions.
A proper fraction is a fraction whose numerator is smaller than its denominator. An improper fraction is a fraction whose numerator is larger than its denominator.
For example,
\[ \frac{2}{3}, ~ - \frac{23}{39}, \text{ and } \frac{ 119}{127}\nonumber \]
are all examples of proper fractions. On the other hand,
\[ \frac{4}{3},~ - \frac{317}{123}, \text{ and } - \frac{233}{101}\nonumber \]
are all examples of improper fractions.
A mixed fraction1 is part whole number, part fraction.
The number
\[ 5 \frac{3}{4}\nonumber \]
is called a mixed fraction. It is defined to mean
\[5 \frac{3}{4} = 5 + \frac{3}{4}.\nonumber \]
In the mixed fraction \(5 \frac{3}{4}\), the 5 is the whole number part and the 3/4 is the fractional part.
Changing Mixed Fractions to Improper Fractions
We have all the tools required to change a mixed fraction into an improper fraction. We begin with an example.
Change the mixed fraction \(4 \frac{7}{8}\) into an improper fraction.
Solution
We employ the definition of a mixed fraction, make an equivalent fraction for the whole number part, then add.
\[ \begin{aligned} 4 \frac{7}{8} = 4 + \frac{7}{8} ~ & \textcolor{red}{ \text{ By definition.}} \\ = \frac{4 \cdot \textcolor{red}{8}}{ \textcolor{red}{8}} + \frac{7}{8} ~ & \textcolor{red}{ \text{ Equivalent fraction with LCD = 8.}} \\ = \frac{4 \cdot 8 + 7}{8} ~ & \textcolor{red}{ \text{ Add numerators over common denominator.}} \\ = \frac{39}{8} ~ & \textcolor{red}{ \text{ Simplify the numerator.}} \end{aligned}\nonumber \]
Thus, \(4 \frac{7}{8}\) is equal to 39/8.
Change \(5 \frac{3}{4}\) to an improper fraction.
- Answer
-
23/4
There is a quick technique you can use to change a mixed fraction into an improper fraction.
To change a mixed fraction to an improper fraction, multiply the whole number part by the denominator, add the numerator, then place the result over the denominator.
Thus, to quickly change \(4 \frac{7}{8}\) to an improper fraction, multiply the whole number 4 by the denominator 8, add the numerator 7, then place the result over the denominator. In symbols, this would look like this:
\[ 4 \frac{7}{8} = \frac{4 \cdot 8 + 7}{8}.\nonumber \]
This is precisely what the third step in Example 1 looks like; we’re just eliminating a lot of the work.
Change \(4 \frac{2}{3}\) to an improper fraction.
Solution
Take \(4 \frac{2}{3}\), multiply the whole number part by the denominator, add the numerator, then put the result over the denominator.
\[4 \frac{2}{3} = \frac{4 \cdot 3 + 2}{3}\nonumber \]
Thus, the result is
\[4 \frac{2}{3} = \frac{14}{3}.\nonumber \]
Change \(7 \frac{3{8}\) to an improper fraction.
- Answer
-
59/8
It is very easy to do the intermediate step in Example 2 mentally, allowing you to skip the intermediate step and go directly from the mixed fraction to the improper fraction without writing down a single bit of work.
Without writing down any work, use mental arithmetic to change \(-2 \frac{3}{5}\) to an improper fraction.
Solution
To change \(−2 \frac{3}{5}\) to an improper fraction, ignore the minus sign, proceed as before, then prefix the minus sign to the resulting improper fraction. So, multiply 5 times 2 and add 3. Put the result 13 over the denominator 5, then prefix the resulting improper fraction with a minus sign. That is,
\[-2 \frac{3}{5} = - \frac{13}{5}.\nonumber \]
Change \(-3 \frac{5}{12}\) to an improper fraction.
- Answer
-
−41/12
Changing Improper Fractions to Mixed Fractions
The first step in changing the improper fraction 27/5 to a mixed fraction is to write the improper fraction as a sum.
\[\frac{27}{5} = \frac{25}{5} + \frac{2}{5}\nonumber \]
Simplifying equation 4.1, we get
\[ \begin{aligned} \frac{27}{5} = 5 + \frac{2}{5} \\ = 5 \frac{2}{5} \end{aligned}\nonumber \]
Comment. You can’t just choose any sum. The sum used in equation 4.1 is constructed so that the first fraction will equal a whole number and the second fraction is proper. Any other sum will fail to produce the correct mixed fraction. For example, the sum
\[ \frac{27}{5} = \frac{23}{5} + \frac{4}{5}\nonumber \]
is useless, because 23/5 is not a whole number. Likewise, the sum
\[ \frac{27}{5} = \frac{20}{5} + \frac{7}{5}\nonumber \]
is no good. Even though 20/5 = 4 is a whole number, the second fraction 7/5 is still improper.
Change 25/9 to a mixed fraction.
Solution
Break 25/9 into the appropriate sum.
\[ \begin{aligned} \frac{25}{9} = \frac{18}{9} + \frac{7}{9} \\ = 2 + \frac{7}{9} \\ = 2 \frac{7}{9} \end{aligned}\nonumber \]
Change 25/7 to a mixed fraction.
- Answer
-
\(3 \frac{4}{7}\).
Comment. A pattern is emerging. • In the case of 27/5, note that 27 divided by 5 is equal to 5 with a remainder of 2. Compare this with the mixed fraction result: 27/5=5 2 5 . • In the case of Example 4, note that 25 divided by 9 is 2 with a remainder of 7. Compare this with the mixed fraction result: 25/9=2 7 9 . These observations motivate the following technique.
To change an improper fraction to a mixed fraction, divide the numerator by the denominator. The quotient will be the whole number part of the mixed fraction. If you place the remainder over the denominator, this will be the fractional part of the mixed fraction.
Change 37/8 to a mixed fraction.
Solution
37 divided by 8 is 4, with a remainder of 5. That is:
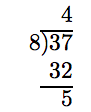
The quotient becomes the whole number part and we put the remainder over the divisor. Thus,
\[ \frac{37}{8} = 4 \frac{5}{8}.\nonumber \]
Note: You can check your result with the “Quick Way to Change a Mixed Fraction to an Improper Fraction.” 8 times 4 plus 5 is 37. Put this over 8 to get 37/8.
Change 38/9 to a mixed fraction.
- Answer
-
\(4 \frac{2}{9}\)
Change −43/5 to a mixed fraction.
Solution
Ignore the minus sign and proceed in the same manner as in Example 5. 43 divided by 5 is 8, with a remainder of 3.
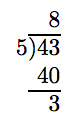
The quotient is the whole number part, then we put the remainder over the divisor. Finally, prefix the minus sign.
\[ -\frac{43}{5} = -8 \frac{3}{5}\nonumber \]
Multiplying and Dividing Mixed Fractions
You have all the tools needed to multiply and divide mixed fractions. First, change the mixed fractions to improper fractions, then multiply or divide as you did in previous sections.
1A mixed fraction is sometimes called a mixed number.
Simplify: \(-2 \frac{1}{12} \cdot 2 \frac{4}{5}\).
Solution
Change to improper fractions, factor, cancel, and simplify.
\[ \begin{aligned} -2 \frac{1}{12} \cdot 2 \frac{4}{5} = - \frac{25}{12} \cdot \frac{14}{5} ~ & \textcolor{red}{ \text{ Change to improper fractions.}} \\ = - \frac{25 \cdot 14}{12 \cdot 5} ~ & \textcolor{red}{ \begin{aligned} \text{ Multiply numerators; multiply denominators.} \\ \text{ Unlike signs; product is negative.} \end{aligned}} \\ = - \frac{(5 \cdot 5) \cdot (2 \cdot 7)}{2 \cdot 2 \cdot 3) \cdot (5)} ~ & \textcolor{red}{ \text{ Prime factor.}} \\ = - \frac{ \cancel{5} \cdot 5 \cdot \cancel{2} \cdot 7}{ \cancel{2} \cdot 2 \cdot 3 \cdot \cancel{5}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = - \frac{35}{6} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \end{aligned}\nonumber \]
This is a perfectly good answer, but if you want a mixed fraction answer, 35 divided by 6 is 5, with a remainder of 5. Hence,
\[ -2 \frac{1}{12} \cdot 2 \frac{4}{5} = -5 \frac{5}{6}.\nonumber \]
Simplify:
\[-3 \frac{3}{4} \cdot 2 \frac{2}{5}\nonumber \]
- Answer
-
−9
Simplify:
\[-4 \frac{4}{5} \div 5 \frac{3}{5}.\nonumber \]
Solution
Change to improper fractions, invert and multiply, factor, cancel, and simplify.
\[ \begin{aligned} -4 \frac{4}{5} \div 5 \frac{3}{5} = - \frac{24}{5} \div \frac{28}{5} ~ & \textcolor{red}{ \text{ Change to improper fractions.}} \\ = - \frac{24}{5} \cdot \frac{5}{28} ~ & \textcolor{red}{ \text{ Invert and multiply.}} \\ = - \frac{2 \cdot 2 \cdot 2 \cdot 3}{5} \cdot \frac{5}{2 \cdot 2 \cdot 7} ~ & \textcolor{red}{ \text{ Prime factor.}} \\ = - \frac{ \cancel{2} \cdot \cancel{2} \cdot 2 \cdot 3}{ \cancel{3}} \cdot \frac{ \cancel{5}}{ \cancel{2} \cdot \cancel{2} \cdot 7} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = - \frac{6}{7} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \cdot \end{aligned}\nonumber \]
Simplify:
\[-2 \frac{4}{9} \cdot 3 \frac{2}{3}\nonumber \]
- Answer
-
−2/3
Exercises
In Exercises 1-12, convert the mixed fraction to an improper fraction.
1. \(2 \frac{1}{3}\)
2. \(1 \frac{8}{11}\)
3. \(1 \frac{1}{19}\)
4. \(−1 \frac{1}{5}\)
5. \(−1 \frac{3}{7}\)
6. \(1 \frac{3}{17}\)
7. \(1 \frac{1}{9}\)
8. \(1 \frac{5}{11}\)
9. \(−1 \frac{1}{2}\)
10. \(−1 \frac{5}{8}\)
11. \(1 \frac{1}{3}\)
12. \(−1 \frac{5}{7}\)
In Exercises 13-24, convert the improper fraction to a mixed fraction.
13. \(\frac{13}{7}\)
14. \(\frac{−17}{9}\)
15. \(\frac{−13}{5}\)
16. \(\frac{−10}{3}\)
17. \(\frac{−16}{5}\)
18. \(\frac{16}{13}\)
19. \(\frac{9}{8}\)
20. \(\frac{16}{5}\)
21. \(\frac{−6}{5}\)
22. \(\frac{−17}{10}\)
23. \(\frac{−3}{2}\)
24. \(\frac{−7}{4}\)
In Exercises 25-48, multiply the numbers and express your answer as a mixed fraction.
25. \(1 \frac{1}{7} \cdot 2 \frac{1}{2}\)
26. \(1 \frac{1}{8} \cdot 1 \frac{1}{6}\)
27. \(4 \cdot 1 \frac{1}{6}\)
28. \(1 \frac{7}{10} \cdot 4\)
29. \( \left( −1 \frac{1}{12} \right) \left( 3 \frac{3}{4} \right)\)
30. \( \left( −3 \frac{1}{2} \right) \left( 3 \frac{1}{3} \right)\)
31. \(7 \frac{1}{2} \cdot 1 \frac{1}{13}\)
32. \(2 \frac{1}{4} \cdot 1 \frac{5}{11}\)
33. \( \left( 1 \frac{2}{13} \right) \left( −4 \frac{2}{3} \right)\)
34. \( \left( 1 \frac{1}{14} \right) \left( −2 \frac{2}{5} \right)\)
35. \( \left( 1 \frac{3}{7} \right) \left( −3 \frac{3}{4} \right)\)
36. \( \left( 1 \frac{4}{5} \right) \left( −3 \frac{3}{4} \right)\)
37. \(9 \cdot \left( −1 \frac{2}{15} \right)\)
38. \(4 \cdot \left( −2 \frac{5}{6} \right)\)
39. \( \left( −2 \frac{1}{8} \right) (−6)\)
40. \((−9) \left( −3 \frac{1}{6} \right)\)
41. \( \left( −4 \frac{1}{2} \right) \left( −2 \frac{2}{5} \right)\)
42. \( \left( −1 \frac{3}{7} \right) \left( −3 \frac{3}{4} \right)\)
43. \( \left( −2 \frac{1}{6} \right) \cdot 4\)
44. \((−6) \cdot \left( 1 \frac{1}{9} \right)\)
45. \( \left( −1 \frac{4}{15} \right) \left( 2 \frac{1}{2} \right)\)
46. \( \left( −1 \frac{1}{5} \right) \left( 1 \frac{5}{9} \right)\)
47. \( \left( −2 \frac{1}{2} \right) \left( −1 \frac{7}{11} \right)\)
48. \( \left( −1 \frac{7}{11} \right) \left( −1 \frac{7}{12} \right)\)
In Exercises 49-72, divide the mixed fractions and express your answer as a mixed fraction.
49. \(8 \div 2 \frac{2}{9}\)
50. \(4 \frac{2}{3} \div 4\)
51. \( \left( −3 \frac{1}{2} \right) \div \left( 1 \frac{1}{16} \right)\)
52. \( \left( −1 \frac{2}{5} \right) \div \left( 1 \frac{1}{15} \right)\)
53. \(6 \frac{1}{2} \div 1 \frac{7}{12}\)
54. \(5 \frac{1}{2} \div 1 \frac{9}{10}\)
55. \((−4) \div \left( 1 \frac{5}{9} \right)\)
56. \( \left( −4 \frac{2}{3} \right) \div 4\)
57. \( \left( −5 \frac{2}{3} \right) \div \left( −2 \frac{1}{6} \right)\)
58. \( \left( −2 \frac{1}{2} \right) \div \left( −2 \frac{2}{9} \right)\)
59. \( \left( −6 \frac{1}{2} \right) \div \left( 4 \frac{1}{4} \right)\)
60. \( \left( −1 \frac{1}{6} \right) \div \left( 1 \frac{1}{8} \right)\)
61. \((−6) \div \left( −1 \frac{3}{11} \right)\)
62. \( \left( −6 \frac{2}{3} \right) \div (−6)\)
63. \( \left( 4 \frac{2}{3} \right) \div (−4)\)
64. \( \left( 6 \frac{2}{3} \right) \div (−6)\)
65. \( \left( 1 \frac{3}{4} \right) \div \left( −1 \frac{1}{12} \right)\)
66. \( \left( 2 \frac{4}{7} \right) \div \left( −1 \frac{1}{5} \right)\)
67. \( \left( 5 \frac{2}{3} \right) \div 1 \frac{1}{9}\)
68. \( 1 \frac{2}{3} \div 1 \frac{2}{9}\)
69. \( \left( −7 \frac{1}{2} \right) \div \left( −2 \frac{2}{5} \right)\)
70. \( \left( −5 \frac{1}{3} \right) \div \left( −2 \frac{5}{6} \right)\)
71. \( \left( 3 \frac{2}{3} \right) \div \left( −1 \frac{1}{9} \right)\)
72. \( \left( 8 \frac{1}{2} \right) \div \left( −1 \frac{3}{4} \right)\)
73. Small Lots. How many quarter-acre lots can be made from \(6 \frac{1}{2}\) acres of land?
74. Big Field. A field was formed from \(17 \frac{1}{2}\) half-acre lots. How many acres was the resulting field ?
75. Jewelry. To make some jewelry, a bar of silver \(4 \frac{1}{2}\) inches long was cut into pieces \( \frac{1}{12}\) inch long. How many pieces were made?
76. Muffins. This recipe will make 6 muffins: 1 cup milk, \(1 \frac{2}{3}\) cups flour, 2 eggs, 1/2 teaspoon salt, \(1 \frac{1}{2}\) teaspoons baking powder. Write the recipe for six dozen muffins.
Answers
1. \( \frac{7}{3}\)
3. \( \frac{20}{19}\)
5. \(− \frac{10}{7}\)
7. \( \frac{10}{9}\)
9. \(− \frac{3}{2}\)
11. \( \frac{4}{3}\)
13. \(1 \frac{6}{7}\)
15. \(−2 \frac{3}{5}\)
17. \(−3 \frac{1}{5}\)
19. \(1 \frac{1}{8}\)
21. \(−1 \frac{1}{5}\)
23. \(−1 \frac{1}{2}\)
25. \(2 \frac{6}{7}\)
27. \(4 \frac{2}{3}\)
29. \(−4 \frac{1}{16}\)
31. \(8 \frac{1}{13}\)
33. \(−5 \frac{5}{13}\)
35. \(−5 \frac{5}{14}\)
37. \(−10 \frac{1}{5}\)
39. \(12 \frac{3}{4}\)
41. \(10 \frac{4}{5}\)
43. \(− 8 \frac{2}{3}\)
45. \(− 3 \frac{1}{6}\)
47. \(4 \frac{1}{11}\)
49. \(3 \frac{3}{5}\)
51. \(− 3 \frac{5}{17}\)
53. \(4 \frac{2}{19}\)
55. \(− 2 \frac{4}{7}\)
57. \(2 \frac{8}{13}\)
59. \(− 1 \frac{9}{17}\)
61. \(4 \frac{5}{7}\)
63. \(− 1 \frac{1}{6}\)
65. \(− 1 \frac{8}{13}\)
67. \(5 \frac{1}{10}\)
69. \(3 \frac{1}{8}\)
71. \(− 3 \frac{3}{10}\)
73. 26 quarter-acre lots
75. 54 pieces


