9.2: The Metric System of Measurement

Last updated
Save as PDF

Page ID: 48886

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

be more familiar with some of the advantages of the base ten number system
know the prefixes of the metric measures
be familiar with the metric system of measurement
be able to convert from one unit of measure in the metric system to another unit of measure

The Advantages of the Base Ten Number System

The metric system of measurement takes advantage of our base ten number system. The advantage of the metric system over the United States system is that in the metric system it is possible to convert from one unit of measure to another simply by multiplying or dividing the given number by a power of 10. This means we can make a conversion simply by moving the decimal point to the right or the left.

Prefixes

Common units of measure in the metric system are the meter (for length), the liter (for volume), and the gram (for mass). To each of the units can be attached a prefix. The metric prefixes along with their meaning are listed below.

Metric Prefixes

kilo: thousand
deci: tenth
hecto: hundred
centi: hundredth
deka: ten
milli: thousandth

For example, if length is being measured,

1 kilometer is equivalent to 1000 meters.
1 centimeter is equivalent to one hundredth of a meter.
1 millimeter is equivalent to one thousandth of a meter.

Conversion from One Unit to Another Unit

Let's note three characteristics of the metric system that occur in the metric table of measurements.

In each category, the prefixes are the same.
We can move from a larger to a smaller unit of measure by moving the decimal point to the right.
We can move from a smaller to a larger unit of measure by moving the decimal point to the left.

The following table provides a summary of the relationship between the basic unit of measure (meter, gram, liter) and each prefix, and how many places the decimal point is moved and in what direction.

kilo hecto deka unit deci centi milli

Basic Unit to Prefix		Move the Decimal Point
unit to deka	1 to 10	1 place to the left
unit to hector	1 to 100	2 places to the left
unit to kilo	1 to 1,000	3 places to the left
unit to deci	1 to 0.1	1 place to the right
unit to centi	1 to 0.01	2 places to the right
unit to milli	1 to 0.001	3 places to the right

Conversion Table

Listed below, in the unit conversion table, are some of the common metric units of measure.

Unit Conversion Table
Length	$\text{1 kilometer (km) = 1,000 meters } (m)$	$1,000 \times 1\text{m}$
	$\text{1 hectometer (hm) = 100 meters}$	$100 \times 1 \text{m}$
	$\text{1 dekameter (dam) = 10 meters}$	$10 \times 1 \text{m}$
	$\text{1 meter (m)}$	$1 \times 1 \text{m}$
	$\text{1 decimeter (dm) = } \dfrac{1}{10} \text{ meter}$	$.1 \times 1 \text{m}$
	$\text{1 centimeter (cm) = } \dfrac{1}{100} \text{ meter}$	$.01 \times 1 \text{m}$
	$\text{1 millimeter (mm) = } \dfrac{1}{1,000} \text{ meter}$	$.001 \times 1 \text{m}$
Mass	$\text{1 kilogram (kg) = 1,000 grams } (g)$	$1,000 \times 1\text{g}$
	$\text{1 hectogram (hg) = 100 grams}$	$100 \times 1 \text{g}$
	$\text{1 dekagram (dag) = 10 grams}$	$10 \times 1 \text{g}$
	$\text{1 gram (g)}$	$1 \times 1 \text{g}$
	$\text{1 decigram (dg) = } \dfrac{1}{10} \text{ gram}$	$.1 \times 1 \text{g}$
	$\text{1 centigram (cg) = } \dfrac{1}{100} \text{ gram}$	$.01 \times 1 \text{g}$
	$\text{1 milligram (mg) = } \dfrac{1}{1,000} \text{ gram}$	$.001 \times 1 \text{g}$
Volume	$\text{1 kiloliter (kL) = 1,000 liters } (L)$	$1,000 \times 1\text{L}$
	$\text{1 hectoliter (hL) = 100 liters}$	$100 \times 1 \text{L}$
	$\text{1 dekaliter (daL) = 10 liters}$	$10 \times 1 \text{L}$
	$\text{1 liter (L)}$	$1 \times 1 \text{L}$
	$\text{1 deciliter (dL) = } \dfrac{1}{10} \text{ liter}$	$.1 \times 1 \text{L}$
	$\text{1 centiliter (cL) = } \dfrac{1}{100} \text{ liter}$	$.01 \times 1 \text{L}$
	$\text{1 milliliter (mL) = } \dfrac{1}{1,000} \text{ liter}$	$.001 \times 1 \text{L}$
Time	Same as the United States system

Distinction Between Mass and Weight
There is a distinction between mass and weight. The weight of a body is related to gravity whereas the mass of a body is not. For example, your weight on the earth is different than it is on the moon, but your mass is the same in both places. Mass is a measure of a body's resistance to motion. The more massive a body, the more resistant it is to motion. Also, more massive bodies weigh more than less massive bodies.

Converting Metric Units
To convert from one metric unit to another metric unit:

Determine the location of the original number on the metric scale (pictured in each of the following examples).
Move the decimal point of the original number in the same direction and same number of places as is necessary to move to the metric unit you wish to go to.

We can also convert from one metric unit to another using unit fractions. Both methods are shown in Sample Set A.

Sample Set A

Convert 3 kilograms to grams.

Solution

a. 3 kg can be written as 3.0 kg. Then,
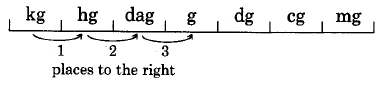
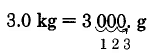
$A line with hash marks dividing the line into seven segments. The segments are labeled, from left to right, kg, hg, dag, g, dg, cg, and mg. Below kg, hg, dagga, and g are arrows pointing from each segment to the neighboring segment on the right. These arrows are labeled 1, 2, and 3, indicating the number of places to the right.$ $3.0 kg is equal to 3000g. An arrow is drawn under the three zeros in 3000, counting three decimal places to the right.$

Thus, $\text{3 kg = 3,000 g}$.

b. We can also use unit fractions to make this conversion.

Since we are converting to grams, and $\text{1,000 g = 1 kg}$. we choose the unit fraction $\dfrac{\text{1,000 g}}{\text{1 kg}}$ since grams is in the numerator.

$\begin{array} {rcl} {\text{3 kg}} & = & {\text{3 kg} \cdot \dfrac{\text{1,000 g}}{\text{1 kg}}} \\ {} & = & {3 \cancel{\text{kg}} \cdot \dfrac{\text{1,000 g}}{1 \cancel{\text{kg}}}} \\ {} & = & {3 \cdot 1,000 \text{ g}} \\ {} & = & {3,000 \text{ g}} \end{array}$

Sample Set A

Convert 67.2 hectoliters to milliliters.

Solution

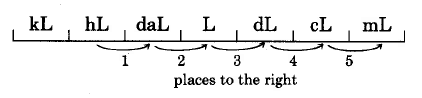
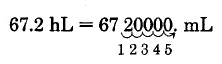
$A line with hash marks dividing the line into seven segments. The segments are labeled, from left to right, kL, hL, dal, L, dL, cL, and mL. Below hL, dal, L, dL, cL, and mL are arrows pointing from each segment to the neighboring segment on the right. These arrows are labeled 1 through 5 indicating the number of places to the right.$ $62.7 hL is equal to 6720000 mL. An arrow is drawn under the rightmost five digits in 6720000, counting five decimal places to the right.$

Thus, $\text{67.2 hL = 6,720,000 mL}$.

Sample Set A

Convert 100.07 centimeters to meters.

Solution

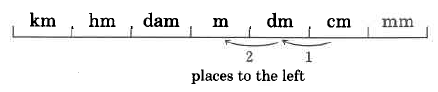
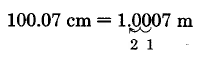
$A line with hash marks dividing the line into seven segments. The segments are labeled, from left to right, km, hm, dam, m, dm, cm, mm. Below cm, dm, and m are arrows pointing from each segment to the neighboring segment on the left. These arrows are labeled 1 and 2, indicating the number of places to the left.$ $100.07 cm equals 1.0007 m. Arrows under the two leftmost zeros are labeled 1 and 2, pointing to the left, indicating the number of decimal places moved.$

Thus, $\text{100.07 cm = 1.0007m}$.

Sample Set A

Convert 0.16 milligrams to grams.

Solution

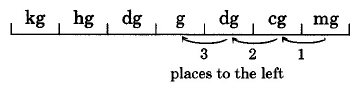
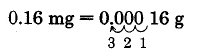
$A line with hash marks dividing the line into seven segments. The segments are labeled, from left to right, kg, hg, dg, g, dg, cg, and mg. Below g, dg, cg, and mg are arrows pointing from each segment to the neighboring segment on the left. These arrows are labeled 1, 2, and 3, indicating the number of places to the left.$ $0.16mg equals 0.00016g. Underneath the rightmost three zeros are arrows pointing to the left, labeled 1, 2, and 3, indicating the movement of the decimal point.$

Thus, $\text{0.16 mg = 0.00016}$.

Practice Set A

Convert 411 kilograms to grams.

Answer: 411,000 g

Practice Set A

Convert 5.626 liters to centiliters.

Answer: 562.6 cL

Practice Set A

Convert 80 milliliters to kiloliters.

Answer: 0.00008 kL

Practice Set A

Convert 150 milligrams to centigrams.

Answer: 15 cg

Practice Set A

Convert 2.5 centimeters to meters.

Answer: 0.025 m

Exercises

Make each conversion.

Exercise $\PageIndex{1}$

87 m to cm

Answer: 8,700 cm

Exercise $\PageIndex{2}$

905 L to mL

Exercise $\PageIndex{3}$

16,005 mg to g

Answer: 16.005 g

Exercise $\PageIndex{4}$

48.66 L to dL

Exercise $\PageIndex{5}$

11.161 kL to L

Answer: 11,161 L

Exercise $\PageIndex{6}$

521.85 cm to mm

Exercise $\PageIndex{7}$

1.26 dag to dg

Answer: 126 dg

Exercise $\PageIndex{8}$

99.04 dam to cm

Exercise $\PageIndex{9}$

0.51 kL to daL

Answer: 5.1 daL

Exercise $\PageIndex{10}$

0.17 kL to daL

Exercise $\PageIndex{11}$

0.05 m to dm

Answer: 0.5 dm

Exercise $\PageIndex{12}$

0.001 km to mm

Exercise $\PageIndex{13}$

8.106 hg to cg

Answer: 81,060 cg

Exercise $\PageIndex{14}$

17.0186 kL to mL

Exercise $\PageIndex{15}$

3 cm to m

Answer: 0.03 m

Exercise $\PageIndex{16}$

9 mm to m

Exercise $\PageIndex{17}$

4 g to mg

Answer: 4,000 mg

Exercise $\PageIndex{18}$

2 L to kL

Exercise $\PageIndex{19}$

6 kg to mg

Answer: 6,000,000 mg

Exercise $\PageIndex{20}$

7 daL to mL

Exercises for Review

Exercise $\PageIndex{21}$

Find the value of $\dfrac{5}{8} - \dfrac{1}{3} + \dfrac{3}{4}$

Answer: $\dfrac{25}{24} = 1 \dfrac{1}{24}$

Exercise $\PageIndex{22}$

Solve the proportion: $\dfrac{9}{x} = \dfrac{27}{60}$.

Exercise $\PageIndex{23}$

Use the method of rounding to estimate the sum: $8,226 + 4,118$.

Answer: 12,300 (12,344)

Exercise $\PageIndex{24}$

Use the clustering method to estimate the sum: $87 + 121 + 118 + 91 + 92$.

Exercise $\PageIndex{25}$

Convert 3 in. to yd.

Answer: $0.08\overline{3}$ yard.

Unit Conversion Table
Length	\(\text{1 kilometer (km) = 1,000 meters } (m)\)	\(1,000 \times 1\text{m}\)
	\(\text{1 hectometer (hm) = 100 meters}\)	\(100 \times 1 \text{m}\)
	\(\text{1 dekameter (dam) = 10 meters}\)	\(10 \times 1 \text{m}\)
	\(\text{1 meter (m)}\)	\(1 \times 1 \text{m}\)
	\(\text{1 decimeter (dm) = } \dfrac{1}{10} \text{ meter}\)	\(.1 \times 1 \text{m}\)
	\(\text{1 centimeter (cm) = } \dfrac{1}{100} \text{ meter}\)	\(.01 \times 1 \text{m}\)
	\(\text{1 millimeter (mm) = } \dfrac{1}{1,000} \text{ meter}\)	\(.001 \times 1 \text{m}\)
Mass	\(\text{1 kilogram (kg) = 1,000 grams } (g)\)	\(1,000 \times 1\text{g}\)
	\(\text{1 hectogram (hg) = 100 grams}\)	\(100 \times 1 \text{g}\)
	\(\text{1 dekagram (dag) = 10 grams}\)	\(10 \times 1 \text{g}\)
	\(\text{1 gram (g)}\)	\(1 \times 1 \text{g}\)
	\(\text{1 decigram (dg) = } \dfrac{1}{10} \text{ gram}\)	\(.1 \times 1 \text{g}\)
	\(\text{1 centigram (cg) = } \dfrac{1}{100} \text{ gram}\)	\(.01 \times 1 \text{g}\)
	\(\text{1 milligram (mg) = } \dfrac{1}{1,000} \text{ gram}\)	\(.001 \times 1 \text{g}\)
Volume	\(\text{1 kiloliter (kL) = 1,000 liters } (L)\)	\(1,000 \times 1\text{L}\)
	\(\text{1 hectoliter (hL) = 100 liters}\)	\(100 \times 1 \text{L}\)
	\(\text{1 dekaliter (daL) = 10 liters}\)	\(10 \times 1 \text{L}\)
	\(\text{1 liter (L)}\)	\(1 \times 1 \text{L}\)
	\(\text{1 deciliter (dL) = } \dfrac{1}{10} \text{ liter}\)	\(.1 \times 1 \text{L}\)
	\(\text{1 centiliter (cL) = } \dfrac{1}{100} \text{ liter}\)	\(.01 \times 1 \text{L}\)
	\(\text{1 milliliter (mL) = } \dfrac{1}{1,000} \text{ liter}\)	\(.001 \times 1 \text{L}\)
Time	Same as the United States system