1.1: Angles
- Page ID
- 3243
Recall the following definitions from elementary geometry:
- An angle is acute if it is between \(0°\) and \(90°\).
- An angle is a right angle if it equals \(90°\).
- An angle is obtuse if it is between \(90°\) and \(180°\).
- An angle is a straight angle if it equals \(180°\).

In elementary geometry, angles are always considered to be positive and not larger than \(360^\circ \). For now we will only consider such angles. The following definitions will be used throughout the text:
- Two acute angles are complementary if their sum equals \(90^◦\). In other words, if \(0^◦ ≤ ∠ A , ∠B ≤ 90^◦ \text{ then }∠ A \text{ and }∠B\) are complementary if \(∠ A +∠B = 90^◦\).
- Two angles between \(0^◦ \text{ and }180^◦\) are supplementary if their sum equals \(180^◦\). In other words, if \(0^◦ ≤ ∠ A , ∠B ≤ 180^◦ \text{ then }∠ A \text{ and }∠B\) are supplementary if \(∠ A +∠B = 180^◦\).
- Two angles between \(0^◦ \text{ and }360^◦\) are conjugate (or explementary) if their sum equals \(360^◦\). In other words, if \(0^◦ ≤ ∠ A , ∠B ≤ 360^◦ \text{ then }∠ A \text{ and }∠B\text{ are conjugate if }∠ A+∠B = 360^◦\).
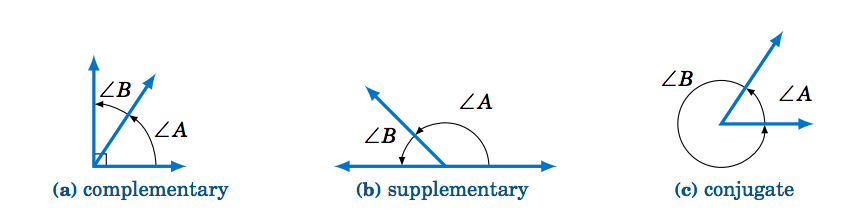
Instead of using the angle notation \(∠ A\) to denote an angle, we will sometimes use just a capital letter by itself (e.g. \(A, B, C\)) or a lowercase variable name (e.g. \(x, y, t\)). It is also common to use letters (either uppercase or lowercase) from the Greek alphabet, shown in the table below, to represent angles:
Table 1.1 The Greek alphabet

In elementary geometry you learned that the sum of the angles in a triangle equals \(180^◦\), and that an isosceles triangle is a triangle with two sides of equal length. Recall that in a right triangle one of the angles is a right angle. Thus, in a right triangle one of the angles is \(90^◦\) and the other two angles are acute angles whose sum is \(90^◦\) (i.e. the other two angles are complementary angles).
For each triangle below, determine the unknown angle(s):

Note: We will sometimes refer to the angles of a triangle by their vertex points. For example, in the first triangle above we will simply refer to the angle \(\angle\,BAC\) as angle \(A\).
Solution:
For triangle \(\triangle\,ABC\), \( A = 35^\circ\) and \(C = 20^\circ\), and we know that \(A + B + C = 180^\circ\), so
\[\nonumber 35^◦ + B + 20^◦ = 180^◦ ⇒ B = 180^◦ − 35^◦ − 20^◦ ⇒ \fbox{\(B = 125^◦\)} . \nonumber \]
For the right triangle \(△DEF,\, E = 53^◦ \text{ and }F = 90^◦\), and we know that the two acute angles \(D\) and \(E\) are complementary, so
\[\nonumber D + E = 90^◦ ⇒ D = 90^◦ − 53^◦ ⇒ \fbox{\(D = 37^◦\)} . \nonumber \]
For triangle \(△ XY Z\), the angles are in terms of an unknown number \(α\), but we do know that \(X +Y + Z = 180^◦\), which we can use to solve for \(α\) and then use that to solve for \(X, Y, \text{ and }Z\):
\[\nonumber α + 3α + α = 180^◦ ⇒ 5α = 180^◦ ⇒ α = 36^◦ ⇒ \fbox{\(X = 36^◦ ,\, Y = 3×36^◦ = 108^◦ ,\, Z = 36^◦\)} \nonumber \]
Thales' Theorem states that if \(A, \, B,\text{ and }C\) are (distinct) points on a circle such that the line segment \(\overline{AB}\) is a diameter of the circle, then the angle \(\angle\,ACB\) is a right angle (see Figure 1.1.3(a)). In other words, the triangle \(\triangle\,ABC\) is a right triangle.
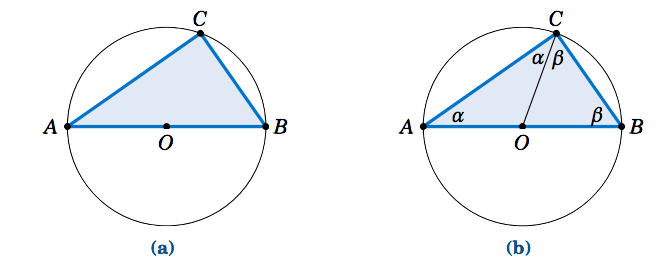
To prove this, let \(O\) be the center of the circle and draw the line segment \(\overline{OC}\), as in Figure 1.1.3(b). Let \(α = ∠BAC \text{ and }β = ∠ ABC\). Since \(\overline{AB}\) is a diameter of the circle, \(\overline{OA} \text{ and }\overline{OC}\) have the same length (namely, the circle’s radius). This means that \(△OAC \text{ is an isosceles triangle, and so }∠OCA = ∠OAC = α\). Likewise, \(△OBC\) is an isosceles triangle and \(∠OCB = ∠OBC = β\). So we see that \(∠ ACB = α+β\). And since the angles of \(△ ABC\) must add up to \(180^◦\), we see that \(180^◦ = α+(α+β)+β = 2 (α+β), \text{ so }α+β = 90^◦\). Thus, \(∠ ACB = 90^◦\). QED
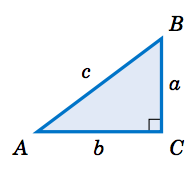
By knowing the lengths of two sides of a right triangle, the length of the third side can be determined by using the Pythagorean Theorem:
The square of the length of the hypotenuse of a right triangle is equal to the sum of the squares of the lengths of its legs.
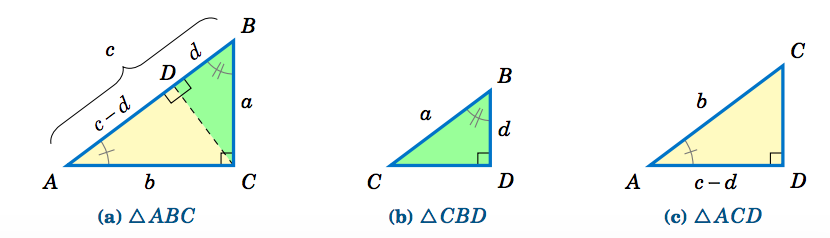
Recall that triangles are similar if their corresponding angles are equal, and that similarity implies that corresponding sides are proportional. Thus, since \(\triangle\,ABC \) is similar to \(\triangle\,CBD \), by proportionality of corresponding sides we see that
\[\nonumber \overline{AB}~\text{is to}~\overline{CB}~\text{(hypotenuses)}\text{ as }
\overline{BC}~\text{is to}~\overline{BD}~\text{(vertical legs)}
\quad\Rightarrow\quad \frac{c}{a} ~=~ \frac{a}{d} \quad\Rightarrow\quad cd ~=~ a^2 ~. \nonumber \]
Since \(\triangle\,ABC \) is similar to \(\triangle\,ACD \), comparing horizontal legs and hypotenuses gives
\[\nonumber \frac{b}{c-d} ~=~ \frac{c}{b} \quad\Rightarrow\quad b^2 ~=~ c^2 ~-~ cd ~=~ c ^2 ~-~ a^2
\quad\Rightarrow\quad a^2 ~+~ b^2 ~=~ c^2 ~. \textbf{QED} \nonumber \]
Note: The symbols \(\perp\) and \(\sim\) denote perpendicularity and similarity, respectively. For example, in the above proof we had \(\,\overline{CD} \perp \overline{AB}\, \) and \(\,\triangle\,ABC \sim \triangle\,CBD \sim \triangle\,ACD \).
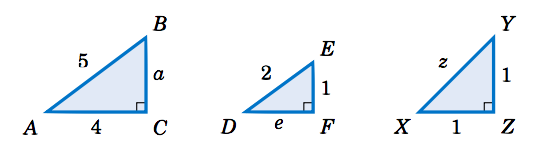
For each right triangle below, determine the length of the unknown side:
Solution:
For triangle \(\triangle\,ABC \), the Pythagorean Theorem says that
\[\nonumber a^2 ~+~ 4^2 ~=~ 5^2 \quad\Rightarrow\quad a^2 ~=~ 25 ~-~ 16 ~=~ 9 \quad\Rightarrow\quad
\fbox{\(a ~=~ 3\)} ~. \nonumber \]
For triangle \(\triangle\,DEF \), the Pythagorean Theorem says that
\[\nonumber e^2 ~+~ 1^2 ~=~ 2^2 \quad\Rightarrow\quad e^2 ~=~ 4 ~-~ 1 ~=~ 3 \quad\Rightarrow\quad
\fbox{$e ~=~ \sqrt{3}$} ~. \nonumber \]
For triangle \(\triangle\,XYZ \), the Pythagorean Theorem says that
\[\nonumber 1^2 ~+~ 1^2 ~=~ z^2 \quad\Rightarrow\quad z^2 ~=~ 2 \quad\Rightarrow\quad
\fbox{$z ~=~ \sqrt{2}$} ~. \nonumber \]
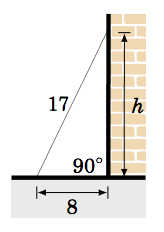
A 17 ft ladder leaning against a wall has its foot 8 ft from the base of the wall. At what height is the top of the ladder touching the wall?
Solution
Let \(h \) be the height at which the ladder touches the wall. We can assume that the ground makes a right angle with the wall, as in the picture on the right. Then we see that the ladder, ground, and wall form a right triangle with a hypotenuse of length 17 ft (the length of the ladder) and legs with lengths 8 ft and \(h \) ft. So by the Pythagorean Theorem, we have
\[\nonumber h^2 ~+~ 8^2 ~=~ 17^2 \quad\Rightarrow\quad h^2 ~=~ 289 ~-~ 64 ~=~ 225 \quad\Rightarrow\quad
\fbox{$h ~=~ 15 ~\text{ft}$} ~. \nonumber \]


