2.E: General Triangles (Exercises)

These are homework exercises to accompany Corral's "Elementary Trigonometry" Textmap. This is a text on elementary trigonometry, designed for students who have completed courses in high-school algebra and geometry. Though designed for college students, it could also be used in high schools. The traditional topics are covered, but a more geometrical approach is taken than usual. Also, some numerical methods (e.g. the secant method for solving trigonometric equations) are discussed.

2.1 Exercises

For Exercises 1-9, solve the triangle $△ ABC$.

2.1.1 $a = 10, A = 35^\circ , B = 25^\circ$

2.1.2 $b = 40, B = 75^\circ , c = 35$

2.1.3 $A = 40^\circ , B = 45^\circ , c = 15$

2.1.4 $a = 5, A = 42^\circ , b = 7$

2.1.5 $a = 40, A = 25^\circ , c = 30$

2.1.6 $a = 5, A = 47^\circ , b = 9$

2.1.7 $a = 12, A = 94^\circ , b = 15$

2.1.8 $a = 15, A = 94^\circ , b = 12$

2.1.9 $a = 22, A = 50^\circ , c = 27$

2.1.10 Draw a circle with a radius of 2 inches and inscribe a triangle inside the circle. Use a ruler and a protractor to measure the sides $a, b, c$ and the angles $A, B, C$ of the triangle. The Law of Sines says that the ratios $\frac{a}{ \sin A} , \frac{b}{ \sin B} , \frac{c}{ \sin C}$ are equal. Verify this for your triangle. What relation does that common ratio have to the diameter of your circle?

2.1.11 An observer on the ground measures an angle of inclination of $30^\circ$ to an approaching airplane, and 10 seconds later measures an angle of inclination of $55^\circ$. If the airplane is flying at a constant speed and at a steady altitude of 6000 ft in a straight line directly over the observer, find the speed of the airplane in miles per hour. (Note: 1 mile = 5280 ft)

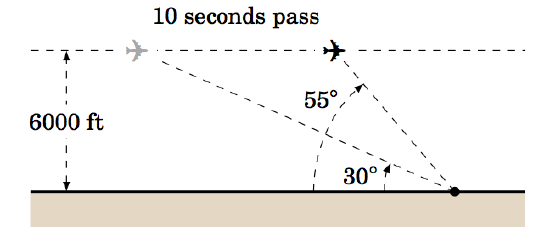
2.1.12 Prove the Law of Sines for right triangles. (Hint: One of the angles is known.)

2.1.13 For a triangle $△ ABC$, show that $\frac{a± b}{ c} = \frac{\sin A ± \sin B}{ \sin C}$.

2.1.14 For a triangle $△ ABC$, show that $\frac{a}{ c} = \frac{\sin (B +C)}{ \sin C}$.

2.1.15 One diagonal of a parallelogram is 17 cm long and makes angles of $36^\circ$ and $15^\circ$ with the sides. Find the lengths of the sides.

2.1.16 Explain why in Case 1 (one side and two angles) there is always exactly one solution.

---

2.2 Exercises

For Exercises 1-6, solve the triangle $\triangle\,ABC$.

2.2.1 $A = 60^\circ$, $b = 8$, $c = 12$

2.2.2 $A = 30^\circ$, $b = 4$, $c = 6$

2.2.3 $a = 7$, $B = 60^\circ$, $c = 9$

2.2.4 $a = 7$, $b = 3$, $c = 9$

2.2.5 $a = 6$, $b = 4$, $c = 1$

2.2.6 $a = 11$, $b = 13$, $c = 16$

2.2.7 The diagonals of a parallelogram intersect at a $42^\circ$ angle and have lengths of $12$ and $7$ cm. Find the lengths of the sides of the parallelogram. (Hint: The diagonals bisect each other.)

2.2.8 Two trains leave the same train station at the same time, moving along straight tracks that form a $35^\circ$ angle. If one train travels at an average speed of $100$ mi/hr and the other at an average speed of $90$ mi/hr, how far apart are the trains after half an hour?

2.2.9 Three circles with radii of $4$, $5$, and $6$ cm, respectively, are tangent to each other externally. Find the angles of the triangle whose vertexes are the centers of the circles.

2.2.10 Find the length $x$ of the diagonal of the quadrilateral in Figure 2.2.3 below.

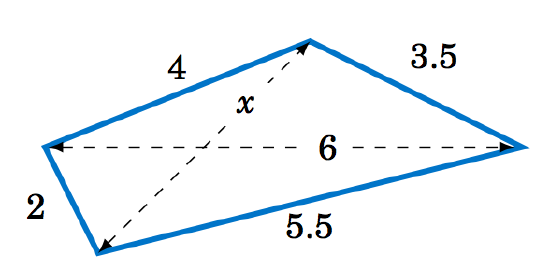
Figure 2.2.3 Exercise 10

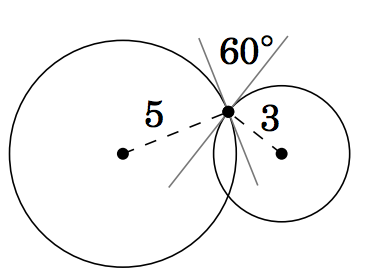
Figure 2.2.4 Exercise 11

2.2.11 Two circles of radii $5$ and $3$ cm, respectively, intersect at two points. At either point of intersection, the tangent lines to the circles form a $60^\circ$ angle, as in Figure 2.2.4 above. Find the distance between the centers of the circles.

2.2.12 Use the Law of Cosines to show that for any triangle $\triangle\,ABC$, $c^2 < a^2 + b^2$ if $C$ is acute, $c^2 > a^2 + b^2$ if $C$ is obtuse, and $c^2 = a^2 + b^2$ if $C$ is a right angle.

2.2.13 Show that for any triangle $\triangle\,ABC$,
$$\nonumber \frac{\cos\;A}{a} ~+~ \frac{\cos\;B}{b} ~+~ \frac{\cos\;C}{c} ~=~ \frac{a^2 + b^2 + c^2}{2abc}~.$$

2.2.14 Show that for any triangle $\triangle\,ABC$,
$$\nonumber \cos\;A ~+~ \cos\;B ~+~ \cos\;C ~=~ \frac{a^2 \;(b+c-a)~+~ b^2 \;(a+c-b)~+~ c^2 \;(a+b-c)}{2abc}~.$$
What do the terms in parentheses represent geometrically? Use your answer to explain why $\;\cos\;A ~+~ \cos\;B ~+~ \cos\;C ~>~0\,$ for any triangle, even if one of the cosines is negative.

2.2.15 Prove the Law of Cosines (i.e. Equations 2.9-2.11) for right triangles.

2.2.16 Recall from elementary geometry that a median of a triangle is a line segment from any vertex to the midpoint of the opposite side. Show that the sum of the squares of the three medians of a triangle is $\frac{3}{4}$ the sum of the squares of the sides.

2.2.17 The Dutch astronomer and mathematician Willebrord Snell (1580-1626) wrote the Law of Cosines as
$$\frac{2ab}{c^2 \;-\; (a - b)^2} ~=~ \frac{1}{1 \;-\; \cos\;C}$$
in his trigonometry text Doctrina triangulorum (published a year after his death). Show that this formula is equivalent to Equation 2.11 in our statement of the Law of Cosines.

2.2.18 Suppose that a satellite in space, an earth station, and the center of the earth all lie in the same plane. Let $r_e$ be the radius of the earth, let $r_s$ be the distance from the center of the earth to the satellite (called the orbital radius of the satellite), and let $d$ be the distance from the earth station to the satellite. Let $E$ be the angle of elevation from the earth station to the satellite, and let $\gamma$ and $\psi$ be the angles shown in Figure 2.25.

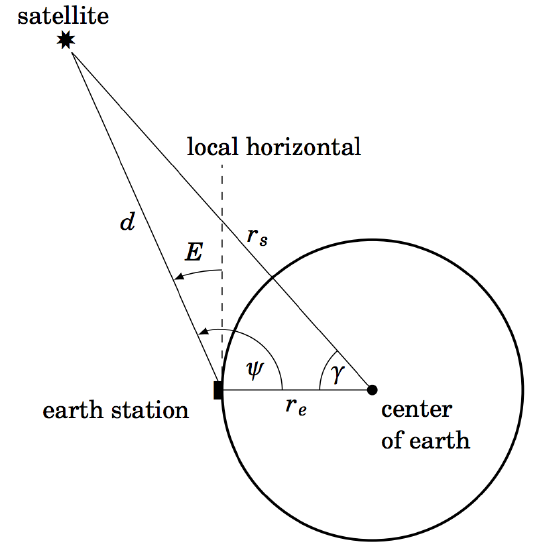
Figure 2.2.5

Use the Law of Cosines to show that
$$d ~=~ r_s \,\sqrt{1 \;+\; \left( \frac{r_e}{r_s} \right)^2 \;-\; 2\,\left( \frac{r_e}{r_s} \right) \,\cos\;\gamma} ~~,$$
and then use $E=\psi-90^\circ$ and the Law of Sines to show that
$$\cos\;E ~=~ \dfrac{\sin\;\gamma}{\sqrt{1 \;+\; \left( \dfrac{r_e}{r_s} \right)^2 \;-\; 2\,\left( \dfrac{r_e}{r_s} \right) \,\cos\;\gamma}} ~.$$
Note: This formula allows the angle of elevation $E$ to be calculated from the coordinates of the earth station and the subsatellite point (where the line from the satellite to the center of the earth crosses the surface of the earth).

---

2.3 Exercises

For Exercises 1-3, use the Law of Tangents to solve the triangle $\triangle\,ABC$.

2.3.1 $a = 12$, $b = 8$, $C = 60^\circ$

2.3.2 $A = 30^\circ$, $b = 4$, $c = 6$

2.3.3 $a = 7$, $B = 60^\circ$, $c = 9$

For Exercises 4-6, check if it is possible for a triangle to have the given parts.

2.3.4 $a=5$, $b=7$, $c=10$, $A=27.7^\circ$, $B=40.5^\circ$, $C=111.8^\circ$

2.3.5 $a=3$, $b=7$, $c=9$, $A=19.2^\circ$, $B=68.2^\circ$, $C=92.6^\circ$

2.3.6 $a=6$, $b=9$, $c=9$, $A=39^\circ$, $B=70.5^\circ$, $C=70.5^\circ$

2.3.7 Let $\triangle\,ABC$ be a right triangle with $C=90^\circ$. Show that $\;\tan\;\frac{1}{2}(A-B) =\frac{a-b}{a+b}\,$.

2.3.8 For any triangle $\triangle\,ABC$, show that $\;\tan\;\frac{1}{2}(A-B) = \frac{a-b}{a+b}\;\cot\;\frac{1}{2}C\,$.

2.3.9 For any triangle $\triangle\,ABC$, show that $\;\tan\;A = \dfrac{a\;\sin\;B}{c - a\;\cos\;B}\,$. (Hint: Draw the altitude from the vertex $C$ to $\overline{AB}$.) Notice that this formula provides another way of solving a triangle in Case 3 (two sides and the included angle).

2.3.10 For any triangle $\triangle\,ABC$, show that $\;c = b\;\cos\;A + a\;\cos\;B\,$. This is another check of a triangle.

2.3.11 If $\,b\;\cos\;A = a\;\cos\;B\,$, show that the triangle $\triangle\,ABC$ is isosceles.

2.3.12 Let $ABCD$ be a quadrilateral which completely contains its two diagonals. The quadrilateral has eight parts: four sides and four angles. What is the smallest number of parts that you would need to know to solve the quadrilateral? Explain your answer.

---

2.4 Exercises

For Exercises 1-6, find the area of the triangle $\triangle\,ABC$.

2.4.1 $A = 70^\circ$, $b = 4$, $c = 12$

2.4.2 $a = 10$, $B = 95^\circ$, $c = 35$

2.4.3 $A = 10^\circ$, $B = 48^\circ$, $C = 122^\circ$, $c = 11$

2.4.4 $A = 171^\circ$, $B = 1^\circ$, $C = 8^\circ$, $b = 2$

2.4.5 $a = 2$, $b = 3$, $c = 4$

2.4.6 $a = 5$, $b=6$, $c = 5$

2.4.7 Find the area of the quadrilateral in Figure 2.4.3 below.

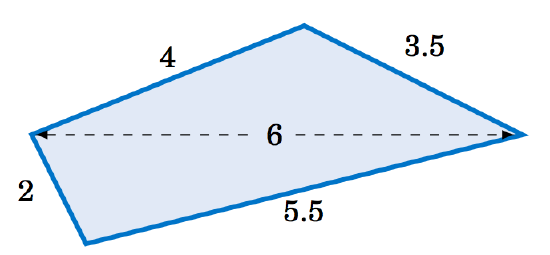
Figure 2.4.3 Exercise 7

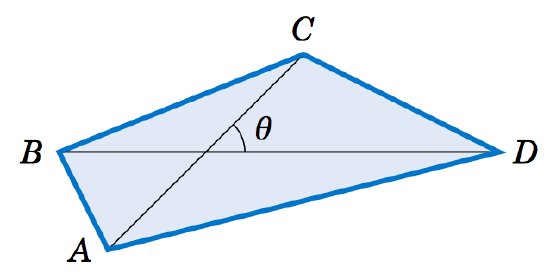
Figure 2.4.4 Exercise 8

2.4.8 Let $ABCD$ be a quadrilateral which completely contains its two diagonals, as in Figure 2.4.4 above. Show that the area $K$ of $ABCD$ is equal to half the product of its diagonals and the sine of the angle they form, i.e. $K = \frac{1}{2}\,AC\,\cdot\,BD\;\sin\;\theta\;$.

2.4.9 From Equation 2.26 derive the following formula for the area of a triangle $\triangle\,ABC$:
$$\text{Area} ~=~ K ~=~ \frac{a^2 \;\sin\;B \;\sin\;C}{2\;\sin\;(B+C)}$$
2.4.10 Show that the triangle area formula
$$\text{Area} ~=~ K ~=~ \tfrac{1}{4}\,\sqrt{(a + (b+c))\,(c - (a-b))\,(c + (a-b))\,(a + (b-c))}$$
is equivalent to Heron's formula. (Hint: In Heron's formula replace $s$ by $\frac{1}{2}(a+b+c)$.)
2.4.11 Show that the triangle area Equation 2.34 is equivalent to Heron's formula. (Hint: Factor the expression inside the square root.)

2.4.12 Find the angle $A$ in Example 2.16, then use Equation 2.23 to find the area. Did it work?

---

2.5 Exercises

For Exercises 1-6, find the radii $R$ and $r$ of the circumscribed and inscribed circles, respectively, of the triangle $\triangle\,ABC$.

2.5.1 $a = 2$, $b = 4$, $c = 5$

2.5.2 $a = 6$, $b = 8$, $c = 8$

2.5.3 $a = 5$, $b = 7$, $C = 40^\circ$

2.5.4 $A = 170^\circ$, $b = 100$, $c = 300$

2.5.5 $a = 10$, $b = 11$, $c = 20.5$

2.5.6 $a = 5$, $b = 12$, $c = 13$

For Exercises 7 and 8, draw the triangle $\triangle\,ABC$ and its circumscribed and inscribed circles accurately, using a ruler and compass (or computer software).

2.5.7 $a = 2$ in, $b = 4$ in, $c = 5$ in

2.5.8 $a = 5$ in, $b = 6$ in, $c = 7$ in

2.5.9 For any triangle $\triangle\,ABC$, let $s = \frac{1}{2}(a+b+c)$. Show that
$$\tan\;\tfrac{1}{2}A ~=~ \sqrt{\frac{(s-b)\,(s-c)}{s\,(s-a)}} ~~,~~~ \tan\;\tfrac{1}{2}B ~=~ \sqrt{\frac{(s-a)\,(s-c)}{s\,(s-b)}} ~~,~~~ \tan\;\tfrac{1}{2}C ~=~ \sqrt{\frac{(s-a)\,(s-b)}{s\,(s-c)}} ~~.$$
2.5.10 Show that for any triangle $\triangle\,ABC$, the radius $R$ of its circumscribed circle is
$$R ~=~ \frac{abc}{\sqrt{(a+b+c)\,(b+c-a)\,(a-b+c)\,(a+b-c)}} ~~.$$
2.5.11 Show that for any triangle $\triangle\,ABC$, the radius $R$ of its circumscribed circle and the radius $r$ of its inscribed circle satisfy the relation
$$rR ~=~ \frac{abc}{2\,(a+b+c)} ~~.$$
2.5.12 Let $\triangle\,ABC$ be an equilateral triangle whose sides are of length $a$.

(a) Find the exact value of the radius $R$ of the circumscribed circle of $\triangle\,ABC$.
(b) Find the exact value of the radius $r$ of the inscribed circle of $\triangle\,ABC$.
(c) How much larger is $R$ than $r$?
(d) Show that the circumscribed and inscribed circles of $\triangle\,ABC$ have the same center.

2.5.13 Let $\triangle\,ABC$ be a right triangle with $C=90^\circ$. Show that $\;\tan\;\tfrac{1}{2}A = \sqrt{\frac{c-b}{c+b}}~$.