These are homework exercises to accompany Corral's "Elementary Trigonometry" Textmap. This is a text on elementary trigonometry, designed for students who have completed courses in high-school algebra and geometry. Though designed for college students, it could also be used in high schools. The traditional topics are covered, but a more geometrical approach is taken than usual. Also, some numerical methods (e.g. the secant method for solving trigonometric equations) are discussed.
4.1 Exercise
For Exercises 1-5, convert the given angle to radians.
4.1.1 \(4^\circ\)
4.1.2 \(15^\circ\)
4.1.3 \(130^\circ\)
4.1.4 \(275^\circ\)
4.1.5 \(-108^\circ\)
For Exercises 6-10, convert the given angle to degrees.
4.1.6 \(4 \) rad
4.1.7 \(\dfrac{\pi}{5} \) rad
4.1.8 \(\dfrac{11\pi}{9} \) rad
4.1.9 \(\dfrac{29\pi}{30} \) rad
4.1.10 \(35 \) rad
4.1.11 Put your calculator in radian mode and take the cosine of \(0 \). Whatever the answer is, take its cosine. Then take the cosine of the new answer. Keep repeating this. On most calculators after about \(50\)-\(60 \) iterations you should start to see the same answer repeating. What is that number? Try starting with a number different from \(0 \). Do you get the same answer repeating after roughly the same number of iterations as before? Try the same procedure in degree mode, starting with \(0^\circ \). Does the same thing happen? If so, does it take fewer iterations for the answer to start repeating than in radian mode, or more?
4.2 Exercise
For Exercises 1-4, find the length of the arc cut off by the given central angle \(\theta \) in a circle of radius \(r \).
4.2.1 \(\theta=0.8 \) rad, \(r=12 \) cm
4.2.2 \(\theta=171^\circ \), \(r=8 \) m
4.2.3 \(\theta=\pi \) rad, \(r=11 \) in
4.2.4 A central angle in a circle of radius \(2 \) cm cuts off an arc of length \(4.6 \) cm. What is the measure of the angle in radians? What is the measure of the angle in degrees?
4.2.5 The centers of two belt pulleys, with radii of \(3 \) inches and \(6 \) inches, respectively, are \(13 \) inches apart. Find the total length \(L \) of the belt around the pulleys.
4.2.6 In Figure 4.2.5 one end of a \(4 \) ft iron rod is attached to the center of a pulley with radius \(0.5 \) ft. The other end is attached at a \(40^\circ \) angle to a wall, at a spot \(6 \) ft above the lower end of a steel wire supporting a box. The other end of the wire comes out of the wall straight across from the top of the pulley. Find the length \(L \) of the wire from the wall to the box.
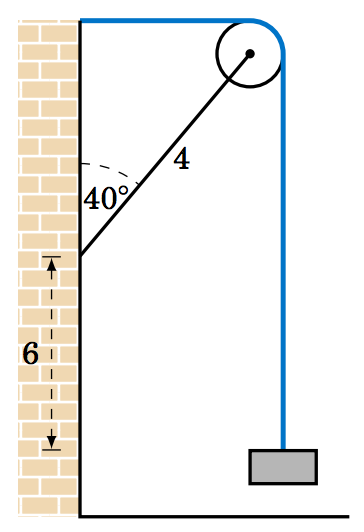
Figure 4.2.5 Exercise 6
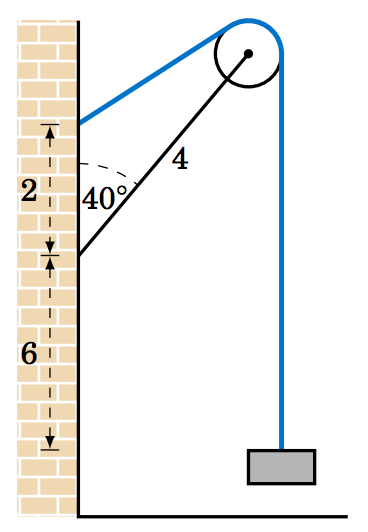
Figure 4.2.6 Exercise 7
4.2.7 Figure 4.2.6 shows the same setup as in Exercise 6 but now the wire comes out of the wall \(2 \) ft above where the rod is attached. Find the length \(L \) of the wire from the wall to the box.
4.2.8 Find the total length \(L \) of the figure eight shape in Figure 4.2.7.
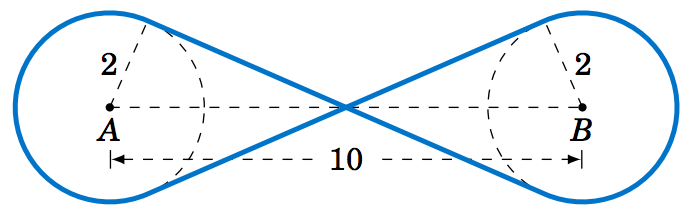
Figure 4.2.7
4.2.9 Repeat Exercise 8 but with the circle at \(A \) having a radius of \(3\) instead of \(2 \). (Hint: Draw a circle of radius \(5 \) centered at \(A \), then draw a tangent line to that circle from \(B \).)
4.2.10 Suppose that in Figure 4.2.7 the lines do not criss-cross but instead go straight across, as in a belt pulley system. Find the total length \(L \) of the resulting shape.
4.2.11 Find the lengths of the two arcs cut off by a chord of length \(3 \) in a circle of radius \(2 \).
4.2.12 Find the perimeter of a regular dodecagon (i.e. a \(12\)-sided polygon with sides of equal length) inscribed inside a circle of radius \(\frac{1}{2} \). Compare it to the circumference of the circle.
4.3 Exercise
For Exercises 1-3, find the area of the sector for the given angle \(\theta \) and radius \(r \).
4.3.1 \(\theta = 2.1 \) rad, \(r = 1.2 \) cm
4.3.2 \(\theta = \frac{3\pi}{7} \) rad, \(r = 3.5 \) ft
4.3.3 \(\theta = 78^\circ \), \(r = 6 \) m
4.3.4 The centers of two belt pulleys, with radii of \(3 \) cm and \(6 \) cm, respectively, are \(13 \) cm apart. Find the total area \(K \) enclosed by the belt.
4.3.5 In Exercise 4 suppose that both belt pulleys have the same radius of \(6 \) cm. Find the total area \(K \) enclosed by the belt.
4.3.6 Find the area enclosed by the figure eight in Exercise 8 from Section 4.2.
For Exercises 7-9, find the area of the sector for the given radius \(r \) and arc length \(s \).
4.3.7 \(r = 5 \) cm, \(s = 2 \) cm
4.3.8 \(r = a \), \(s = a\)
4.3.9 \(r = 1 \) cm, \(s = \pi \) cm
For Exercises 10-12, find the area of the segment formed by a chord of length \(a \) in a circle of radius \(r \).
4.3.10 \(a = 4 \) cm, \(r = 4 \) cm
4.3.11 \(a = 1 \) cm, \(r = 5 \) cm
4.3.12 \(a = 2 \) cm, \(r = 5 \) cm
4.3.13 Find the area of the shaded region in Figure 4.3.7.
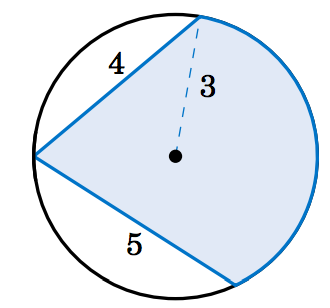
Figure 4.3.7 Exercise 13
4.3.14 Find the area of the shaded region in Figure 4.3.8. (Hint: Draw two central angles.)
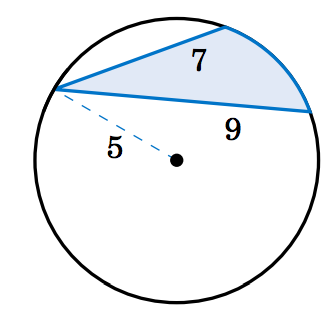
Figure 4.3.8 Exercise 14
4.3.15 Find the area of the shaded region in Figure 4.3.9.
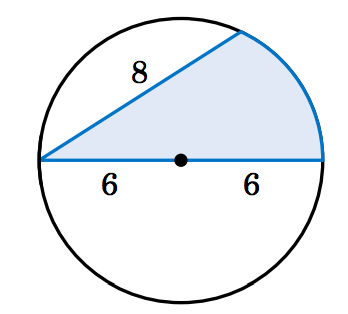
Figure 4.3.9 Exercise 15
4.3.16 The centers of two circles are \(4 \) cm apart, with one circle having a radius of \(3 \) cm and the other a radius of \(2 \) cm. Find the area of their intersection.
4.3.17 Three circles with radii of \(4 \) m, \(2 \) m, and \(1 \) m are externally tangent to each other. Find the area of the curved region between the circles, as in Figure 4.3.10. (Hint: Connect the centers of the circles.)
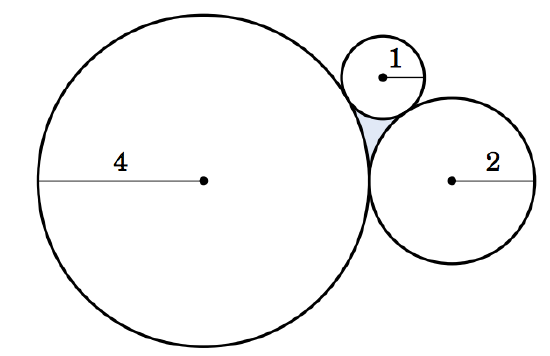
Figure 4.3.10 Exercise 17
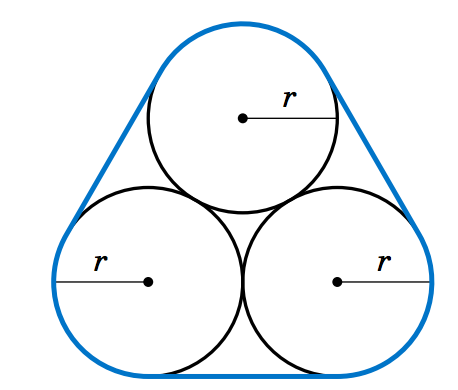
Figure 4.3.11 Exercise 18
4.3.18 Show that the total area enclosed by the loop around the three circles of radius \(r \) in Figure 4.3.11 is \(\;(\pi + 6 + \sqrt{3})\,r^2 \).
4.3.19 For a fixed central angle \(\theta \), how much does the area of its sector increase when the radius of the circle is doubled? How much does the length of its intercepted arc increase?
4.4 Exercise
For Exercises 1-6, assume that a particle moves along a circle of radius \(r \) for a period of time \(t \). Given either the arc length \(s \) or the central angle \(\theta \) swept out by the particle, find the linear and angular speed of the particle.
4.4.1 \(r=4 \) m, \(t=2 \) sec, \(\theta=3 \) rad
4.4.2 \(r=8 \) m, \(t=2 \) sec, \(\theta=3 \) rad
4.4.3 \(r=7 \) m, \(t=3.2 \) sec, \(\theta=172^\circ\)
4.4.4 \(r=1 \) m, \(t=1.6 \) sec, \(s=3 \) m
4.4.5 \(r=2 \) m, \(t=1.6 \) sec, \(s=6 \) m
4.4.6 \(r=1.5 \) ft, \(t=0.3 \) sec, \(s=4 \) in
4.4.7 An object moves at a constant linear speed of \(6 \) m/sec around a circle of radius \(3.2 \) m. How large of a central angle does it sweep out in \(1.8 \) seconds?
4.4.8 Two interlocking gears have outer radii of \(6 \) cm and \(9 \) cm, respectively. If the smaller gear rotates at \(40 \) rpm, how fast does the larger gear rotate?
4.4.9 Three interlocking gears have outer radii of \(2 \) cm, \(3 \) cm, and \(4 \) cm, respectively. If the largest gear rotates at \(16 \) rpm, how fast do the other gears rotate?
4.4.10 In Example 4.17, does equation 4.11 still hold if the radii \(r_1 \) and \(r_2 \) are replaced by the number of teeth \(N_1 \) and \(N_2 \), respectively, of the two gears as shown in Figure 4.4.2?
4.4.11 A \(78 \) rpm music record has a diameter of \(10 \) inches. What is the linear speed of a speck of dust on the outer edge of the record in inches per second?
4.4.12 The centripetal acceleration \(\alpha \) of an object moving along a circle of radius \(r \) with a linear speed \(\nu \) is defined as \(\;\alpha = \frac{\nu^2}{r} \). Show that \(\;\alpha = \omega^2 \,r \), where \(\omega \) is the angular speed.










