5.R: Trigonometric Functions (Review)
- Page ID
- 18195
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)5.1: Review Exercises
For the exercises 1-2, convert the angle measures to degrees.
1) \(\dfrac{π}{4}\)
- Answer
-
\(45°\)
2) \(−\dfrac{5π}{3}\)
For the exercises 3-6, convert the angle measures to radians.
3) \(-210°\)
- Answer
-
\(−\dfrac{7π}{6}\)
4) \(180°\)
5) Find the length of an arc in a circle of radius \(7\) meters subtended by the central angle of \(85°\).
- Answer
-
\(10.385\) meters
6) Find the area of the sector of a circle with diameter \(32\) feet and an angle of \(\dfrac{3π}{5}\) radians.
For the exercises 7-8, find the angle between \(0°\) and \(360°\) that is coterminal with the given angle.
7) \(420°\)
- Answer
-
\(60°\)
8) \(−80°\)
For the exercises 9-10, find the angle between \(0\) and \(2π\) in radians that is coterminal with the given angle.
9) \(− \dfrac{20π}{11}\)
- Answer
-
\(\dfrac{2π}{11}\)
10) \(\dfrac{14π}{5}\)
For the exercises 11-, draw the angle provided in standard position on the Cartesian plane.
11) \(-210°\)
- Answer
-
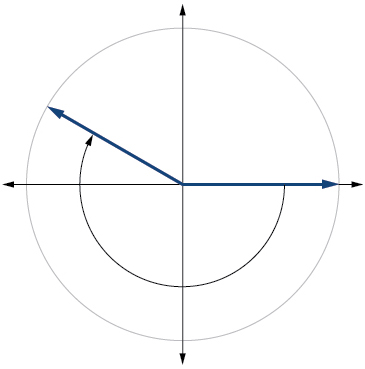
12) \(75°\)
13) \(\dfrac{5π}{4}\)
- Answer
-
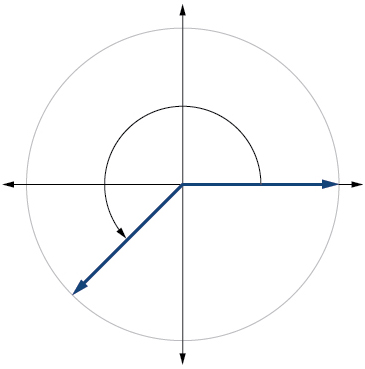
14) \(−\dfrac{π}{3}\)
15) Find the linear speed of a point on the equator of the earth if the earth has a radius of \(3,960\) miles and the earth rotates on its axis every \(24\) hours. Express answer in miles per hour.
- Answer
-
\(1036.73\) miles per hour
16) A car wheel with a diameter of \(18\) inches spins at the rate of \(10\) revolutions per second. What is the car's speed in miles per hour?
5.2: Review Exercises
1) Find the exact value of \( \sin \dfrac{π}{3}\).
- Answer
-
\(\dfrac{\sqrt{3}}{2}\)
2) Find the exact value of \( \cos \dfrac{π}{4}\).
3) Find the exact value of \( \cos π \).
- Answer
-
\(-1\)
4) State the reference angle for \(300°\).
5) State the reference angle for \( \dfrac{3π}{4}\).
- Answer
-
\( \dfrac{π}{4}\)
6) Compute cosine of \(330°\).
7) Compute sine of \(\dfrac{5π}{4}\).
- Answer
-
\(−\dfrac{\sqrt{2}}{2}\)
8) State the domain of the sine and cosine functions.
9) State the range of the sine and cosine functions.
- Answer
-
\([–1,1]\)
5.3: Review Exercises
For the exercises 1-4, find the exact value of the given expression.
1) \( \cos \dfrac{π}{6} \)
2) \( \tan \dfrac{π}{4} \)
- Answer
-
\(1\)
3) \( \csc \dfrac{π}{3}\)
4) \( \sec \dfrac{π}{4} \)
- Answer
-
\(\sqrt{2}\)
For the exercises 4-12, use reference angles to evaluate the given expression.
5) \( \sec \dfrac{11π}{3}\)
6) \( \sec 315°\)
- Answer
-
\( \sqrt{2}\)
7) If \( \sec (t)=−2.5\), what is the \( \sec (−t)\)?
8) If \( \tan (t)=−0.6 \), what is the \( \tan (−t)\)?
- Answer
-
\(0.6\)
9) If \( \tan (t)=\dfrac{1}{3}\), find \( \tan (t−π)\).
10) If \( \cos (t)= \dfrac{\sqrt{2}}{2}\), find \( \sin (t+2π)\).
- Answer
-
\(\dfrac{\sqrt{2}}{2}\) or \(−\dfrac{\sqrt{2}}{2}\)
11) Which trigonometric functions are even?
12) Which trigonometric functions are odd?
- Answer
-
sine, cosecant, tangent, cotangent
5.4: Review Exercises
For the exercises 1-5, use side lengths to evaluate.
1) \( \cos \dfrac{π}{4}\)
2) \( \cot \dfrac{π}{3}\)
- Answer
-
\(\dfrac{\sqrt{3}}{3}\)
3) \( \tan \dfrac{π}{6}\)
4) \( \cos (\dfrac{π}{2}) = \sin ( \_\_°)\)
- Answer
-
\(0\)
5) \( \csc (18°)= \sec (\_\_°)\)
For the exercises 6-7, use the given information to find the lengths of the other two sides of the right triangle.
6) \( \cos B= \dfrac{3}{5}, a=6\)
- Answer
-
\( b=8,c=10\)
7) \( \tan A = \dfrac{5}{9},b=6 \)
For the exercises 8-9, use Figure below to evaluate each trigonometric function.
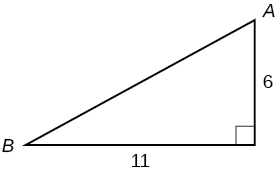
8) \( \sin A \)
- Answer
-
\( \dfrac{11\sqrt{157}}{157}\)
9) \( \tan B \)
For the exercises 10-11, solve for the unknown sides of the given triangle.
10)
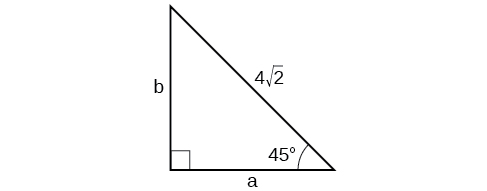
- Answer
-
\(a=4, b=4 \)
11)
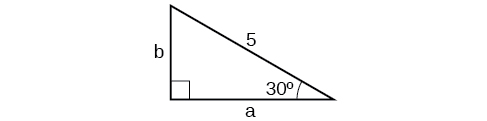
12) A \(15\)-ft ladder leans against a building so that the angle between the ground and the ladder is \(70°\). How high does the ladder reach up the side of the building?
- Answer
-
\(14.0954\) ft
13) The angle of elevation to the top of a building in Baltimore is found to be \(4\) degrees from the ground at a distance of \(1\) mile from the base of the building. Using this information, find the height of the building.
Practice Test
1) Convert \( \dfrac{5π}{6}\) radians to degrees.
- Answer
-
\(150°\)
2) Convert \(−620°\) to radians.
3) Find the length of a circular arc with a radius \(12\) centimeters subtended by the central angle of \(30°\).
- Answer
-
\(6.283\) centimeters
4) Find the area of the sector with radius of \(8\) feet and an angle of \(\dfrac{5π}{4}\) radians.
5) Find the angle between \(0°\) and \(360°\) that is coterminal with \(375°\).
- Answer
-
\(15°\)
6) Find the angle between \(0\) and \(2π\) in radians that is coterminal with \(−\dfrac{4π}{7}\).
7) Draw the angle \(315°\) in standard position on the Cartesian plane.
- Answer
-
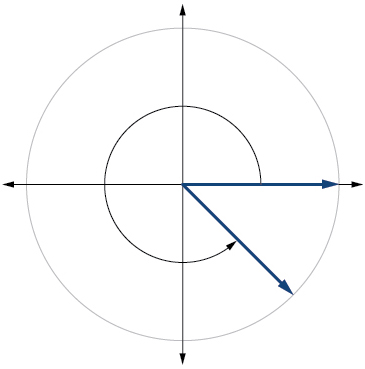
8) Draw the angle \(−\dfrac{π}{6}\) in standard position on the Cartesian plane.
9) A carnival has a Ferris wheel with a diameter of \(80\) feet. The time for the Ferris wheel to make one revolution is \(75\) seconds. What is the linear speed in feet per second of a point on the Ferris wheel? What is the angular speed in radians per second?
- Answer
-
\(3.351\) feet per second, \( \dfrac{2π}{75}\) radians per second
10) Find the exact value of \( \sin \dfrac{π}{6}\).
11) Compute sine of \(240°\).
- Answer
-
\(−\dfrac{\sqrt{3}}{2}\)
12) State the domain of the sine and cosine functions.
13) State the range of the sine and cosine functions.
- Answer
-
\([ –1,1 ]\)
14) Find the exact value of \( \cot \dfrac{π}{4}\).
15) Find the exact value of \( \tan \dfrac{π}{3}\).
- Answer
-
\( \sqrt{3}\)
16) Use reference angles to evaluate \( \csc \dfrac{7π}{4}\).
17) Use reference angles to evaluate \( \tan 210°\).
- Answer
-
\(\dfrac{\sqrt{3}}{3}\)
18) If \( \csc t=0.68\), what is the \( \csc (−t)\)?
19) If \( \cos t= \dfrac{\sqrt{3}}{2}\), find \( \cos (t−2π)\).
- Answer
-
\(\dfrac{\sqrt{3}}{2}\)
20) Which trigonometric functions are even?
21) Find the missing angle: \(\cos \left(\dfrac{\pi }{6} \right)= \sin (\;)\)
- Answer
-
\(\dfrac{π}{3}\)
22) Find the missing sides of the triangle \( ABC: \sin B= \dfrac{3}{4},c=12\)
23) Find the missing sides of the triangle.
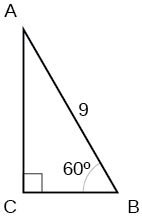
- Answer
-
\(a=\dfrac{9}{2},b=\dfrac{9\sqrt{3}}{2}\)
24) The angle of elevation to the top of a building in Chicago is found to be \(9\) degrees from the ground at a distance of \(2000\) feet from the base of the building. Using this information, find the height of the building.


