1.1: Sets of Real Numbers and the Cartesian Coordinate Plane
( \newcommand{\kernel}{\mathrm{null}\,}\)
Sets of Numbers
While the authors would like nothing more than to delve quickly and deeply into the sheer excitement that is Precalculus, experience has taught us that a brief refresher on some basic notions is welcome, if not completely necessary, at this stage. To that end, we present a brief summary of 'set theory' and some of the associated vocabulary and notations we use in the text. Like all good Math books, we begin with a definition.
Definition 1.1: Set
A set is a well-defined collection of objects which are called the 'elements' of the set. Here, 'well-defined' means that it is possible to determine if something belongs to the collection or not, without prejudice.
For example, the collection of letters that make up the word "smolko'' is well-defined and is a set, but the collection of the worst math teachers in the world is not well-defined, and so is not a set (for a more thought-provoking example, consider the collection of all things that do not contain themselves - this leads to the famous Russell's Paradox). In general, there are three ways to describe sets. They are
Ways to Describe Sets
- The Verbal Method: Use a sentence to define a set.
- The Roster Method: Begin with a left brace '
- The Set-Builder Method: A combination of the verbal and roster methods using a "dummy variable'' such as
For example, let
The way to read this is: 'The set of elements
or
Clearly
Sets of Numbers
- The Empty Set:
- The Natural Numbers:
- The Whole Numbers:
- The Integers:
- The Rational Numbers:
- The Real Numbers:
- The Irrational Numbers:
- The Complex Numbers:
It is important to note that every natural number is a whole number, which, in turn, is an integer. Each integer is a rational number (take

Figure
For the most part, this textbook focuses on sets whose elements come from the real numbers
Interval Notation
Let
| Set of Real Numbers | Interval Notation | Region on the Real Number Line |
|---|---|---|
We will often have occasion to combine sets. There are two basic ways to combine sets:
Definition 1.2: Intersection and Union
Suppose
- The intersection of
- The union of
Said differently, the intersection of two sets is the overlap of the two sets -- the elements which the sets have in common. The union of two sets consists of the totality of the elements in each of the sets, collected together (the reader is encouraged to research Venn Diagrams for a nice geometric interpretation of these concepts). For example, if
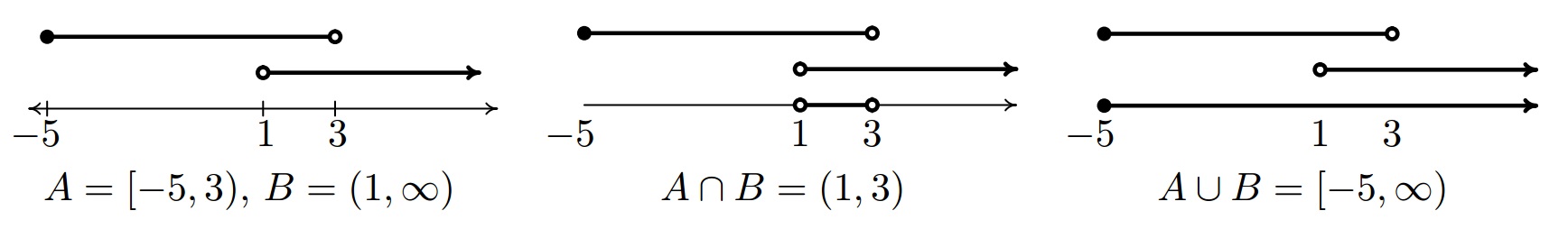
While both intersection and union are important, we have more occasion to use union in this text than intersection, simply because most of the sets of real numbers we will be working with are either intervals or are unions of intervals, as the following example illustrates.
Example
Express the following sets of numbers using interval notation.
Solution
- The best way to proceed here is to graph the set of numbers on the number line and glean the answer from it. The inequality
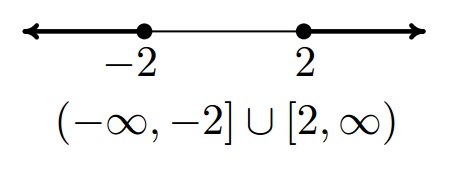
- For the set
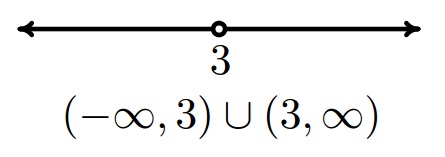
- For the set
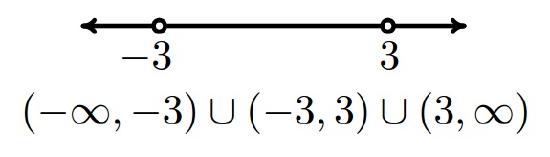
- Graphing the set
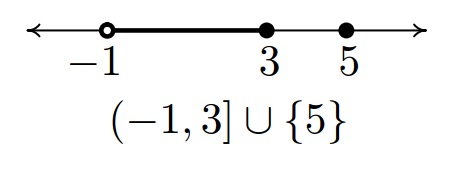
The Cartesian Coordinate Plane
In order to visualize the pure excitement that is Precalculus, we need to unite Algebra and Geometry. Simply put, we must find a way to draw algebraic things. Let's start with possibly the greatest mathematical achievement of all time: the Cartesian Coordinate Plane. Imagine two real number lines crossing at a right angle at
The horizontal number line is usually called the
Having two number lines allows us to locate the positions of points off of the number lines as well as points on the lines themselves.
For example, consider the point
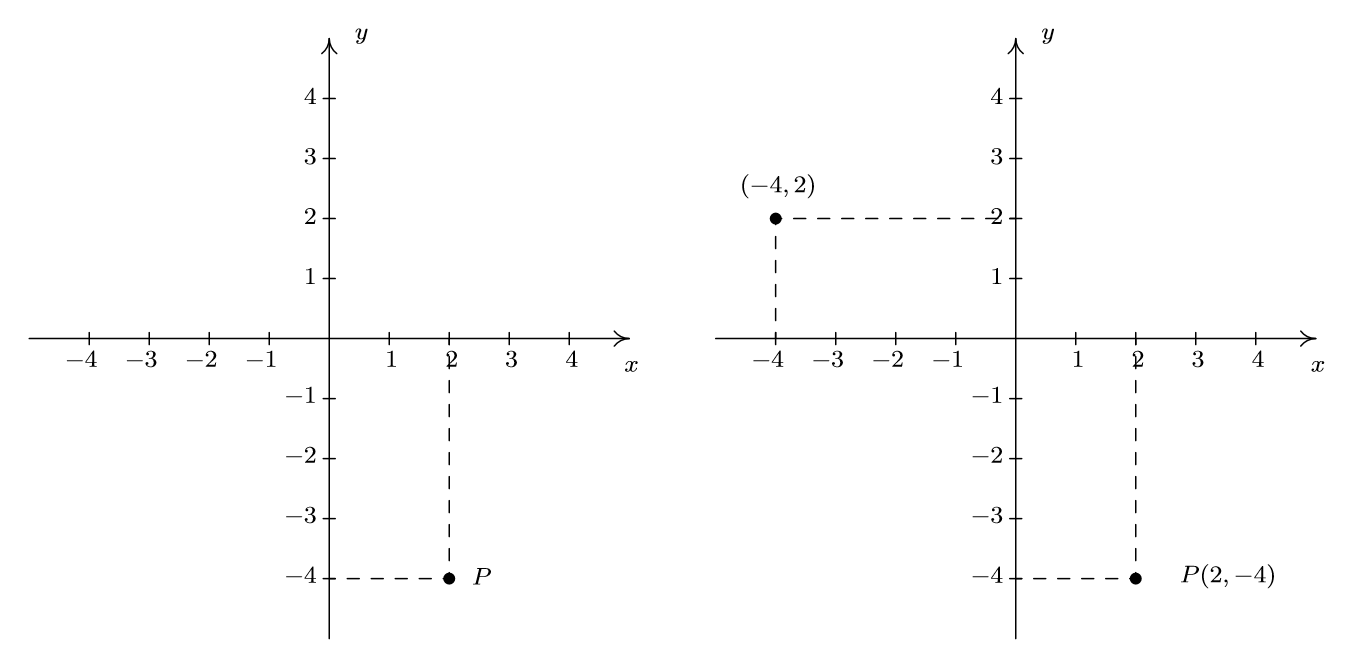
When we speak of the Cartesian Coordinate Plane, we mean the set of all possible ordered pairs
Important Facts about the Cartesian Coordinate Plane
- The origin is the point
Example
Plot the following points:
By the way, the letter
Solution
To plot these points, we start at the origin and move to the right if the
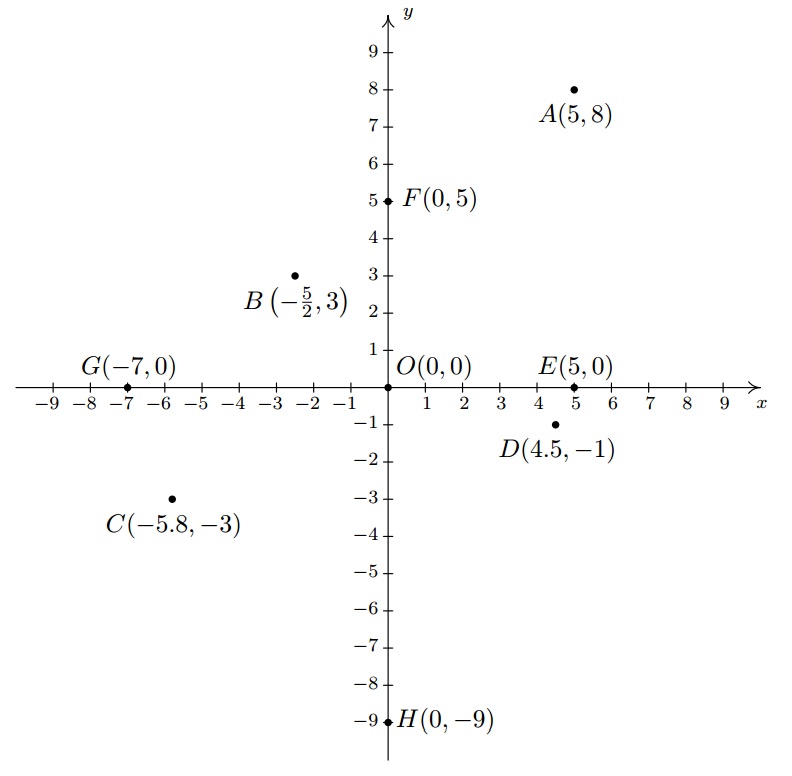
The axes divide the plane into four regions called quadrants. They are labeled with Roman numerals and proceed counterclockwise around the plane:
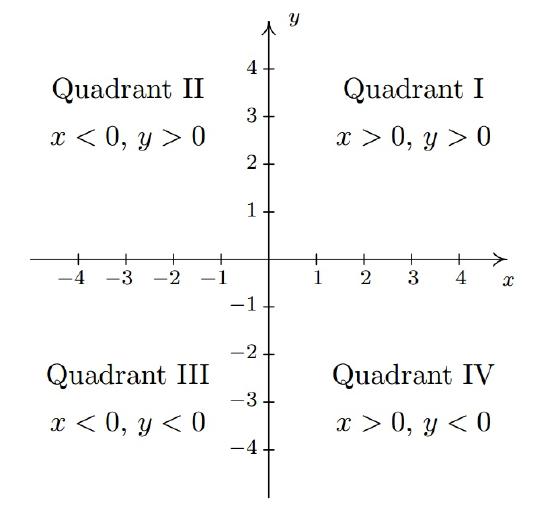
For example,
One of the most important concepts in all of Mathematics is symmetry. There are many types of symmetry in Mathematics, but three of them can be discussed easily using Cartesian Coordinates.
Definition 1.3: Symmetries
Two points
- symmetric about the
- symmetric about the
- symmetric about the origin if
Schematically,

In the above figure,
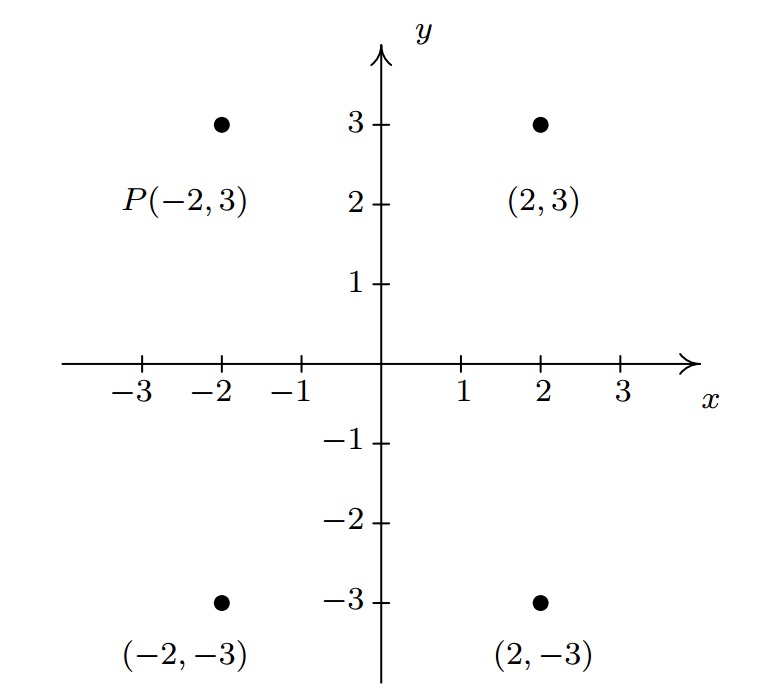
Example
Let
- origin
Check your answer by plotting the points.
Solution
The figure after Definition
- To find the point symmetric about the
- To find the point symmetric about the
- To find the point symmetric about the origin, we replace the
One way to visualize the processes in the previous example is with the concept of a reflection. If we start with our point
Reflections
To reflect a point
- origin, replace
Distance in the Plane
Another important concept in Geometry is the notion of length. If we are going to unite Algebra and Geometry using the Cartesian Plane, then we need to develop an algebraic understanding of what distance in the plane means. Suppose we have two points,
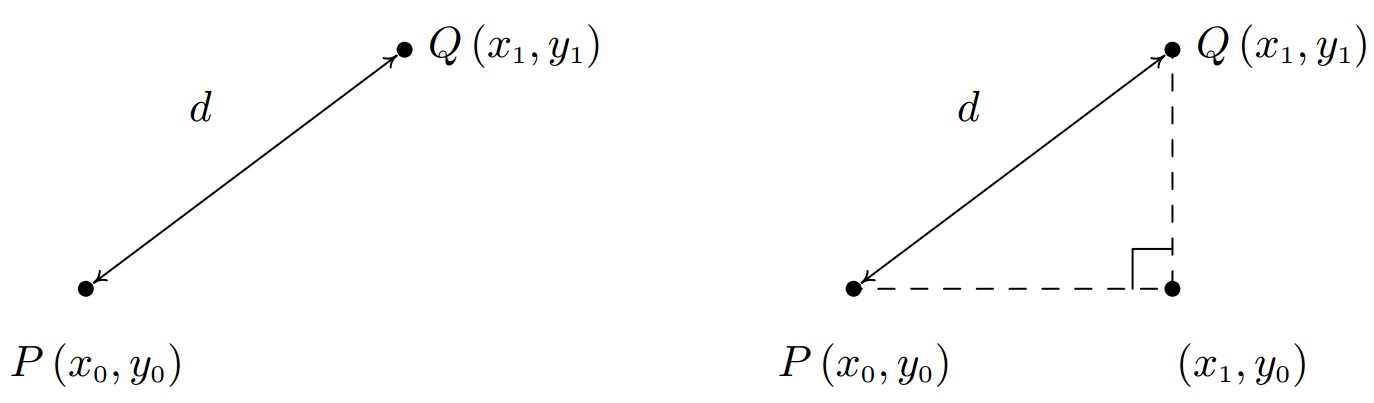
With a little more imagination, we can envision a right triangle whose hypotenuse has length
(Do you remember why we can replace the absolute value notation with parentheses?) By extracting the square root of both sides of the second equation and using the fact that distance is never negative, we get
equation 1.1: The Distance Formula
The distance
It is not always the case that the points
Example
Find and simplify the distance between
Solution
\setlength{\extrarowheight}{3pt}
So the distance is
Example
Find all of the points with
Solution
We shall soon see that the points we wish to find are on the line
We require that the distance from
We obtain two answers:
Related to finding the distance between two points is the problem of finding the midpoint of the line segment connecting two points. Given two points,
If we think of reaching
The Midpoint Formula
The midpoint
If we let
Example
Find the midpoint of the line segment connecting
Solution
The midpoint is
We close with a more abstract application of the Midpoint Formula. We will revisit the following example in Exercise
Example
If
Solution
To prove the claim, we use Equation
Since the

