4.3: Logarithmic Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
A population of 50 flies is expected to double every week, leading to a function of the form f(x)=50(2)x, where x represents the number of weeks that have passed. When will this population reach 500? Trying to solve this problem leads to:
500=50(2)x Dividing both sides by 50 to isolate the exponential
10=2x
While we have set up exponential models and used them to make predictions, you may have noticed that solving exponential equations has not yet been mentioned. The reason is simple: none of the algebraic tools discussed so far are sufficient to solve exponential equations. Consider the equation 2x=10 above. We know that 23=8 and 24=16, so it is clear that x must be some value between 3 and 4 since g(x)=2x is increasing. We could use technology to create a table of values or graph to better estimate the solution.
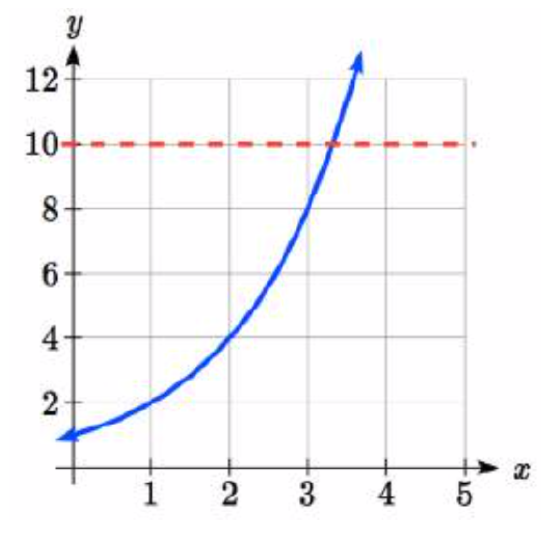
From the graph, we could better estimate the solution to be around 3.3. This result is still fairly unsatisfactory, and since the exponential function is one-to-one, it would be great to have an inverse function. None of the functions we have already discussed would serve as an inverse function and so we must introduce a new function, named log as the inverse of an exponential function. Since exponential functions have different bases, we will define corresponding logarithms of different bases as well.
Definition: logarithm
The logarithm (base b) function, written logb(x), is the inverse of the exponential function (base b), bx.
Since the logarithm and exponential are inverses, it follows that:
properties of logs: inverse properties
logb(bx)=x
blogbx=x
Recall from the definition of an inverse function that if f(a)=c, then f−1(c)=a. Applying this to the exponential and logarithmic functions, we can convert between a logarithmic equation and its equivalent exponential.
logarithm equivalent to an exponential
The statement ba=c is equivalent to the statement logb(c)=a.
Alternatively, we could show this by starting with the exponential functionc=ba, then taking the log base b of both sides, giving logb(c)=logbba. Using the inverse property of logs, we see that logb(c)=a.
Since log is a function, it is most correctly written as logb(c), using parentheses to denote function evaluation, just as we would with f(c). However, when the input is a single variable or number, it is common to see the parentheses dropped and the expression written as logbc.
Example 4.3.1
Write these exponential equations as logarithmic equations:
- 23=8
- 52=25
- 10−4=110000
Solution
a) 23=8 is equivalent to log2(8)=3
b) 52=25 is equivalent to log5(25)=2
c) 10−4=110000 is equivalent to log10(110000)=−4
Example 4.3.2
Write these logarithmic equations as exponential equations:
a) log6(√6)=12 b) log3(9)=2
Solution
a) log6(√6)=12 is equivalent to 61/2=√6
b) log3(9)=2 is equivalent to 32=9
Exercise 4.3.1
Write the exponential equation 42=16 as a logarithmic equation.
- Answer
-
log4(16)=2=log442=2log44
By establishing the relationship between exponential and logarithmic functions, we can now solve basic logarithmic and exponential equations by rewriting.
Example 4.3.3
Solve log4(x)=2 for x.
Solution
By rewriting this expression as an exponential, 42=x, so x=16.
Example 4.3.4
Solve 2x=10 for x.
Solution
By rewriting this expression as a logarithm, we get x=log2(10).
While this does define a solution, and an exact solution at that, you may find it somewhat unsatisfying since it is difficult to compare this expression to the decimal estimate we made earlier. Also, giving an exact expression for a solution is not always useful – often we really need a decimal approximation to the solution. Luckily, this is a task calculators and computers are quite adept at. Unluckily for us, most calculators and computers will only evaluate logarithms of two bases. Happily, this ends up not being a problem, as we’ll see briefly.
Definition: common and natural logarithms
The common log is the logarithm with base 10, and is typically written log(x).
The natural log is the logarithm with base e, and is typically written ln(x).
Example 4.3.5
Evaluate log(1000) using the definition of the common log.
| number | number as exponential | log(number) |
|---|---|---|
| 1000 | 103 | 3 |
| 100 | 102 | 2 |
| 10 | 101 | 1 |
| 1 | 100 | 0 |
| 0.1 | 10−1 | -1 |
| 0.01 | 10−2 | -2 |
| 0.001 | 10−3 | -3 |
Solution
To evaluate log(1000), we can let x=log(1000), then rewrite into exponential form using the common log base of 10:
10x=1000.
From this, we might recognize that 1000 is the cube of 10, so x = 3.
We also can use the inverse property of logs to write log10(103)=3.
Exercise 4.3.2
Evaluate log(1000000).
- Answer
-
log(1000000)=log(106)=6
Example 4.3.6
Evaluate ln(√e).
Solution
We can rewrite ln(√e) as ln(e1/2). Since ln is a log base e, we can use the inverse property for logs: ln(e1/2)=loge(e1/2)=12.
Example 4.3.7
Evaluate log(500) using your calculator or computer.
Solution
Using a computer, we can evaluate log(500)≈2.69897
To utilize the common or natural logarithm functions to evaluate expressions like log2(10), we need to establish some additional properties.
properties of logs: exponent property
logb(Ar)=rlogb(A)
To show why this is true, we offer a proof:
Since the logarithmic and exponential functions are inverses, blogbA=A.
Raising both sides to the r power, we get Ar=(blogbA)r.
Utilizing the exponential rule that states(xp)q=xpq, Ar=(blogbA)r=brlogbA
Taking the log of both sides, logb(Ar)=logb(brlogbA)
Utilizing the inverse property on the right side yields the result: logb(Ar)=rlogbA
Example 4.3.8
Rewrite log3(25) using the exponent property for logs.
Solution
Since 25 = 52,
log3(25)=log3(52)=2log3(5)
Example 4.3.9
Rewrite 4ln(x)using the exponent property for logs.
Solution
Using the property in reverse, 4ln(x)=ln(x4).
Exercise 4.3.3
Rewrite using the exponent property for logs: ln(1x2).
- Answer
-
3.ln(1x2)=ln(x−2)=−2ln(x)
The exponent property allows us to find a method for changing the base of a logarithmic expression.
properties of logs: change of base
logb(A)=logc(A)logc(b)
Proof
Let logb(A)=x.
Rewriting as an exponential gives bx=A.
Taking the log base c of both sides of this equation gives
logcbx=logcA
Now utilizing the exponent property for logs on the left side,
xlogcb=logcA
Dividing, we obtain x=logcAlogcb. Replacing our original expression for x,
logbA=logcAlogcb
With this change of base formula, we can finally find a good decimal approximation to our question from the beginning of the section.
Example 4.3.10
Evaluate log2(10) using the change of base formula.
Solution
According to the change of base formula, we can rewrite the log base 2 as a logarithm of any other base. Since our calculators can evaluate the natural log, we might choose to use the natural logarithm, which is the log base e:
log210=loge10loge2=ln10ln2
Using our calculators to evaluate this,
ln10ln2≈2.302590.69315≈3.3219
This finally allows us to answer our original question – the population of flies we discussed at the beginning of the section will take 3.32 weeks to grow to 500.
Example 4.3.11
Evaluate log5(100) using the change of base formula.
Solution
We can rewrite this expression using any other base. If our calculators are able to evaluate the common logarithm, we could rewrite using the common log, base 10.
log5(100)=log10100log105≈20.69897=2.861
While we can solve the basic exponential equation 2x=10 by rewriting in logarithmic form and then using the change of base formula to evaluate the logarithm, the proof of the change of base formula illuminates an alternative approach to solving exponential equations.
Solving Exponential Equations
- Isolate the exponential expressions when possible
- Take the logarithm of both sides
- Utilize the exponent property for logarithms to pull the variable out of the exponent
- Use algebra to solve for the variable.
Example 4.3.12
Solve 2x=10 for x.
Solution
Using this alternative approach, rather than rewrite this exponential into logarithmic form, we will take the logarithm of both sides of the equation. Since we often wish to evaluate the result to a decimal answer, we will usually utilize either the common log or natural log. For this example, we’ll use the natural log:
ln(2x)=ln(10) Utilizing the exponent property for logs,
xln(2)=ln(10) Now dividing by ln(2),
x=ln(10)ln(2)≈3.3219
Notice that this result matches the result we found using the change of base formula.
Example 4.3.13
In the first section, we predicted the population (in billions) of India t years after 2008 by using the function f(t)=1.14(1+0.0134)t. If the population continues following this trend, when will the population reach 2 billion?
Solution
We need to solve for time t so that f(t)=2.
2=1.14(1.0134)t Divide by 1.14 to isolate the exponential expression
21.14=1.0134t Take the logarithm of both sides of the equation
ln(21.14)=ln(1.0134t) Apply the exponent property on the right side
ln(21.14)=tln(1.0134) Divide both sides by ln(1.0134)
t=ln(21.14)ln(1.0134)≈42.23 years
If this growth rate continues, the model predicts the population of India will reach 2 billion about 42 years after 2008, or approximately in the year 2050.
Exercise 4.3.4
Solve 5(0.93)x=10.
- Answer
-
5(0.93)x=10(0.93)x=2ln(0.93x)=ln(2)xln(0.93)=ln(2)ln(2)ln(0.93)≈−9.5513
Example 4.3.14
Solve 5(1.07)3t=2
Solution
To start, we want to isolate the exponential part of the expression, the (1.07)3t, so it is alone on one side of the equation. Then we can use the log to solve the equation. We can use any base log; this time we’ll use the common log.
5(1.07)3t=2 Divide both sides by 5 to isolate the exponential
(1.07)3t=25 Take the log of both sides.
log((1.07)3t)=log(25) Use the exponent property for logs
3tlog(1.07)=log(25) Divide by 3log(1.07) on both sides
3tlog(1.07)3log(1.07)=log(25)3log(1.07) Simplify and evaluate
t=log(25)3log(1.07)≈−4.5143
Note that when entering that expression on your calculator, be sure to put parentheses around the whole denominator to ensure the proper order of operations:
log(2/5)/(3*log(1.07))
In addition to solving exponential equations, logarithmic expressions are common in many physical situations.
Example 4.3.15
In chemistry, pH is a measure of the acidity or basicity of a liquid. The pH is related to the concentration of hydrogen ions, [H+], measured in moles per liter, by the equation
pH=−log([H+])
If a liquid has concentration of 0.0001 moles per liber, determine the pH.
Determine the hydrogen ion concentration of a liquid with pH of 7.
Solution
To answer the first question, we evaluate the expression −log(0.0001). While we could use our calculators for this, we do not really need them here, since we can use the inverse property of logs:
−log(0.0001)=−log(10−4)=−(−4)=4
To answer the second question, we need to solve the equation 7=−log([H+]). Begin by isolating the logarithm on one side of the equation by multiplying both sides by -1:
−7=log([H+]). Rewriting into exponential form yields the answer:
[H+]=10−7=0.0000001 moles per liter
Logarithms also provide us a mechanism for finding continuous growth models for exponential growth given two data points.
Example 4.3.16
A population grows from 100 to 130 in 2 weeks. Find the continuous growth rate.
Solution
Measuring t in weeks, we are looking for an equation P(t)=aert so that P(0) = 100 and P(2) = 130. Using the first pair of values,
100=aer⋅0, so a = 100.
Using the second pair of values,
130=100er⋅2 Divide by 100
130100=er2 Take the natural log of both sides
ln(1.3)=ln(er2) Use the inverse property of logs
ln(1.3)=2rr=ln(1.3)2≈0.1312
This population is growing at a continuous rate of 13.12% per week.
In general, we can relate the standard form of an exponential with the continuous growth form by noting (using k to represent the continuous growth rate to avoid the confusion of using r in two different ways in the same formula):
a(1+r)x=aekx (1+r)x=ekx 1+r=ek
converting between periodic to continuous growth rate
In the equation f(x)=a(1+r)x, r is the periodic growth rate, the percent growth each time period (weekly growth, annual growth, etc.).
In the equation f(x)=aekx, k is the continuous growth rate.
You can convert between these using: 1+r=ek.
Remember that the continuous growth rate k represents the nominal growth rate before accounting for the effects of continuous compounding, while r represents the actual percent increase in one time unit (one week, one year, etc.).
Example 4.3.17
A company’s sales can be modeled by the function S(t)=5000e0.12t, with t measured in years. Find the annual growth rate.
Solution
Noting that 1+r=ek, then r=e0.12−1=0.1275, so the annual growth rate is 12.75%. The sales function could also be written in the form S(t)=5000(1+0.1275)t.
Important Topics of this Section
- The Logarithmic function as the inverse of the exponential function
- Writing logarithmic & exponential expressions
- Properties of logs
- Inverse properties
- Exponential properties
- Change of base
- Common log
- Natural log
- Solving exponential equations
- Converting between periodic and continuous growth rate.


