5.1E: Circles (Exercises)
- Page ID
- 13912
Section 5.1 Exercise
1. Find the distance between the points (5,3) and (-1,-5).
2. Find the distance between the points (3,3) and (-3,-2).
3. Write an equation of the circle centered at (8 , -10) with radius 8.
4. Write an equation of the circle centered at (-9, 9) with radius 16.
5. Write an equation of the circle centered at (7, -2) that passes through (-10, 0).
6. Write an equation of the circle centered at (3, -7) that passes through (15, 13).
7. Write an equation for a circle where the points (2, 6) and (8, 10) lie along a diameter.
8. Write an equation for a circle where the points (-3, 3) and (5, 7) lie along a diameter.
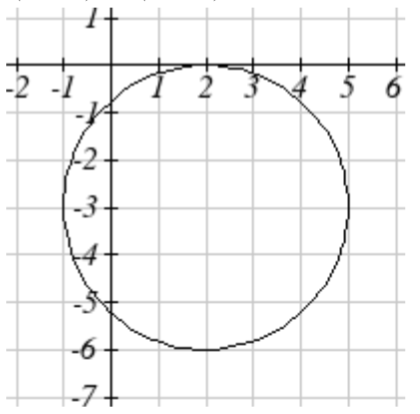
9. Sketch a graph of \(\left(x-2\right)^{2} + \left(y+3\right)^{2} = 9\).
10. Sketch a graph of \(\left(x+1\right)^{2} + \left(y-2\right)^{2} = 16\).
11. Find the \(y\) intercept(s) of the circle with center (2, 3) with radius 3.
12. Find the \(x\) intercept(s) of the circle with center (2, 3) with radius 4.
13. At what point in the first quadrant does the line with equation \(y = 2x + 5\) intersect a circle with radius 3 and center (0, 5)?
14. At what point in the first quadrant does the line with equation \(y = x + 2\) intersect the circle with radius 6 and center (0, 2)?
15. At what point in the second quadrant does the line with equation \(y = 2x + 5\) intersect a circle with radius 3 and center (-2, 0)?
16. At what point in the first quadrant does the line with equation \(y = x + 2\) intersect the circle with radius 6 and center (-1,0)?
17. A small radio transmitter broadcasts in a 53 mile radius. If you drive along a straight line from a city 70 miles north of the transmitter to a second city 74 miles east of the transmitter, during how much of the drive will you pick up a signal from the transmitter?
18. A small radio transmitter broadcasts in a 44 mile radius. If you drive along a straight line from a city 56 miles south of the transmitter to a second city 53 miles west of the transmitter, during how much of the drive will you pick up a signal from the transmitter?
19. 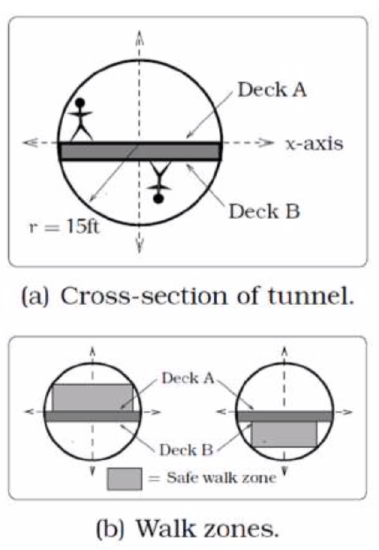 A tunnel connecting two portions of a space station has a circular cross-section of radius 15 feet. Two walkway decks are constructed in the tunnel. Deck A is along a horizontal diameter and another parallel Deck B is 2 feet below Deck A. Because the space station is in a weightless environment, you can walk vertically upright along Deck A, or vertically upside down along Deck B. You have been assigned to paint “safety stripes” on each deck level, so that a 6 foot person can safely walk upright along either deck. Determine the width of the “safe walk zone” on each deck. [UW]
A tunnel connecting two portions of a space station has a circular cross-section of radius 15 feet. Two walkway decks are constructed in the tunnel. Deck A is along a horizontal diameter and another parallel Deck B is 2 feet below Deck A. Because the space station is in a weightless environment, you can walk vertically upright along Deck A, or vertically upside down along Deck B. You have been assigned to paint “safety stripes” on each deck level, so that a 6 foot person can safely walk upright along either deck. Determine the width of the “safe walk zone” on each deck. [UW]
20. 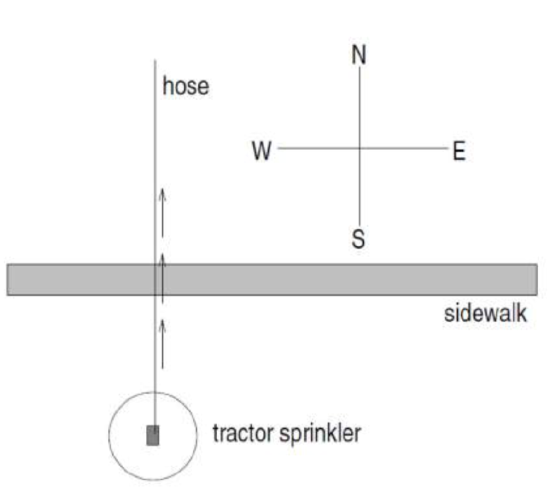 A crawling tractor sprinkler is located as pictured here, 100 feet south of a sidewalk. Once the water is turned on, the sprinkler waters a circular disc of radius 20 feet and moves north along the hose at the rate of 1/2 inch/second. The hose is perpendicular to the 10 ft. wide sidewalk. Assume there is grass on both sides of the sidewalk. [UW]
A crawling tractor sprinkler is located as pictured here, 100 feet south of a sidewalk. Once the water is turned on, the sprinkler waters a circular disc of radius 20 feet and moves north along the hose at the rate of 1/2 inch/second. The hose is perpendicular to the 10 ft. wide sidewalk. Assume there is grass on both sides of the sidewalk. [UW]
a. Impose a coordinate system. Describe the initial coordinates of the sprinkler and find equations of the lines forming and find equations of the lines forming the north and south boundaries of the sidewalk.
b. When will the water first strike the sidewalk?
c. When will the water from the sprinkler fall completely north of the sidewalk?
d. Find the total amount of time water from the sprinkler falls on the sidewalk.
e. Sketch a picture of the situation after 33 minutes. Draw an accurate picture of the watered portion of the sidewalk.
f. Find the area of grass watered after one hour.
21. 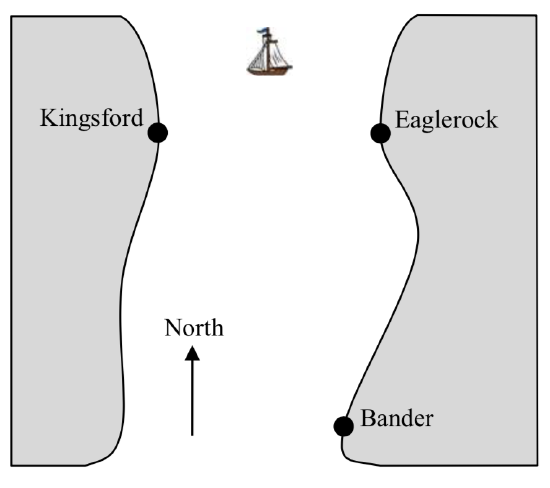 Erik’s disabled sailboat is floating anchored 3 miles East and 2 miles north of Kingsford. A ferry leaves Kingsford heading toward Eaglerock at 12 mph. Eaglerock is 6 miles due east of Kingsford. After 20 minutes the ferry turns, heading due south. Bander is 8 miles south and 1 mile west of Eaglerock. Impose coordinates with Bander as the origin. [UW]
Erik’s disabled sailboat is floating anchored 3 miles East and 2 miles north of Kingsford. A ferry leaves Kingsford heading toward Eaglerock at 12 mph. Eaglerock is 6 miles due east of Kingsford. After 20 minutes the ferry turns, heading due south. Bander is 8 miles south and 1 mile west of Eaglerock. Impose coordinates with Bander as the origin. [UW]
a. Find equations for the lines along which the ferry is moving and draw in these lines.
b. The sailboat has a radar scope that will detect any object within 3 miles of the sailboat. Looking down from above, as in the picture, the radar region looks like a circular disk. The boundary is the “edge” or circle around this disk, the interior is everything inside of the circle, and the exterior is everything outside of the circle. Give the mathematical description (an equation or inequality) of the boundary, interior and exterior of the radar zone. Sketch an accurate picture of the radar zone by determining where the line connecting Kingsford and Eaglerock would cross the radar zone.
c. When does the ferry enter the radar zone?
d. Where and when does the ferry exit the radar zone?
e. How long does the ferry spend inside the radar zone?
22. 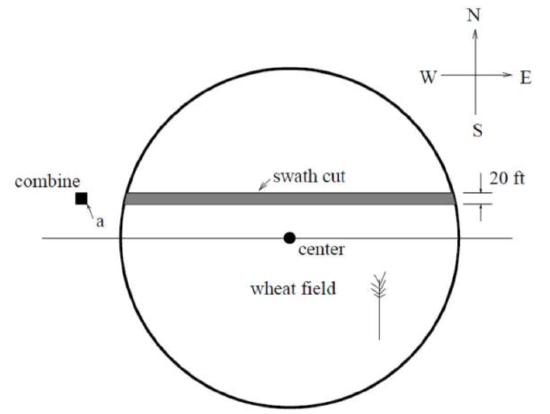 Nora spends part of her summer driving a combine during the wheat harvest. Assume she starts at the indicated position heading east at 10 ft/sec toward a circular wheat field of radius 200 ft. The combine cuts a swath 20 feet wide and begins when the corner of the machine labeled “a” is 60 feet north and 60 feet west of the western-most edge of the field. [UW]
Nora spends part of her summer driving a combine during the wheat harvest. Assume she starts at the indicated position heading east at 10 ft/sec toward a circular wheat field of radius 200 ft. The combine cuts a swath 20 feet wide and begins when the corner of the machine labeled “a” is 60 feet north and 60 feet west of the western-most edge of the field. [UW]
a. When does Nora’s combine first start cutting the wheat?
b. When does Nora’s combine first start cutting a swath 20 feet wide?
c. Find the total amount of time wheat is being cut during this pass across the field.
d. Estimate the area of the swath cut during this pass across the field.
23. The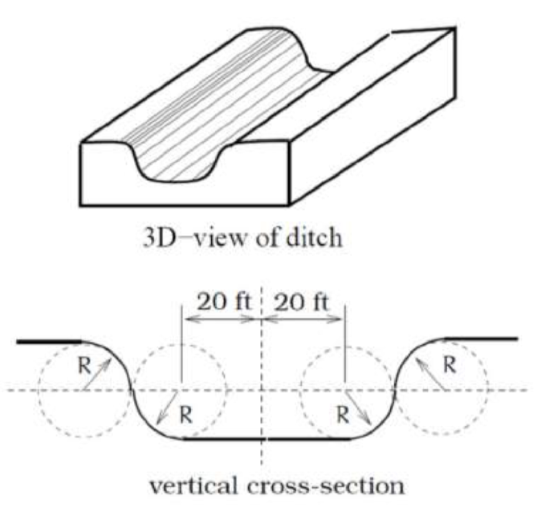 vertical cross-section of a drainage ditch is pictured to the right. Here, R indicates in each case the radius of a circle with R = 10 feet, where all of the indicated circle centers lie along a horizontal line 10 feet above and parallel to the ditch bottom. Assume that water is flowing into the ditch so that the level above the bottom is rising at a rate of 2 inches per minute. [UW]
vertical cross-section of a drainage ditch is pictured to the right. Here, R indicates in each case the radius of a circle with R = 10 feet, where all of the indicated circle centers lie along a horizontal line 10 feet above and parallel to the ditch bottom. Assume that water is flowing into the ditch so that the level above the bottom is rising at a rate of 2 inches per minute. [UW]
a. When will the ditch be completely full?
b. Find a piecewise defined function that models the vertical cross-section of the ditch.
c. What is the width of the filled portion of the ditch after 1 hour and 18 minutes?
d. When will the filled portion of the ditch be 42 feet wide? 50 feet wide? 73 feet wide?
- Answer
-
1. 10
3. \((x - 8)^2 + (y + 10)^2 = 8^2\)
5. \((x - 7)^2 + (y + 2)^2 = 293\)
7. \((x - 5)^2. + (y - 8)^2 = 13\)
9.
11. \((0, 3 + \sqrt{5})\) and \((0, 3 - \sqrt{5})\)
13. (1.3416407865, 7.683281573)
15. (-1.07335, 2.8533)
17. 29.87 miles


