2.1E: Linear Functions (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Section 2.1 exercise
1. A town's population has been growing linearly. In 2003, the population was 45,000, and the population has been growing by 1700 people each year. Write an equation,
P(t), for the population t years after 2003.
2. A town's population has been growing linearly. In 2005, the population was 69,000, and the population has been growing by 2500 people each year. Write an equation,
P(t), for the population t years after 2005.
3. Sonya is currently 10 miles from home, and is walking further away at 2 miles per hour. Write an equation for her distance from home t hours from now.
4. A boat is 100 miles away from the marina, sailing directly towards it at 10 miles per hour. Write an equation for the distance of the boat from the marina after t hours.
5. Timmy goes to the fair with $40. Each ride costs $2. How much money will he have left after riding n rides?
6. At noon, a barista notices she has $20 in her tip jar. If she makes an average of $0.50 from each customer, how much will she have in her tip jar if she serves n more customers during her shift?
Determine if each function is increasing or decreasing
7. f(x)=4x+3
8. g(x)=5x+6
9. a(x)=−2x+4
10. b(x)=8−3x
11. h(x)=−2x+4
12. h(x)=−4x+1
13. j(x)=12x−3
14. p(x)=14x−5
15. n(x)=−13x−2
16. m(x)=−38x+3
Find the slope of the line that passes through the two given points
17. (2, 4) and (4, 10)
18. (1, 5) and (4, 11)
19. (-1, 4) and (5, 2)
20. (-2, 8) and (4, 6)
21. (6, 11) and (-4, 3)
22. (9, 10) and (-6, -12)
Find the slope of the lines graphed
23. 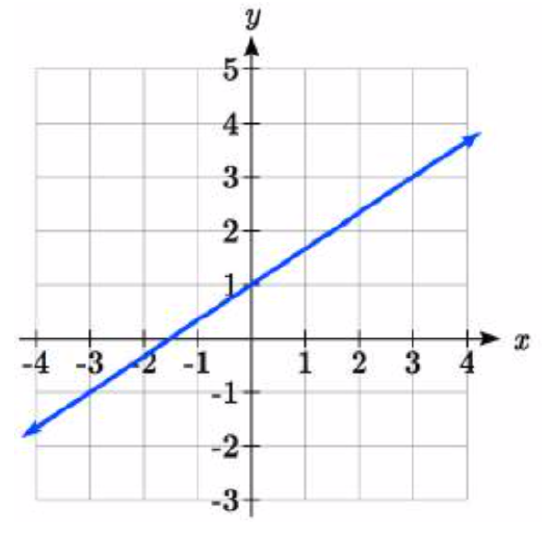 24.
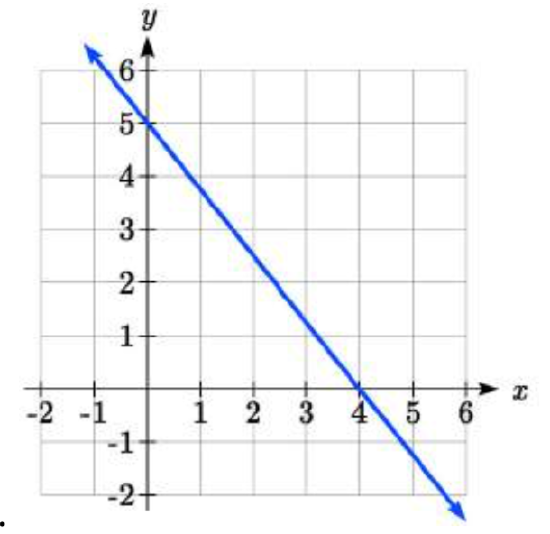
24. 
25. Sonya is walking home from a friend’s house. After 2 minutes she is 1.4 miles from home. Twelve minutes after leaving, she is 0.9 miles from home. What is her rate?
26. A gym membership with two personal training sessions costs $125, while gym membership with 5 personal training sessions costs $260. What is the rate for personal training sessions?
27. A city's population in the year 1960 was 287,500. In 1989 the population was 275,900. Compute the slope of the population growth (or decline) and make a statement about the population rate of change in people per year.
28. A city's population in the year 1958 was 2,113,000. In 1991 the population was 2,099,800. Compute the slope of the population growth (or decline) and make a statement about the population rate of change in people per year.
29. A phone company charges for service according to the formula: C(n)=240.+1n, where n is the number of minutes talked, and C(n) is the monthly charge, in dollars. Find and interpret the rate of change and initial value.
30. A phone company charges for service according to the formula: C(n)=260.+04n, where n is the number of minutes talked, and C(n) is the monthly charge, in dollars. Find and interpret the rate of change and initial value.
31. Terry is skiing down a steep hill. Terry's elevation, E(t), in feet after t seconds is given by E(t)=3000−70t.Write a complete sentence describing Terry’s starting elevation and how it is changing over time.
32. Maria is climbing a mountain. Maria's elevation, E(t), in feet after t minutes is given by E(t)=1200+40t. Write a complete sentence describing Maria’s starting elevation and how it is changing over time.
Given each set of information, find a linear equation satisfying the conditions, if possible
33. f(−5)=−4, and f(5)=2
34. f(−1)=4, and f(5)=1
35. Passes through (2, 4) and (4, 10)
36. Passes through (1, 5) and (4, 11)
37. Passes through (-1, 4) and (5, 2)
38. Passes through (-2, 8) and (4, 6)
39. x intercept at (-2, 0) and y intercept at (0, -3)
40. x intercept at (-5, 00 and y intercept at (0, 4)
Find an equation for the function graphed
41. 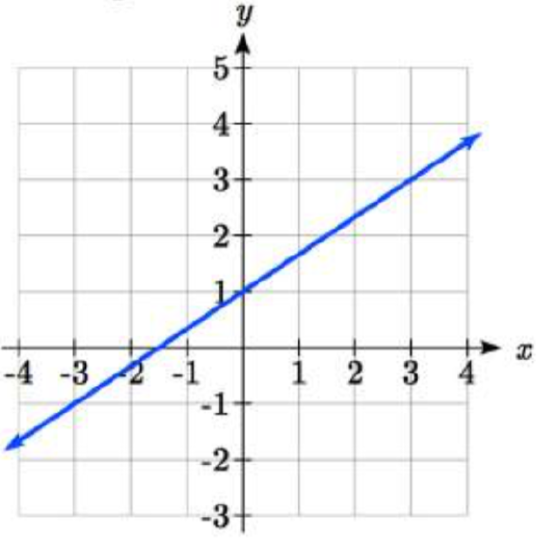 42.
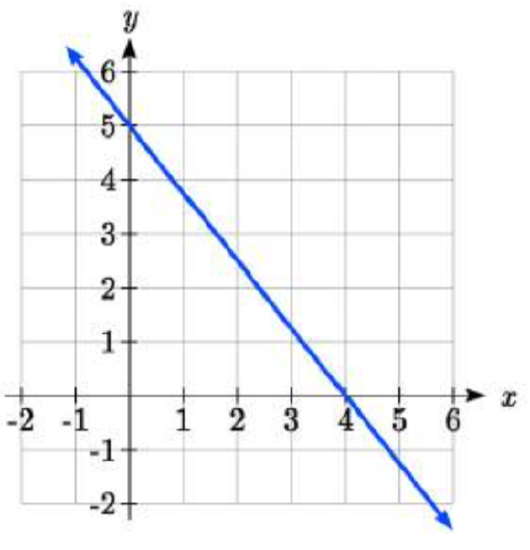
42. 
43. 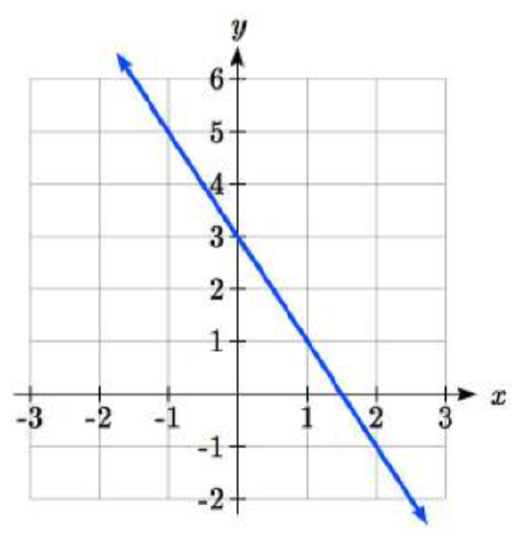 44.
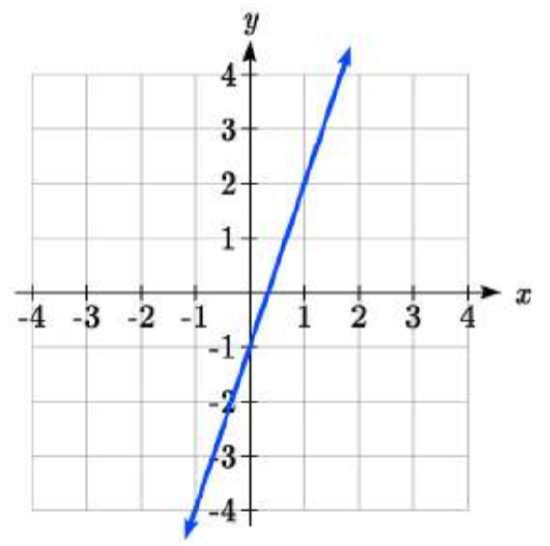
44. 
45. A clothing business finds there is a linear relationship between the number of shirts, n, it can sell and the price, p, it can charge per shirt. In particular, historical data shows that 1000 shirts can be sold at a price of $30, while 3000 shirts can be sold at a price of $22 . Find a linear equation in the form p=mn+b that gives the price p they can charge for n shirts.
46. A farmer finds there is a linear relationship between the number of bean stalks, n, she plants and the yield, y, each plant produces. When she plants 30 stalks, each plant yields 30 oz of beans. When she plants 34 stalks, each plant produces 28 oz of beans. Find a linear relationships in the form y=mn+b that gives the yield when n stalks are planted.
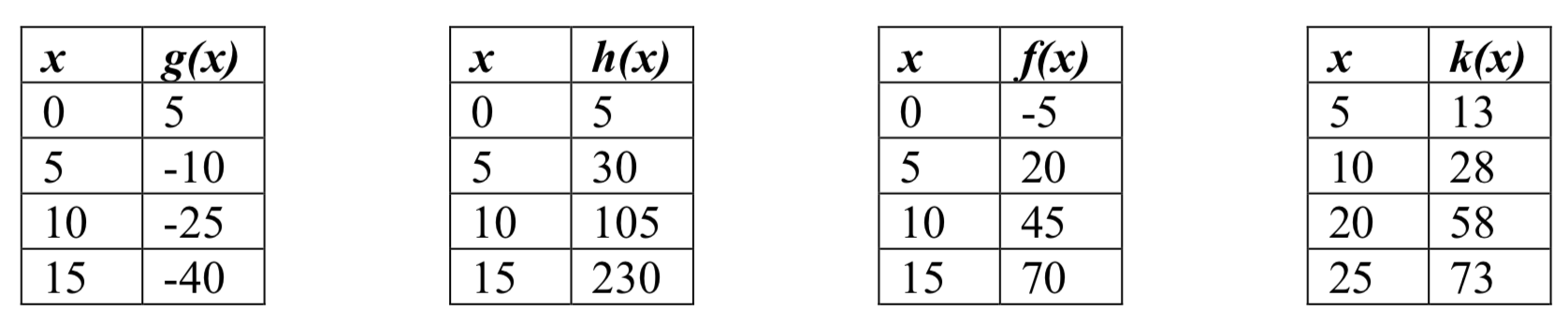
47. Which of the following tables could represent a linear function? For each that could be linear, find a linear equation models the data.
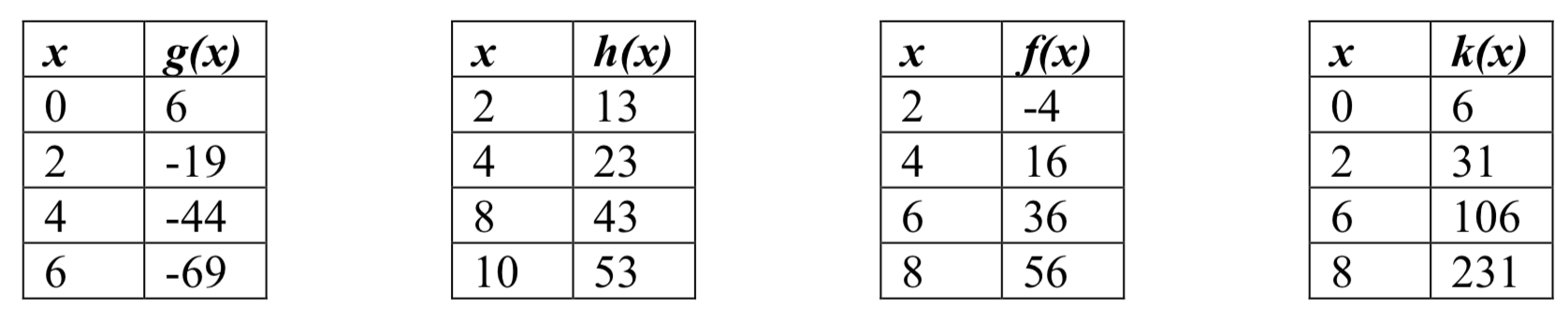
48. Which of the following tables could represent a linear function? For each that could be linear, find a linear equation models the data.
49. While speaking on the phone to a friend in Oslo, Norway, you learned that the current temperature there was -23 Celsius (-23oC). After the phone conversation, you wanted to convert this temperature to Fahrenheit degrees, oF, but you could not find a reference with the correct formulas. You then remembered that the relationship between oF and oC is linear. [UW]
Using this and the knowledge that 32oF = 0 oC and 212 oF = 100 oC, find an equation that computes Celsius temperature in terms of Fahrenheit; i.e. an equation of the form C = “an expression involving only the variable F.”
Likewise, find an equation that computes Fahrenheit temperature in terms of Celsius temperature; i.e. an equation of the form F = “an expression involving only the variable C.”
How cold was it in Oslo in oF?
- Answer
-
1. P(t)=1700t+45000
3. D(t)=10+2t
5. M(n)=40−2n
7. Increasing
9. Decreasing
11. Decreasing
13. Increasing
15. Decreasing
17. 3
19. −13
21. 43
23. 23
25. -0.05 mph (or 0.05 miles per hour toward her home)
27. Population is decreasing by 400 people per year
29. Monthly charge in dollars has an initial base charge of $24, and increases by $0.10 for each minute talked
31. Terry started at an elevation of 3,000 ft and is descending by 70ft per second.
33. y=35x−1
35. y=3x−2
37. y=−13x+113
39. y=−1.5x−3
41. y=23x+1
43. y=−2x+3
45. P(n)=−0.004n+34
47. The 1st, 3rd & 4th tables are linear: respectively
1. g(x)=−3x+5
3. f(x)=5x−5
4. k(x)=3x−249a. C=59F−1609
b. F=95C+32
c. −9.4∘F


