2.2: Graphs of Linear Functions
- Page ID
- 13835
When we are working with a new function, it is useful to know as much as we can about the function: its graph, where the function is zero, and any other special behaviors of the function. We will begin this exploration of linear functions with a look at graphs.
When graphing a linear function, there are three basic ways to graph it:
- By plotting points (at least 2) and drawing a line through the points
- Using the initial value (output when x = 0) and rate of change (slope)
- Using transformations of the identity function \(f(x)=x\)
Example \(\PageIndex{1}\)
Graph \(f(x)=5-\dfrac{2}{3} x\) by plotting points.
Solution
In general, we evaluate the function at two or more inputs to find at least two points on the graph. Usually it is best to pick input values that will “work nicely” in the equation. In this equation, multiples of 3 will work nicely due to the \(\dfrac{2}{3}\) in the equation, and of course using \(x = 0\) to get the vertical intercept. Evaluating \(f(x)\) at \(x = 0\), 3 and 6: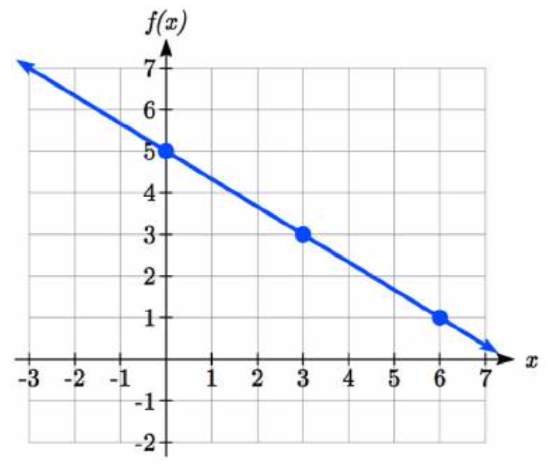
\[f(0) = 5 - \dfrac{2}{3} (0) = 5\nonumber \]
\[f(3) = 5 - \dfrac{2}{3} (3) = 3\nonumber \]
\[f(6) = 5 - \dfrac{2}{3} (6) = 1\nonumber \]
These evaluations tell us that the points (0,5), (3,3), and (6,1) lie on the graph of the line. Plotting these points and drawing a line through them gives us the graph.
When using the initial value and rate of change to graph, we need to consider the graphical interpretation of these values. Remember the initial value of the function is the output when the input is zero, so in the equation \(f(x)=b+mx\), the graph includes the point \((0, b)\). On the graph, this is the vertical intercept – the point where the graph crosses the vertical axis.
For the rate of change, it is helpful to recall that we calculated this value as
\[m = \dfrac{change\ of\ output}{change\ of\ input}\nonumber\]
From a graph of a line, this tells us that if we divide the vertical difference, or rise, of the function outputs by the horizontal difference, or run, of the inputs, we will obtain the rate of change, also called slope of the line.
\[m=\dfrac{change\ of \ output}{change\ of\ input} = \dfrac{rise}{run}\nonumber \]
Notice that this ratio is the same regardless of which two points we use.
Definition: Graphical interpretation of a linear equation
Graphically, in the equation\(f(x)=b+mx\),
\(b\) is the vertical intercept of the graph and tells us we can start our graph at (0, b)
\(m\) is the slope of the line and tells us how far to rise & run to get to the next point
Once we have at least 2 points, we can extend the graph of the line to the left and right.
Example \(\PageIndex{2}\)
Graph \(f(x)=5-\dfrac{2}{3} x\) using the vertical intercept and slope.
Solution
The vertical intercept of the function is (0, 5), giving us a point on the graph of the line.
The slope is \(-\dfrac{2}{3}\). This tells us that for every 3 units the graph “runs” in the horizontal, the vertical “rise” decreases by 2 units.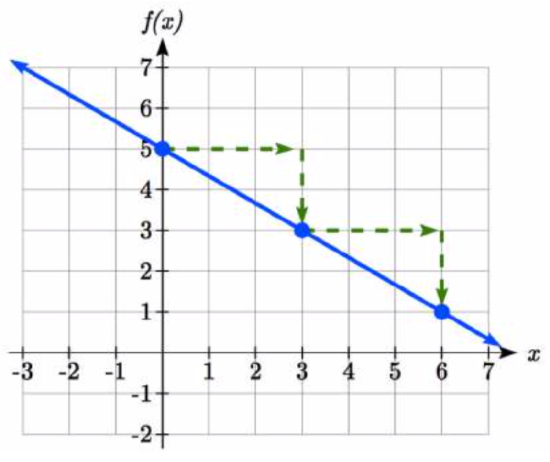
In graphing, we can use this by first plotting our vertical intercept on the graph, then using the slope to find a second point. From the initial value (0, 5) the slope tells us that if we move to the right 3, we will move down 2, moving us to the point (3, 3). We can continue this again to find a third point at (6, 1). Finally, extend the line to the left and right, containing these points.
Exercise \(\PageIndex{1}\)
Consider that the slope \(-\dfrac{2}{3}\) could also be written as \(\dfrac{2}{-3}\). Using \(\dfrac{2}{-3}\), find another point on the graph that has a negative \(x\) value.
- Answer
-
\((-3,7)\) found by starting at the vertical intercept, going up \(2\) units and \(3\) in the negative horizontal direction. You could have also answered, \((-6, 9)\) or \((-9, 11)\) etc…
Another option for graphing is to use transformations of the identity function\(f(x)=x\).
In the equation\(f(x)=mx\), the m is acting as the vertical stretch of the identity function. When \(m\) is negative, there is also a vertical reflection of the graph. Looking at some examples:
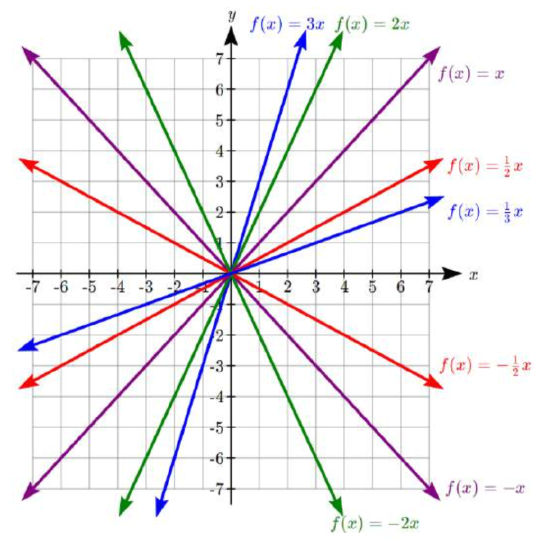
In\(f(x)=mx+b\), the b acts as the vertical shift, moving the graph up and down without affecting the slope of the line. Some examples:
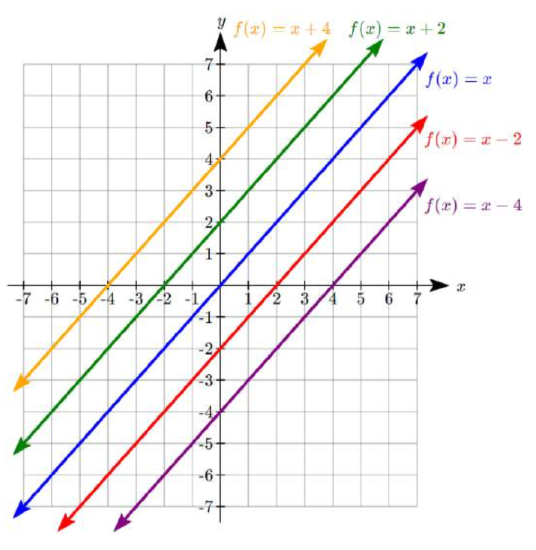
Using Vertical Stretches or Compressions along with Vertical Shifts is another way to look at identifying different types of linear functions. Although this may not be the easiest way for you to graph this type of function, make sure you practice each method.
Example \(\PageIndex{3}\)
Graph \(f(x)=-3+\dfrac{1}{2} x\) using transformations.
Solution
The equation is the graph of the identity function vertically compressed by ½ and vertically shifted down 3.
Vertical Compression combined with Vertical shift
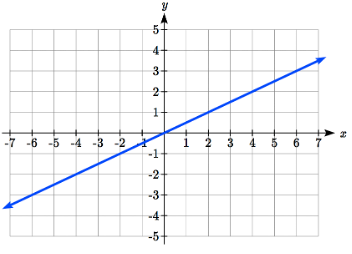
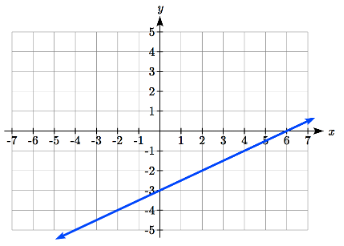
Notice how this nicely compares to the other method where the vertical intercept is found at (0, -3) and to get to another point we rise (go up vertically) by 1 unit and run (go horizontally) by 2 units to get to the next point (2, -2), and the next one (4, -1). In these three points (0, -3), (2, -2), and (4, -1), the output values change by +1, and the \(x\) values change by +2, corresponding with the slope \(m = 1/2\).
Example \(\PageIndex{4}\)
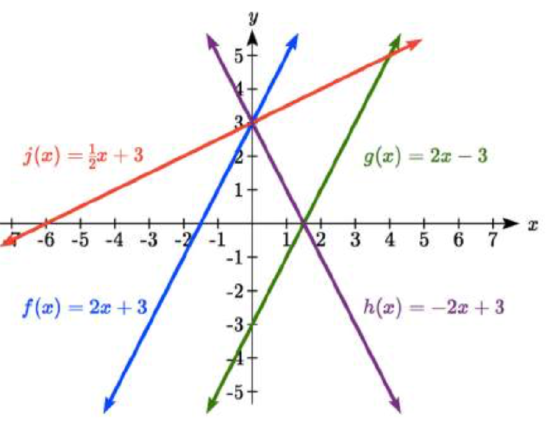
Match each equation with one of the lines in the graph below
\[f(x) = 2x + 3\nonumber \]
\[g(x) = 2x - 3\nonumber \]
\[(h(x) = -2x = 3\nonumber \]
\[j(x) = \dfrac{1}{2} x + 3\nonumber \]
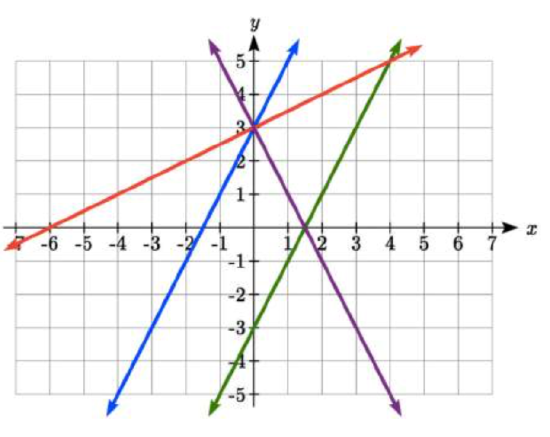
Solution
Only one graph has a vertical intercept of - 3, so we can immediately match that graph with \(g(x)\).
For the three graphs with a vertical intercept at 3, only one has a negative slope, so we can match that line with \(h(x)\). Of the other two, the steeper line would have a larger slope, so we can match that graph with equation \(f(x)\), and the flatter line with the equation \(j(x)\).
In addition to understanding the basic behavior of a linear function (increasing or decreasing, recognizing the slope and vertical intercept), it is often helpful to know the horizontal intercept of the function – where it crosses the horizontal axis.
Definition: Finding Horizontal intercepts
The horizontal intercept of the function is where the graph crosses the horizontal axis. If a function has a horizontal intercept, you can always find it by solving \(f(x) = 0\).
Example \(\PageIndex{5}\)
Find the horizontal intercept of \(f(x)=-3+\dfrac{1}{2} x\)
Solution
Setting the function equal to zero to find what input will put us on the horizontal axis,
\[\begin{array} {rcl} {0} &= & {-3 + \dfrac{1}{2}x} \\ {3} &= & {\dfrac{1}{2} x} \\ {x} &= & {6} \end{array}\nonumber\]
The graph crosses the horizontal axis at (6,0)
There are two special cases of lines: a horizontal line and a vertical line. In a horizontal line like the one graphed to the right, notice that between any two points, the change in the outputs is 0. In the slope equation, the numerator will be 0, resulting in a slope of 0. Using a slope of 0 in the \(f(x)=b+mx\), the equation simplifies to \(f(x)=b\).
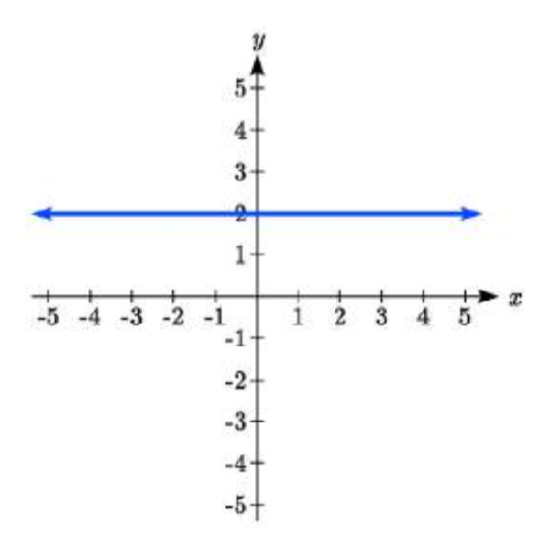
Notice a horizontal line has a vertical intercept, but no horizontal intercept (unless it’s the line \(f(x) = 0\)).
In the case of a vertical line, notice that between any two points, the change in the inputs is zero. In the slope equation, the denominator will be zero, and you may recall that we cannot divide by the zero; the slope of a vertical line is undefined. You might also notice that a vertical line is not a function. To write the equation of vertical line, we simply write input=value, like \(x = b\).
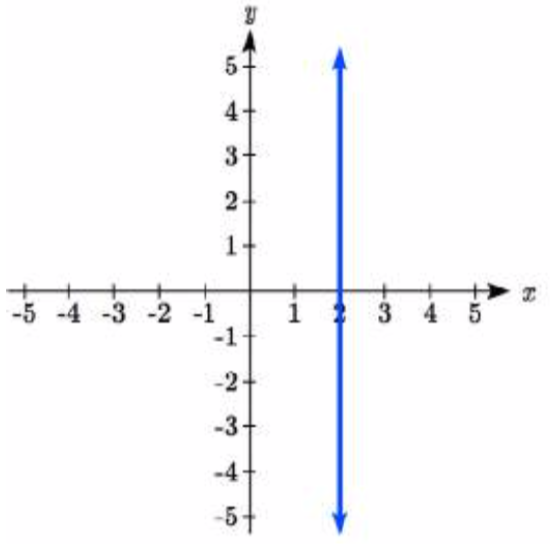
Notice a vertical line has a horizontal intercept, but no vertical intercept (unless it’s the line \(x = 0\)).
Definition: horizontal and vertical lines
Horizontal lines have equations of the form \(f(x)=b\)
Vertical lines have equations of the form \(x = a\)
Example \(\PageIndex{6}\)
Write an equation for the horizontal line graphed above.
Solution
This line would have equation \(f(x)=2\)
Example \(\PageIndex{7}\)
Write an equation for the vertical line graphed above.
Solution
This line would have equation \(x=2\)
Exercise \(\PageIndex{2}\)
Describe the function \(f(x)=6-3x\) in terms of transformations of the identity function and find its horizontal intercept.
- Answer
-
Vertically stretched by a factor of 3, Vertically flipped (flipped over the \(x\) axis),
Vertically shifted up by 6 units.
Horizontal intercept: \(6 - 3x = 0\) when \(x=2\).
Parallel and Perpendicular Lines
When two lines are graphed together, the lines will be parallel if they are increasing at the same rate – if the rates of change are the same. In this case, the graphs will never cross (unless they’re the same line).
Definition: Parallel lines
Two lines are parallel if the slopes are equal (or, if both lines are vertical).
In other words, given two linear equations \(f(x)=b+m_{1} x\) and \(g(x)=b+m_{2} x\), the lines will be parallel if \(m_{1} =m_{2}\).
Example \(\PageIndex{8}\)
Find a line parallel to \(f(x)=6+3x\) that passes through the point (3, 0).
Solution
We know the line we’re looking for will have the same slope as the given line, \(m = 3\). Using this and the given point, we can solve for the new line’s vertical intercept:
\[g(x) = b + 3x\nonumber\] then at (3, 0),
\[0 = b + 3(3)\nonumber \]
\[b = -9\nonumber \]
The line we’re looking for is \(g(x)=-9+3x\).
If two lines are not parallel, one other interesting possibility is that the lines are perpendicular, which means the lines form a right angle (90 degree angle – a square corner) where they meet. In this case, the slopes when multiplied together will equal -1. Solving for one slope leads us to the definition:
Definition: Perpendicular lines
Given two linear equations \(f(x)=b+m_{1} x\) and \(g(x)=b+m_{2} x\)
The lines will be perpendicular if \(m_{1} m_{2} =-1\), and so \(m_{2} =\dfrac{-1}{m_{1} }\)
We often say the slope of a perpendicular line is the “negative reciprocal” of the other line’s slope.
Example \(\PageIndex{9}\)
Find the slope of a line perpendicular to a line with:
a) a slope of 2. b) a slope of -4. c) a slope of \(\dfrac{2}{3}\).
Solution
If the original line had slope 2, the perpendicular line’s slope would be \(m_{2} =\dfrac{-1}{2}\)
If the original line had slope -4, the perpendicular line’s slope would be \(m_{2} =\dfrac{-1}{-4} =\dfrac{1}{4}\)
If the original line had slope \(\dfrac{2}{3}\), the perpendicular line’s slope would be \(m_2 = \dfrac{-1}{2/3} = \dfrac{-3}{2}\)
Example \(\PageIndex{10}\)
Find the equation of a line perpendicular to \(f(x)=6+3x\) and passing through the point (3, 0).
Solution
The original line has slope m = 3. The perpendicular line will have slope \(m=\dfrac{-1}{3}\). Using this and the given point, we can find the equation for the line.
\[g(x)=b-\dfrac{1}{3} x\nonumber \] then at (3, 0),
\[0 = b - \dfrac{1}{3} (3)\nonumber \]
\[b = 1\nonumber \]
The line we’re looking for is \(g(x)=1-\dfrac{1}{3} x\).
Exercise \(\PageIndex{3}\)
Given the line \(h(t)=-4+2t\), find an equation for the line passing through (0, 0) that is:
- parallel to h(t).
- perpendicular to h(t).
- Answer
-
Parallel: \(f(t)=2t\)
Perpendicular: \(g(t)=-\dfrac{1}{2} t\)
Example \(\PageIndex{12}\)
A line passes through the points (-2, 6) and (4, 5). Find the equation of a perpendicular line that passes through the point (4, 5).
Solution
From the two given points on the reference line, we can calculate the slope of that line:
\[m_1 = \dfrac{5-6}{4 - (-2)} = \dfrac{-1}{6}\nonumber \]
The perpendicular line will have slope
\[m_2 = \dfrac{-1}{-1/6} = 6\nonumber \]
We can then solve for the vertical intercept that makes the line pass through the desired point:
\[g(x) = b + 6x\nonumber \] then at (4, 5)
\[5 = b + 6(4)\nonumber \]
\[b = -19\nonumber \]
Giving the line \(g(x)=-19+6x\)
Intersections of Lines
The graphs of two lines will intersect if they are not parallel. They will intersect at the point that satisfies both equations. To find this point when the equations are given as functions, we can solve for an input value so that \(f(x)=g(x)\). In other words, we can set the formulas for the lines equal, and solve for the input that satisfies the equation.
Example \(\PageIndex{13}\)
Find the intersection of the lines \(h(t)=3t-4\) and \(j(t)=5-t\).
Solution
Setting \(h(t)=j(t)\),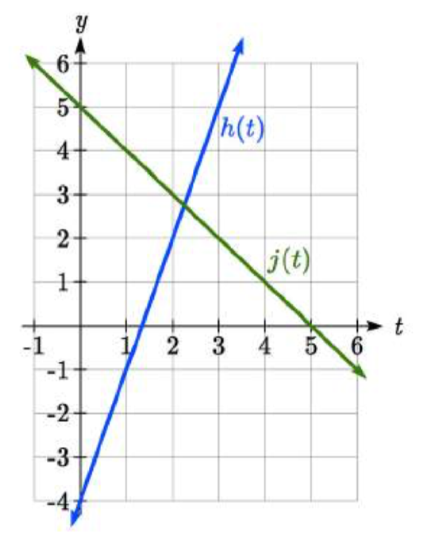
\[\begin{array} {rcl} {3t - 4} &= & {5 - t} \\ {4t} &= & {9} \\ {t} &= & {\dfrac{9}{4}} \end{array}\nonumber \]
This tells us the lines intersect when the input is \(\dfrac{9}{4}\).
We can then find the output value of the intersection point by evaluating either function at this input
\[j(\dfrac{9}{4} )=5-\dfrac{9}{4} =\dfrac{11}{4}\nonumber \]
These lines intersect at the point \((\dfrac{9}{4} ,\dfrac{11}{4} )\). Looking at the graph, this result seems reasonable.
Two parallel lines can also intersect if they happen to be the same line. In that case, they intersect at every point on the lines.
Exercise \(\PageIndex{4}\)
Look at the graph in example 13 above and answer the following for the function \(h(t)\):
a. Vertical intercept coordinates
b. Horizontal intercepts coordinates
c. Slope
d. Is \(j(t)\) parallel or perpendicular to \(h(t)\) (or neither)
e. Is h(t) an Increasing or Decreasing function (or neither)
f. Write a transformation description from the identity toolkit function \(f(x) = x\)
- Answer
-
4. Given \(h(t)=3t-4\)
a. (0,-4)
b. \((\dfrac{4}{3} ,0)\)
c. Slope 3
d. Neither parallel nor perpendicular
e. Increasing function
f. Given the identity function, vertically stretch by 3 and shift down 4 units.
Finding the intersection allows us to answer other questions as well, such as discovering when one function is larger than another.
Example \(\PageIndex{14}\)
Using the functions from the previous example, for what values of t is \(h(t) > j(t)\).
Solution
To answer this question, it is helpful first to know where the functions are equal, since that is the point where \(h(t)\) could switch from being greater to smaller than \(j(t)\) or vice-versa. From the previous example, we know the functions are equal at \(t=\dfrac{9}{4}\).
By examining the graph, we can see that \(h(t)\), the function with positive slope, is going to be larger than the other function to the right of the intersection. So \(h(t) > j(t)\) when \(t > \dfrac{9}{4}\)
Important Topics of this Section
- Methods for graphing linear functions
- Another name for slope = rise/run
- Horizontal intercepts (a,0)
- Horizontal lines
- Vertical lines
- Parallel lines
- Perpendicular lines
- Intersecting lines


