6.5E: Modeling with Trigonometric Functions (Exercises)
- Page ID
- 13927
section 6.5 exercises
In each of the following triangles, solve for the unknown side and angles.
1. 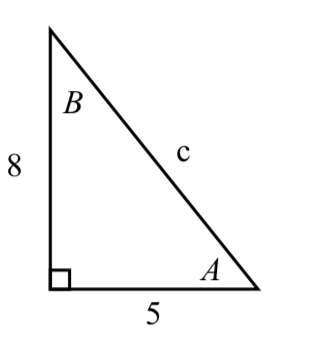 2.
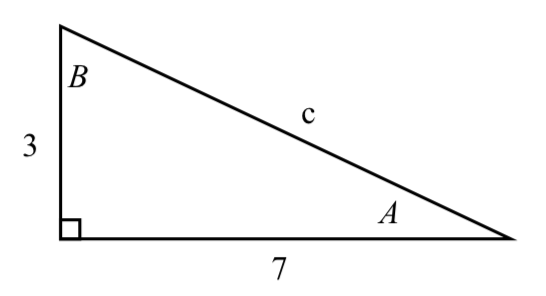
2.
3. 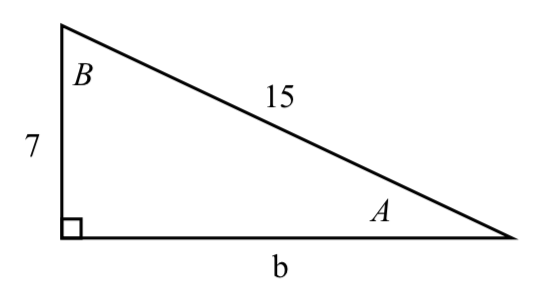 4.
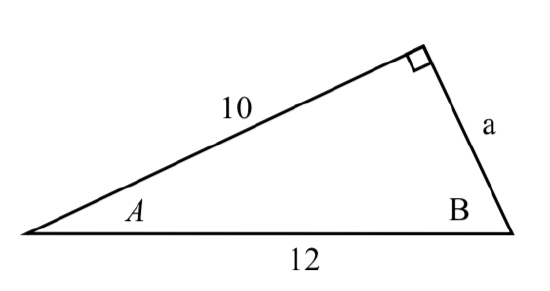
4.
Find a possible formula for the trigonometric function whose values are in the following tables.
5.
| \(x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| \(y\) | -2 | 4 | 10 | 4 | -2 | 4 | 10 |
6.
| \(x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| \(y\) | 1 | -3 | -7 | -3 | 1 | -3 | -7 |
7. Outside temperature over the course of a day can be modeled as a sinusoidal function. Suppose you know the high temperature for the day is 63 degrees and the low temperature of 37 degrees occurs at 5 AM. Assuming \(t\) is the number of hours since midnight, find an equation for the temperature, \(D\), in terms of \(t\).
8. Outside temperature over the course of a day can be modeled as a sinusoidal function. Suppose you know the high temperature for the day is 92 degrees and the low temperature of 78 degrees occurs at 4 AM. Assuming \(t\) is the number of hours since midnight, find an equation for the temperature, \(D\), in terms of \(t\).
9. A population of rabbits oscillates 25 above and below an average of 129 during the year, hitting the lowest value in January (\(t = 0\)).
a. Find an equation for the population, \(P\), in terms of the months since January, \(t\).
b. What if the lowest value of the rabbit population occurred in April instead?
10. A population of elk oscillates 150 above and below an average of 720 during the year, hitting the lowest value in January (\(t = 0\)).
a. Find an equation for the population, \(P\), in terms of the months since January, \(t\).
b. What if the lowest value of the rabbit population occurred in March instead?
11. Outside temperature over the course of a day can be modeled as a sinusoidal function. Suppose you know the high temperature of 105 degrees occurs at 5 PM and the average temperature for the day is 85 degrees. Find the temperature, to the nearest degree, at 9 AM.
12. Outside temperature over the course of a day can be modeled as a sinusoidal function. Suppose you know the high temperature of 84 degrees occurs at 6 PM and the average temperature for the day is 70 degrees. Find the temperature, to the nearest degree, at 7 AM.
13. Outside temperature over the course of a day can be modeled as a sinusoidal function. Suppose you know the temperature varies between 47 and 63 degrees during the day and the average daily temperature first occurs at 10 AM. How many hours after midnight does the temperature first reach 51 degrees?
14. Outside temperature over the course of a day can be modeled as a sinusoidal function. Suppose you know the temperature varies between 64 and 86 degrees during the day and the average daily temperature first occurs at 12 AM. How many hours after midnight does the temperature first reach 70 degrees?
15. A Ferris wheel is 20 meters in diameter and boarded from a platform that is 2 meters above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 6 minutes. How many minutes of the ride are spent higher than 13 meters above the ground?
16. A Ferris wheel is 45 meters in diameter and boarded from a platform that is 1 meter above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 10 minutes. How many minutes of the ride are spent higher than 27 meters above the ground?
17. The sea ice area around the North Pole fluctuates between about 6 million square kilometers in September to 14 million square kilometers in March. Assuming sinusoidal fluctuation, during how many months are there less than 9 million square kilometers of sea ice?
18. The sea ice area around the South Pole fluctuates between about 18 million square kilometers in September to 3 million square kilometers in March. Assuming sinusoidal fluctuation, during how many months are there more than 15 million square kilometers of sea ice?
19. A respiratory ailment called “Cheyne-Stokes Respiration” causes the volume per breath to increase and decrease in a sinusoidal manner, as a function of time. For one particular patient with this condition, a machine begins recording a plot of volume per breath versus time (in seconds). Let \(b(t)\) be a function of time t that tells us the volume (in liters) of a breath that starts at time \(t\). During the test, the smallest volume per breath is 0.6 liters and this first occurs for a breath that starts 5 seconds into the test. The largest volume per breath is 1.8 liters and this first occurs for a breath beginning 55 seconds into the test. [UW]
a. Find a formula for the function \(b(t)\) whose graph will model the test data for this patient.
b. If the patient begins a breath every 5 seconds, what are the breath volumes during the first minute of the test?
20. Suppose the high tide in Seattle occurs at 1:00 a.m. and 1:00 p.m, at which time the water is 10 feet above the height of low tide. Low tides occur 6 hours after high tides. Suppose there are two high tides and two low tides every day and the height of the tide varies sinusoidally. [UW]
a. Find a formula for the function \(y = h(t)\) that computes the height of the tide above low tide at time \(t\). (In other words, \(y = 0\) corresponds to low tide.)
b. What is the tide height at 11:00 a.m.?
21. A communications satellite orbits the earth \(t\) miles above the surface. Assume the r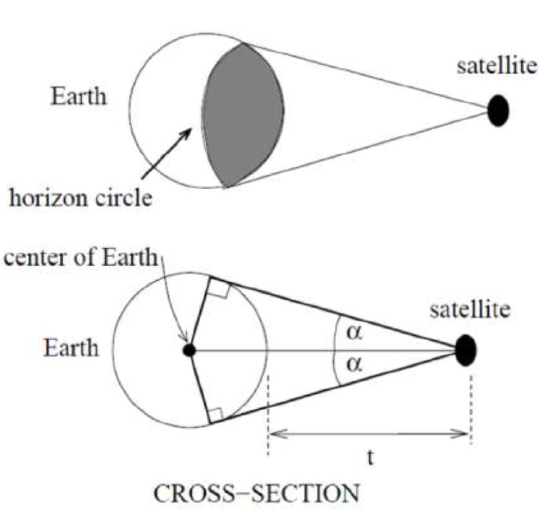 adius of the earth is 3,960 miles. The satellite can only “see” a portion of the earth’s surface, bounded by what is called a horizon circle. This leads to a two-dimensional cross-sectional picture we can use to study the size of the horizon slice: [UW]
adius of the earth is 3,960 miles. The satellite can only “see” a portion of the earth’s surface, bounded by what is called a horizon circle. This leads to a two-dimensional cross-sectional picture we can use to study the size of the horizon slice: [UW]
a. Find a formula for \(\alpha\) in terms of \(t\).
b. If \(t = 30,000\) miles, what is \(\alpha\)? What percentage of the circumference of the earth is covered by the satellite? What would be the minimum number of such satellites required to cover the circumference?
c. If \(t = 1,000\) miles, what is \(\alpha\)? What percentage of the circumference of the earth is covered by the satellite? What would be the minimum number of such satellites required to cover the circumference?
d. Suppose you wish to place a satellite into orbit so that 20% of the circumference is covered by the satellite. What is the required distance \(t\)?
22. Tiffany is a model rocket enthusiast. She has been working on a pressurized rocket filled with nitrous oxide. According to her design, if the atmospheric pressure exerted on the rocket is less than 10 pounds/sq.in., the nitrous oxide chamber inside the rocket will explode. Tiff worked from a formula \(p=14.7e^{-h/10}\) pounds/sq.in. for the atmospheric pressure \(h\) miles above sea level. Assume that the rocket is launched at an angle of \(\alpha\) above level ground at sea level with an initial speed of 1400 feet/sec. Also, assume the height (in feet) of the rocket at time \(t\) seconds is given by the equation \(y\left(t\right)=-16t^{2} +1400\sin \left(\alpha \right)t\). [UW]
a. At what altitude will the rocket explode?
b. If the angle of launch is \(\alpha\) = 12\(\mathrm{{}^\circ}\), determine the minimum atmospheric pressure exerted on the rocket during its flight. Will the rocket explode in midair?
c. If the angle of launch is \(\alpha\) = 82\(\mathrm{{}^\circ}\), determine the minimum atmospheric pressure exerted on the rocket during its flight. Will the rocket explode in midair?
d. Find the largest launch angle \(\alpha\) so that the rocket will not explode.
- Answer
-
1. \(c = \sqrt{89}\), \(A = 57.9946^{\circ}\), \(B = 32.0054^{\circ}\)
3. \(b = \sqrt{176}\), \(A = 27.8181^{\circ}\), \(B = 62.1819^{\circ}\)
5. \(y(x) = 6 \sin (\dfrac{\pi}{2}(x - 1)) + 4\)
7. \(D(t) = 50 - 13 \cos(\dfrac{\pi}{12}(t - 5))\)
9. a. \(P(t) = 129 - 25 \cos(\dfrac{\pi}{6} t)\)
b. \(P(t) = 129 - 25 \cos(\dfrac{\pi}{6} (t - 3))\)11. 75 degrees
13. 8
15. 2.80869431742
17. 5.035 months


