4.E: Exponential and Logarithmic Functions (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
4.1: Exponential Functions
When populations grow rapidly, we often say that the growth is “exponential,” meaning that something is growing very rapidly. To a mathematician, however, the term exponential growth has a very specific meaning. In this section, we will take a look at exponential functions, which model this kind of rapid growth.
Verbal
1) Explain why the values of an increasing exponential function will eventually overtake the values of an increasing linear function.
- Answer:
-
Linear functions have a constant rate of change. Exponential functions increase based on a percent of the original.
2) Given a formula for an exponential function, is it possible to determine whether the function grows or decays exponentially just by looking at the formula? Explain.
3)The Oxford Dictionary defines the word nominal as a value that is “stated or expressed but not necessarily corresponding exactly to the real value.” Develop a reasonable argument for why the term nominal rate is used to describe the annual percentage rate of an investment account that compounds interest.
- Answer:
-
When interest is compounded, the percentage of interest earned to principal ends up being greater than the annual percentage rate for the investment account. Thus, the annual percentage rate does not necessarily correspond to the real interest earned, which is the very definition of nominal.
Algebraic
For the following exercises, identify whether the statement represents an exponential function. Explain.
4) The average annual population increase of a pack of wolves is 25.
5) A population of bacteria decreases by a factor of 18 every 24 hours.
- Answer:
-
exponential; the population decreases by a proportional rate.
6) The value of a coin collection has increased by 3.25%
7) For each training session, a personal trainer charges his clients $5 less than the previous training session.
- Answer:
-
not exponential; the charge decreases by a constant amount each visit, so the statement represents a linear function.
8) The height of a projectile at time t is represented by the function h(t)=−4.9t2+18t+40
For the following exercises, consider this scenario: For each year t, the population of a forest of trees is represented by the function A(t)=115(1.025)t.
9) Which forest’s population is growing at a faster rate?
- Answer:
-
The forest represented by the function B(t)=82(1.029)t.
10) Which forest had a greater number of trees initially? By how many?
11) Assuming the population growth models continue to represent the growth of the forests, which forest will have a greater number of trees after 20 years? By how many?
- Answer:
-
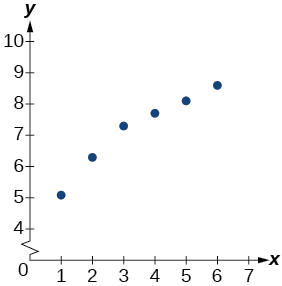
After t=20 years, forest A will have 43
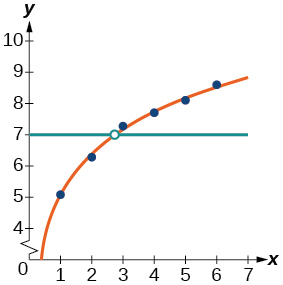
12) Assuming the population growth models continue to represent the growth of the forests, which forest will have a greater number of trees after 100
13) Discuss the above results from the previous four exercises. Assuming the population growth models continue to represent the growth of the forests, which forest will have the greater number of trees in the long run? Why? What are some factors that might influence the long-term validity of the exponential growth model?
- Answer:
-
Answers will vary. Sample response: For a number of years, the population of forest A will increasingly exceed forest B, but because forest B actually grows at a faster rate, the population will eventually become larger than forest A and will remain that way as long as the population growth models hold. Some factors that might influence the long-term validity of the exponential growth model are drought, an epidemic that culls the population, and other environmental and biological factors.
For the following exercises, determine whether the equation represents exponential growth, exponential decay, or neither. Explain.
14) y=300(1−t)5
15) y=220(1.06)x
- Answer:
-
exponential growth; The growth factor, 1.06 is greater than 1.
16) y=16.5(1.025)1x
17) y=11,701(0.97)t
- Answer:
-
exponential decay; The decay factor, 0.97
, .
For the following exercises, find the formula for an exponential function that passes through the two points given.
18) (0,6) and (3,750)
19) (0,2000)
- Answer:
-
f(x)=2000(0.1)x
20) (−1,32) and (3,24)
21) (−2,6)
- Answer:
-
f(x)=(16)−35(16)x5≈2.93(0.699)x
22) (3,1) and (5,4)
For the following exercises, determine whether the table could represent a function that is linear, exponential, or neither. If it appears to be exponential, find a function that passes through the points.
23)
| x | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| f(x) | 70 | 40 | 10 | -20 |
- Answer:
-
Linear
24)
| x | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| h(x) | 70 | 49 | 34.3 | 24.01 |
25)
| x | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| m(x) | 80 | 61 | 42.9 | 25.61 |
- Answer:
-
Neither
26)
| x | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| f(x) | 10 | 20 | 40 | 80 |
27)
| x | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| g(x) | -3.25 | 2 | 7.25 | 12.5 |
- Answer:
-
Linear
For the following exercises, use the compound interest formula, A(t)=P(1+rn)nt
28) After a certain number of years, the value of an investment account is represented by the equation 10,250(1+0.0412)120
29) What was the initial deposit made to the account in the previous exercise?
- Answer:
-
$10,250
30) How many years had the account from the previous exercise been accumulating interest?
31) An account is opened with an initial deposit of $6,500 and earns 3.6% interest compounded semi-annually. What will the account be worth in 20 years?
- Answer:
-
$13,268.58
32) How much more would the account in the previous exercise have been worth if the interest were compounding weekly?
33) Solve the compound interest formula for the principal, P.
- Answer:
-
P=A(t)⋅(1+rn)−nt
34) Use the formula found in the previous exercise to calculate the initial deposit of an account that is worth $14,472.74 after earning 5.5%
35) How much more would the account in the previous two exercises be worth if it were earning interest for 5 more years?
- Answer:
-
$4,572.56
36) Use properties of rational exponents to solve the compound interest formula for the interest rate, r.
37) Use the formula found in the previous exercise to calculate the interest rate for an account that was compounded semi-annually, had an initial deposit of $9,000 and was worth $13,373.53 after 10 years.
- Answer:
-
4%
38) Use the formula found in the previous exercise to calculate the interest rate for an account that was compounded monthly, had an initial deposit of $5,500, and was worth $38,455 after 30 years.
For the following exercises, determine whether the equation represents continuous growth, continuous decay, or neither. Explain.
39) y=3742(e)0.75t
- Answer:
-
continuous growth; the growth rate is greater than 0.
40) y=150(e)3.25t
41) y=2.25(e)−2t
- Answer:
-
continuous decay; the growth rate is less than 0.
42) Suppose an investment account is opened with an initial deposit of $12,000 earning 7.2%
43) How much less would the account from Exercise 42 be worth after 30 years if it were compounded monthly instead?
- Answer:
-
$669.42
Numeric
For the following exercises, evaluate each function. Round answers to four decimal places, if necessary.
44) f(x)=2(5)x for f(−3)
45) f(x)=−42x+3 for f(−1)
- Answer:
-
f(−1)=−4
46) f(x)=ex, for f(3)
47) f(x)=−2ex−1, for f(−1)
- Answer:
-
f(−1)≈−0.2707
48) f(x)=2.7(4)−x+1+1.5, for f(−2)
49) f(x)=1.2e2x−0.3, for f(3)
- Answer:
-
f(3)≈483.8146
50) f(x)=−32(3)−x+32, for f(2)
Technology
For the following exercises, use a graphing calculator to find the equation of an exponential function given the points on the curve.
51) (0,3) and (3,375)
- Answer:
-
y=3⋅5x
52) (3,222.62) and (10,77.456)
53) (20,29.495) and (150,730.89)
- Answer:
-
y≈18⋅1.025x
54) (5,2.909) and (13,0.005)
55) ((11,310.035)\) and (25,356.3652)
- Answer:
-
y≈0.2⋅1.95x
Extensions
56) The annual percentage yield (APY) of an investment account is a representation of the actual interest rate earned on a compounding account. It is based on a compounding period of one year. Show that the APY of an account that compounds monthly can be found with the formula APY=(1+r12)12−1
57) Repeat the previous exercise to find the formula for the APY of an account that compounds daily. Use the results from this and the previous exercise to develop a function I(n)
- Answer:
-
APY=A(t)−aa=a(1+r365)365(1)−aa=a[(1+r365)365−1]a=(1+r365)365−1; I(n)=(1+rn)n−1
58) Recall that an exponential function is any equation written in the form f(x)=a⋅bx such that a and b are positive numbers and b≠1. Any positive number b
59) In an exponential decay function, the base of the exponent is a value between 0 and 1. Thus, for some number b>1,
- Answer:
-
Let f be the exponential decay function f(x)=a⋅(1b)x such that b>1. Then for some number n>0,
f(x)=a⋅(1b)x=a(b−1)x=a((en)−1)x=a(e−n)x=a(e)−nx
60) The formula for the amount A in an investment account with a nominal interest rate r at any time t is given by A(t)=a(e)rt, where a
Real-World Applications
61) The fox population in a certain region has an annual growth rate of 9% per year. In the year 2012, there were 23,900 fox counted in the area. What is the fox population predicted to be in the year 2020?
- Answer:
-
47,622 fox
62) A scientist begins with 100 milligrams of a radioactive substance that decays exponentially. After 35 hours, 50mg of the substance remains. How many milligrams will remain after 54 hours?
63) In the year 1985, a house was valued at $110,000. By the year 2005, the value had appreciated to $145,000. What was the annual growth rate between 1985 and 2005? Assume that the value continued to grow by the same percentage. What was the value of the house in the year 2010?
- Answer:
-
1.39%; $155,368.09
64) A car was valued at $38,000 in the year 2007. By 2013, the value had depreciated to $11,000 If the car’s value continues to drop by the same percentage, what will it be worth by 2017?
65) Jamal wants to save $54,000 for a down payment on a home. How much will he need to invest in an account with 8.2% APR, compounding daily, in order to reach his goal in 5 years?
- Answer:
-
$35,838.76
66) Kyoko has $10,000 that she wants to invest. Her bank has several investment accounts to choose from, all compounding daily. Her goal is to have $15,000 by the time she finishes graduate school in 6 years. To the nearest hundredth of a percent, what should her minimum annual interest rate be in order to reach her goal? (Hint: solve the compound interest formula for the interest rate.)
67) Alyssa opened a retirement account with 7.25% APR in the year 2000. Her initial deposit was $13,500. How much will the account be worth in 2025 if interest compounds monthly? How much more would she make if interest compounded continuously?
- Answer:
-
$82,247.78; $449.75
68) An investment account with an annual interest rate of 7% was opened with an initial deposit of $4,000 Compare the values of the account after 9 years when the interest is compounded annually, quarterly, monthly, and continuously.
4.2: Graphs of Exponential Functions
As we discussed in the previous section, exponential functions are used for many real-world applications such as finance, forensics, computer science, and most of the life sciences. Working with an equation that describes a real-world situation gives us a method for making predictions. Most of the time, however, the equation itself is not enough. We learn a lot about things by seeing their pictorial representations, and that is exactly why graphing exponential equations is a powerful tool.
Verbal
1) What role does the horizontal asymptote of an exponential function play in telling us about the end behavior of the graph?
- Answer:
-
An asymptote is a line that the graph of a function approaches, as x either increases or decreases without bound. The horizontal asymptote of an exponential function tells us the limit of the function’s values as the independent variable gets either extremely large or extremely small.
2) What is the advantage of knowing how to recognize transformations of the graph of a parent function algebraically?
Algebraic
3) The graph of f(x)=3x
- Answer:
-
g(x)=4(3)−x
; y-intercept: ;
4) The graph of f(x)=(12)−x
5) The graph of f(x)=10x is reflected about the x-axis and shifted upward 7 units. What is the equation of the new function, g(x)?
- Answer:
-
g(x)=−10x+7; y-intercept: (0,6); Domain: all real numbers; Range: all real numbers less than 7.
6) The graph of f(x)=(1.68)x is shifted right 3 units, stretched vertically by a factor of 2
7) The graph of f(x)=2(14)x−20 is shifted left 2 units, stretched vertically by a factor of 4
- Answer:
-
g(x)=2(14)x; y-intercept: (0,2);
Graphical
For the following exercises, graph the function and its reflection about the y-axis on the same axes, and give the y-intercept.
8) f(x)=3(12)x
9) g(x)=−2(0.25)x
- Answer:
-
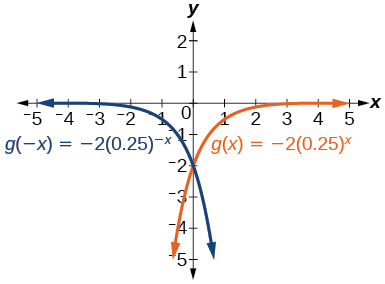
y-intercept: (0,−2)
10) h(x)=6(1.75)−x
For the following exercises, graph each set of functions on the same axes.
11) f(x)=3(14)x,g(x)=3(2)x,h(x)=3(4)x
- Answer:
-
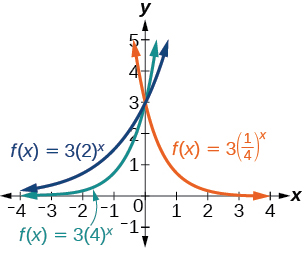
12) f(x)=14(3)x,g(x)=2(3)x,h(x)=4(3)x
For the following exercises, match each function with one of the graphs in Figure below.
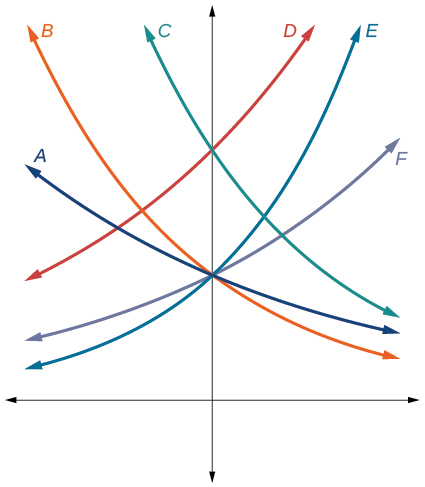
13) f(x)=2(0.69)x
- Answer:
-
B
14) f(x)=2(1.28)x
15) f(x)=2(0.81)x
- Answer:
-
A
16) f(x)=4(1.28)x
17) f(x)=2(1.59)x
- Answer:
-
E
18) f(x)=4(0.69)x
For the following exercises, use the graphs shown in Figure below. All have the form f(x)=abx.
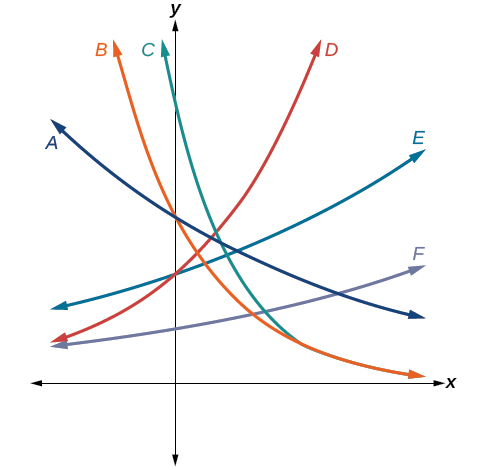
19) Which graph has the largest value for b?
- Answer:
-
D
20) Which graph has the smallest value for b?
21) Which graph has the largest value for a?
- Answer:
-
C
22) Which graph has the smallest value for a?
For the following exercises, graph the function and its reflection about the x-axis on the same axes.
23) f(x)=12(4)x
- Answer:
-
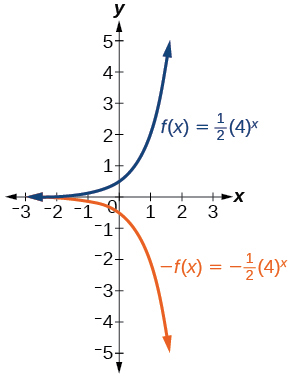
24) f(x)=3(0.75)x−1
25) f(x)=−4(2)x+2
- Answer:
-
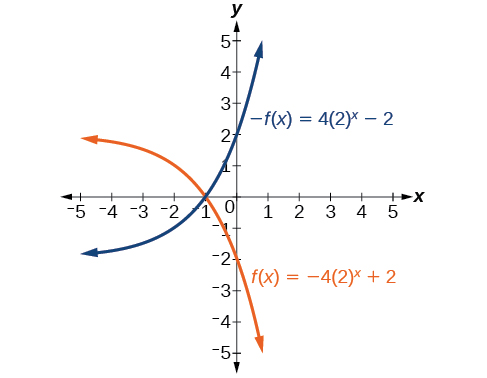
For the following exercises, graph the transformation of f(x)=2x
26) f(x)=2−x
27) h(x)=2x+3
- Answer:
-
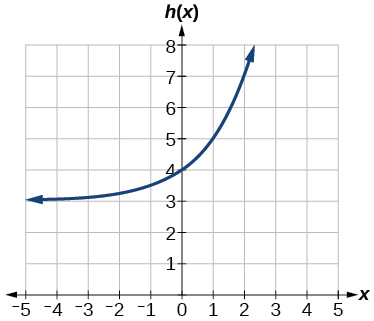
Horizontal asymptote: h(x)=3
;
28) f(x)=2x−2
For the following exercises, describe the end behavior of the graphs of the functions.
29) f(x)=−5(4)x−1
- Answer:
-
As x→∞,f(x)→−∞
As x→−∞,f(x)→−1
30) f(x)=3(12)x−2
31) f(x)=3(4)−x+2
- Answer:
-
As x→∞,f(x)→2
As x→−∞,f(x)→∞
For the following exercises, start with the graph of f(x)=4x
32) Shift f(x) 4 units upward
33) Shift f(x) 3 units downward
- Answer:
-
f(x)=4x−3
34) Shift f(x) 2 units left
35) Shift f(x) 5 units right
- Answer:
-
f(x)=4x−5
36) Reflect f(x) about the x-axis
37) Reflect f(x) about the y-axis
- Answer:
-
f(x)=4−x
For the following exercises, each graph is a transformation of f(x)=2x
38)
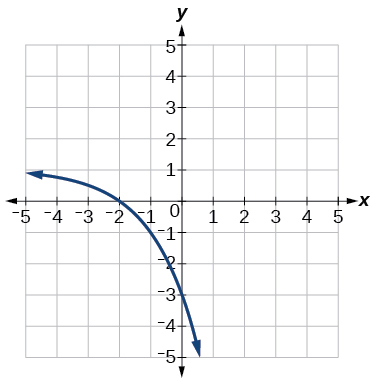
39)
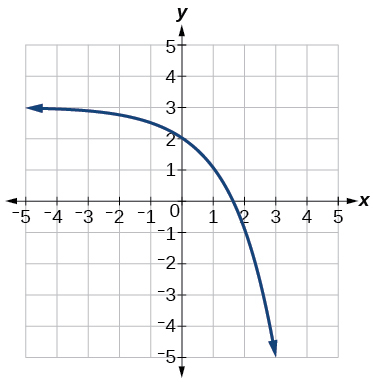
- Answer:
-
y=−2x+3
40)
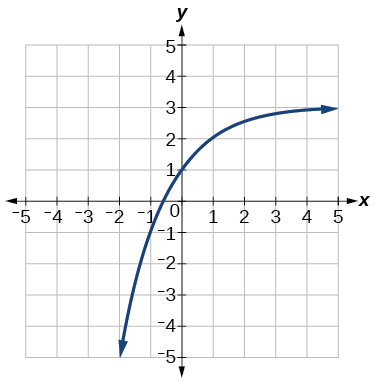
For the following exercises, find an exponential equation for the graph.
41)
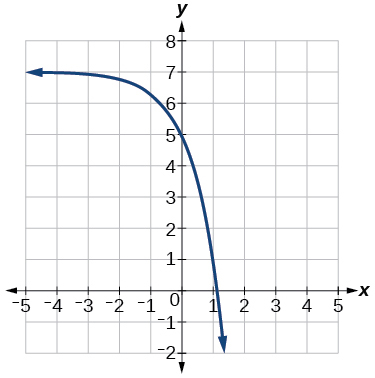
- Answer:
-
y=−2(3)x+7
42)
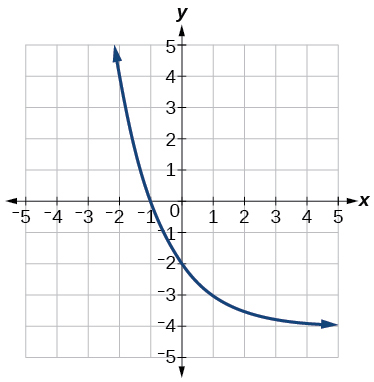
Numeric
For the following exercises, evaluate the exponential functions for the indicated value of x.
43) g(x)=13(7)x−2 for g(6).
- Answer:
-
g(6)=800+13≈800.3333
44) f(x)=4(2)x−1−2 for f(5).
45) h(x)=−12(12)x+6 for h(−7).
- Answer:
-
h(−7)=−58
Technology
For the following exercises, use a graphing calculator to approximate the solutions of the equation. Round to the nearest thousandth.
46) −50=(12)−x
47) 116=(14)(18)x
- Answer:
-
x≈−2.953
48) 12=2(3)x+1
49) 5=3(12)x−1−2
- Answer:
-
x≈−0.222
50) −30=−4(2)x+2+2
Extensions
51) Explore and discuss the graphs of F(x)=(b)x and G(x)=(1b)x. Then make a conjecture about the relationship between the graphs of the functions bx and (1b)x for any real number b>0.
- Answer:
-
The graph of G(x)=(1b)x is the refelction about the y-axis of the graph of F(x)=(b)x; For any real number b>0 and function f(x)=(b)x
,
52) Prove the conjecture made in the previous exercise.
53) Explore and discuss the graphs of f(x)=4x, g(x)=4x−2, and h(x)=(116)4x
- Answer:
-
The graphs of g(x) and h(x) are the same and are a horizontal shift to the right of the graph of f(x); For any real number n, real number b>0, and function f(x)=bx
,
54) Prove the conjecture made in the previous exercise.
4.3: Logarithmic Functions
The inverse of an exponential function is a logarithmic function, and the inverse of a logarithmic function is an exponential function.
Verbal
1) What is a base b logarithm? Discuss the meaning by interpreting each part of the equivalent equations by=x and logbx=y for b>0,b≠1.
- Answer
-
A logarithm is an exponent. Specifically, it is the exponent to which a base b is raised to produce a given value. In the expressions given, the base b has the same value. The exponent, y
, ,
2) How is the logarithmic function f(x)=logbx related to the exponential function g(x)=bx? What is the result of composing these two functions?
3) How can the logarithmic equation logbx=y be solved for x using the properties of exponents?
- Answer
-
Since the equation of a logarithm is equivalent to an exponential equation, the logarithm can be converted to the exponential equation by=x
, .
4) Discuss the meaning of the common logarithm. What is its relationship to a logarithm with base b
5) Discuss the meaning of the natural logarithm. What is its relationship to a logarithm with base b
- Answer
-
The natural logarithm is a special case of the logarithm with base b in that the natural log always has base e.
, .
Algebraic
For the following exercises, rewrite each equation in exponential form.
6) log4(q)=m
7) loga(b)=c
- Answer
-
ac=b
8) log16(y)=x
9) logx(64)=y
- Answer
-
xy=64
10) logy(x)=−11
11) log15(a)=b
- Answer
-
15b=a
12) logy(137)=x
13) log13(142)=a
- Answer
-
13a=142
14) log(v)=t
15) ln(w)=n
- Answer
-
en=w
For the following exercises, rewrite each equation in logarithmic form.
16) 4x=y
17) cd=k
- Answer
-
logc(k)=d
18) m−7=n
19) 19x=y
- Answer
-
log19(y)=x
20) x−1013=y
21) n4=103
- Answer
-
logn(103)=4
22) (75)m=n
23) yx=39100
- Answer
-
logy(39100)=x
24) 10a=b
25) ek=h
- Answer
-
ln(w)=n
For the following exercises, solve for x by converting the logarithmic equation to exponential form.
26) log3(x)=2
27) log2(x)=−3
- Answer
-
x=2−3=18
28) log5(x)=2
29) log3(x)=3
- Answer
-
x=33=27
30) log2(x)=6
31) log9(x)=12
- Answer
-
x=912=3
32) log18(x)=2
33) log6(x)=−3
- Answer
-
x=6−3=1216
34) log(x)=3
35) ln(x)=2
- Answer
-
x=e2
For the following exercises, use the definition of common and natural logarithms to simplify.
36) log(1008)
37) 10log(32)
- Answer
-
32
38) 2log(.0001)
39) eln(1.06)
- Answer
-
1.06
40) ln(e−5.03)
41) eln(10.125)+4
- Answer
-
14.125
Numeric
For the following exercises, evaluate the base b logarithmic expression without using a calculator.
42) log3(127)
43) log6(√6)
- Answer
-
12
44) log2(18)+4
45) 6log8(4)
- Answer
-
4
For the following exercises, evaluate the common logarithmic expression without using a calculator.
46) log(10,000)
47) log(0.001)
- Answer
-
−3
48) log(1)+7
49) 2log(100−3)
- Answer
-
−12
For the following exercises, evaluate the natural logarithmic expression without using a calculator.
50) ln(e13)
51) ln(1)
- Answer
-
0
52) ln(e−0.225)−3
53) 25ln(e25)
- Answer
-
10
Technology
For the following exercises, evaluate each expression using a calculator. Round to the nearest thousandth.
54) log(0.04)
55) ln(15)
- Answer
-
2.708
56) ln(45)
57) log(√2)
- Answer
-
0.151
58) ln(√2)
Extensions
59) Is x=0 in the domain of the function f(x)=logx? If so, what is the value of the function when x=0? Verify the result.
- Answer
-
No, the function has no defined value for x=0
. . . ,
60) Is f(x)=0 in the range of the function f(x)=log(x)?
61) Is there a number x such that lnx=2? If so, what is that number? Verify the result.
- Answer
-
Yes. Suppose there exists a real number x such that lnx=2
. , . .
62) Is the following true: log3(27)log4(164)=−1
63) Is the following true: ln(e1.725)ln(1)=1.725 Verify the result.
- Answer
-
No; ln(1)=0, so ln(e1.725)ln(1)=1.725 is undefined.
Real-World Applications
64) The exposure index EI for a 35 millimeter camera is a measurement of the amount of light that hits the film. It is determined by the equation EI=log2(f2t)
65) Refer to the previous exercise. Suppose the light meter on a camera indicates an EI of −2
- Answer
-
2
66) The intensity levels I of two earthquakes measured on a seismograph can be compared by the formula log(I1I2)=M1−M2
4.4: Graphs of Logarithmic Functions
In this section we will discuss the values for which a logarithmic function is defined, and then turn our attention to graphing the family of logarithmic functions.
Verbal
1) The inverse of every logarithmic function is an exponential function and vice-versa. What does this tell us about the relationship between the coordinates of the points on the graphs of each?
- Answer
-
Since the functions are inverses, their graphs are mirror images about the line y−x
.
2) What type(s) of translation(s), if any, affect the range of a logarithmic function?
3) What type(s) of translation(s), if any, affect the domain of a logarithmic function?
- Answer
-
Shifting the function right or left and reflecting the function about the y-axis will affect its domain.
4) Consider the general logarithmic function f(x)=logb(x)
5) Does the graph of a general logarithmic function have a horizontal asymptote? Explain.
- Answer
-
No. A horizontal asymptote would suggest a limit on the range, and the range of any logarithmic function in general form is all real numbers.
Algebraic
For the following exercises, state the domain and range of the function.
6) f(x)=log3(x+4)
7) h(x)=ln(12−x)
- Answer
-
Domain: (−∞,12); Range: (−∞,∞)
8) g(x)=log5(2x+9)−2
9) h(x)=ln(4x+17)−5
- Answer
-
Domain: (−174,∞); Range: (−∞,∞)
10) f(x)=log2(12−3x)−3
For the following exercises, state the domain and the vertical asymptote of the function.
11) f(x)=logb(x−5)
- Answer
-
Domain: (5,∞); Vertical asymptote: x=5
12) g(x)=ln(3−x)
13) f(x)=log(3x+1)
- Answer
-
Domain: (−13,∞); Vertical asymptote: x=−13
14) f(x)=3log(−x)+2
15) g(x)=−ln(3x+9)−7
- Answer
-
Domain: (−3,∞); Vertical asymptote: x=−3
For the following exercises, state the domain, vertical asymptote, and end behavior of the function.
16) f(x)=ln(2−x)
17) f(x)=log(x−37)
- Answer
-
Domain: (37,∞)
Vertical asymptote: x=37
End behavior: as x→(37)+, f(x)→−∞ and as x→∞,f(x)→∞
18) h(x)=−log(3x−4)+3
19) g(x)=ln(2x+6)−5
- Answer
-
Domain: (−3,∞)
Vertical asymptote: x=−3
End behavior: as x→−3+, f(x)→−∞ and as x→∞,f(x)→∞
20) f(x)=log3(15−5x)+6
For the following exercises, state the domain, range, and x- and y-intercepts, if they exist. If they do not exist, write DNE.
21) h(x)=log4(x−1)+1
- Answer
-
Domain: (1,∞)
Range: −∞,∞
Vertical asymptote: x=1
x-intercept: (54,0)
y-intercept: DNE
22) f(x)=log(5x+10)+3
23) g(x)=ln(−x)−2
- Answer
-
Domain: (−∞,0)
Range: −∞,∞
Vertical asymptote: x=0
x-intercept: (−e2,0)
y-intercept: DNE
24) f(x)=log2(x+2)−5
25) h(x)=3ln(x)−9
- Answer
-
Domain: (0,∞)
Range: −∞,∞
Vertical asymptote: x=0
x-intercept: (e3,0)
y-intercept: DNE
Graphical
For the following exercises, match each function in Figure below with the letter corresponding to its graph.
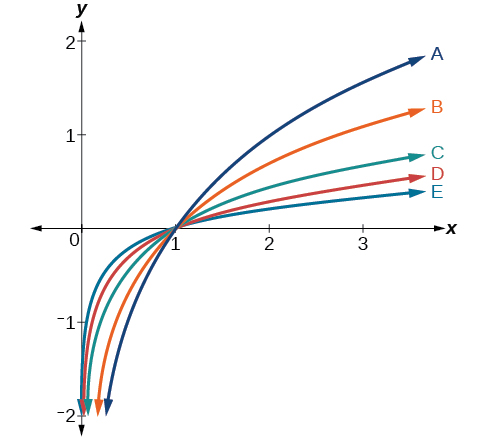
26) d(x)=log(x)
27) f(x)=ln(x)
- Answer
-
B
28) g(x)=log2(x)
29) h(x)=log5(x)
- Answer
-
C
30) j(x)=log25(x)
For the following exercises, match each function in Figure with the letter corresponding to its graph.
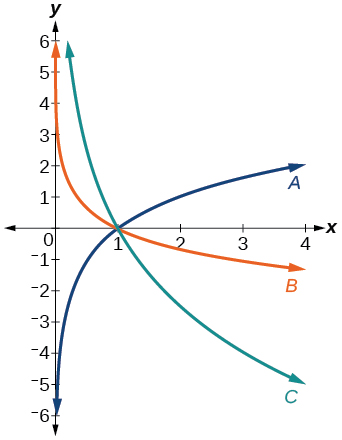
31) f(x)=log13(x)
- Answer
-
B
32) g(x)=log2(x)
33) h(x)=log34(x)
- Answer
-
C
For the following exercises, sketch the graphs of each pair of functions on the same axis.
34) f(x)=log(x) and g(x)=10x
35) f(x)=ex and g(x)=ln(x)
- Answer
-
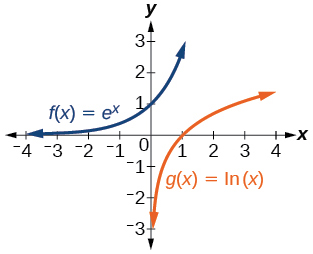
For the following exercises, match each function in Figure with the letter corresponding to its graph.
36) f(x)=log4(−x+2)
37) g(x)=−log4(x+2)
- Answer
-
C
38) h(x)=log4(x+2)
For the following exercises, sketch the graph of the indicated function.
39) f(x)=log2(x+2)
- Answer
-
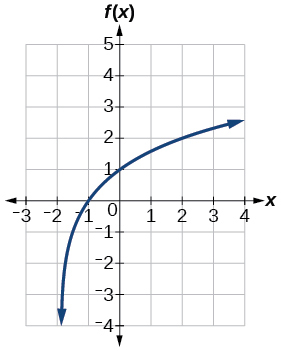
40) f(x)=2log(x)
41) f(x)=ln(−x)
- Answer
-
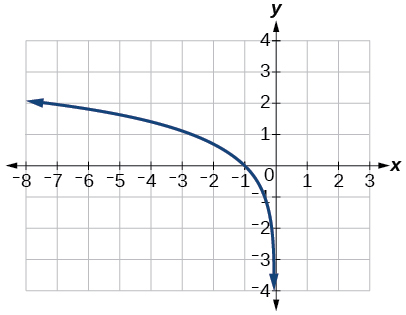
42) g(x)=log(4x+16)+4
43) g(x)=log(6−3x)+1
- Answer
-
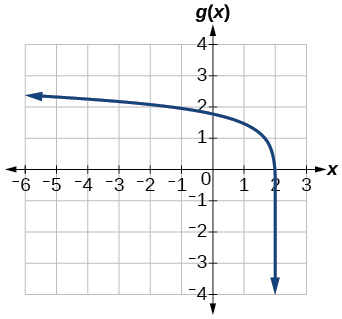
44) h(x)=−12log(x+1)−3
For the following exercises, write a logarithmic equation corresponding to the graph shown.
45) Use y=log2(x)

- Answer
-
f(x)=log2(−(x−1))
46) Use f(x)=log3(x) as the parent function.
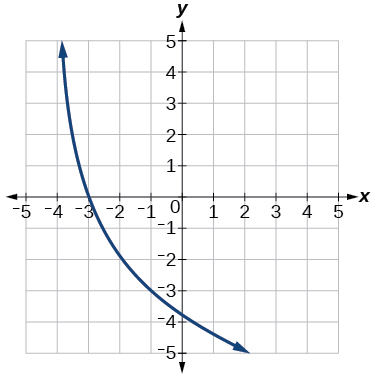
47) Use f(x)=log4(x) as the parent function.
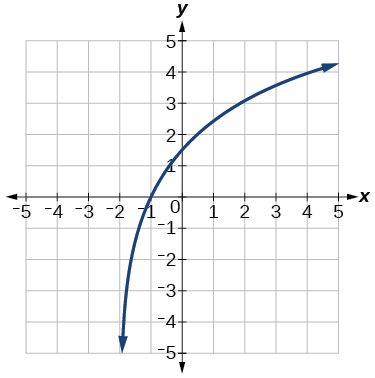
- Answer
-
f(x)=3log4(x+2)
48) Use f(x)=log5(x) as the parent function.
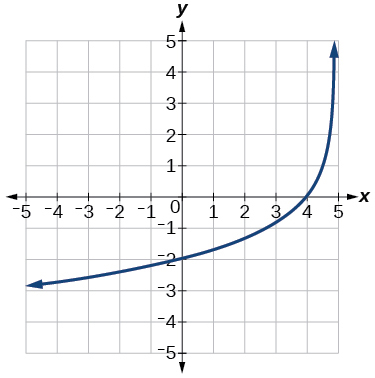
Technology
For the following exercises, use a graphing calculator to find approximate solutions to each equation.
49) log(x−1)+2=ln(x−1)+2
- Answer
-
x=2
50) log(2x−3)+2=−log(2x−3)+5
51) ln(x−2)+2=−ln(x+1)
- Answer
-
x≈2.303
52) 2ln(5x+1)=12ln(−5x)+1
53) 13log(1−x)=log(x+1)+13
- Answer
-
x≈−0.472
Extensions
54) Let b be any positive real number such that b≠1
55) Explore and discuss the graphs of f(x)=log12(x) and g(x)=−log2(x)
- Answer
-
The graphs of f(x)=log12(x) and g(x)=−log2(x) appear to be the same;
Conjecture: for any positive base b≠1, logb(x)=log1b(x)
56) Prove the conjecture made in the previous exercise.
57) What is the domain of the function f(x)=ln(x+2x−4)
- Answer
-
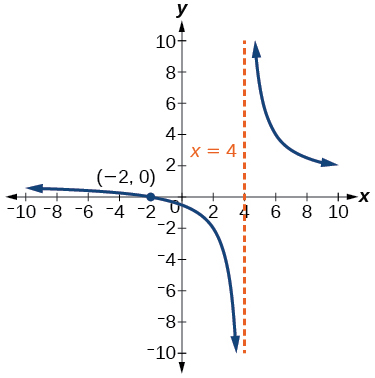
Recall that the argument of a logarithmic function must be positive, so we determine where x+2x−4>0. From the graph of the function f(x)=x+2x−4
, . . 
58) Use properties of exponents to find the x-intercepts of the function f(x)=log(x2+4x+4) algebraically. Show the steps for solving, and then verify the result by graphing the function.
4.5: Logarithmic Properties
Recall that the logarithmic and exponential functions “undo” each other. This means that logarithms have similar properties to exponents. Some important properties of logarithms are given here.
Verbal
1) How does the power rule for logarithms help when solving logarithms with the form logb(n√x)
- Answer
-
Any root expression can be rewritten as an expression with a rational exponent so that the power rule can be applied, making the logarithm easier to calculate. Thus, logb(x1n)=1nlogb(x).
2) What does the change-of-base formula do? Why is it useful when using a calculator?
Algebraic
For the following exercises, expand each logarithm as much as possible. Rewrite each expression as a sum, difference, or product of logs.
3) logb(7x⋅2y)
- Answer
-
logb(2)+logb(7)+logb(x)+logb(y)
4) ln(3ab⋅5c)
5) logb(1317)
- Answer
-
logb(13)−logb(17)
6) log4(xzw)
7) ln(14k)
- Answer
-
−kln(4)
8) log2(yx)
For the following exercises, condense to a single logarithm if possible.
9) ln(7)+ln(x)+ln(y)
- Answer
-
ln(7xy)
10) log3(2)+log3(a)+log3(11)+log3(b)
11) logb(28)−logb(7)
- Answer
-
logb(4)
12) ln(a)−ln(d)−ln(c)
13) −logb(17)
- Answer
-
logb(7)
14) 13ln(8)
For the following exercises, use the properties of logarithms to expand each logarithm as much as possible. Rewrite each expression as a sum, difference, or product of logs.
15) log(x15y13z19)
- Answer
-
15log(x)+13log(y)−19log(z)
16) ln(a−2b−4c5)
17) log(√x3y−4)
- Answer
-
32log(x)−2log(y)
18) ln(y√y1−y)
19) log(x2y33√x2y5)
- Answer
-
83log(x)+143log(y)
For the following exercises, condense each expression to a single logarithm using the properties of logarithms.
20) log(2x4)+log(3x5)
21) ln(6x9)−ln(3x2)
- Answer
-
ln(2x7)
22) 2log(x)+3log(x+1)
23) log(x)−12log(y)+3log(z)
- Answer
-
log(xz3√y)
24) 4log7(c)+log7(a)3+log7(b)3
For the following exercises, rewrite each expression as an equivalent ratio of logs using the indicated base.
25) log7(15) to base e
- Answer
-
log7(15)=ln(15)ln(7)
For the following exercises, suppose log5(6)=a and log5(11)=b
27) log11(5)
- Answer
-
log11(5)=log5(5)log5(11)=1b
28) log6(55)
29) log11(611)
- Answer
-
log11(611)=log11(611)log5(11)=log5(6)−log5(11)log5(11)=a−bb=ab−1
Numeric
For the following exercises, use properties of logarithms to evaluate without using a calculator.
30) log3(19)−3log3(3)
31) 6log8(2)+log8(64)3log8(4)
- Answer
-
3
32) 2log9(3)−4log9(3)+log9(1729)
For the following exercises, use the change-of-base formula to evaluate each expression as a quotient of natural logs. Use a calculator to approximate each to five decimal places.
33) log3(22)
- Answer
-
2.81359
34) log8(65)
35) log6(5.38)
- Answer
-
0.93913
36) log4(152)
37) log12(4.7)
- Answer
-
−2.23266
Extensions
38) Use the product rule for logarithms to find all x values such that log12(2x+6)+log12(x+2)=2
39) Use the quotient rule for logarithms to find all x values such that log6(x+2)−log6(x−3)=1
- Answer
-
Rewriting as an exponential equation and solving for x:
61=x+2x−30=x+2x−3−60=x+2x−3−6(x−3)(x−3)0=x+2−6x+18x−30=x−4x−3x=4
Checking, we find that log6(4+2)−log6(4−3)=log6(6)−log6(1) is defined, so x=4
40) Can the power property of logarithms be derived from the power property of exponents using the equation bx=m
41) Prove that logb(n)=1logb(n) for any positive integers b>1 and n>1
- Answer
-
Let b and n be positive integers greater than 1
.
42) Does log81(2401)=log3(7)
4.6: Exponential and Logarithmic Equations
Uncontrolled population growth can be modeled with exponential functions. Equations resulting from those exponential functions can be solved to analyze and make predictions about exponential growth. In this section, we will learn techniques for solving exponential functions.
Verbal
1) How can an exponential equation be solved?
- Answer
-
Determine first if the equation can be rewritten so that each side uses the same base. If so, the exponents can be set equal to each other. If the equation cannot be rewritten so that each side uses the same base, then apply the logarithm to each side and use properties of logarithms to solve.
2) When does an extraneous solution occur? How can an extraneous solution be recognized?
3) When can the one-to-one property of logarithms be used to solve an equation? When can it not be used?
- Answer
-
The one-to-one property can be used if both sides of the equation can be rewritten as a single logarithm with the same base. If so, the arguments can be set equal to each other, and the resulting equation can be solved algebraically. The one-to-one property cannot be used when each side of the equation cannot be rewritten as a single logarithm with the same base.
Algebraic
For the following exercises, use like bases to solve the exponential equation.
4) 4−3v−2=4−v
5) 64⋅43x=16
- Answer
-
x=−13
6) 32x+1⋅3x=243
7) 2−3n⋅14=2n+2
- Answer
-
n=−1
8) 625⋅53x+3=125
9) 363b362b=2162−b
- Answer
-
b=65
10) (164)3n⋅8=26
For the following exercises, use logarithms to solve.
11) 9x−10=1
- Answer
-
x=10
12) 2e6x=13
13) er+10−10=−42
- Answer
-
No solution
14) 2⋅109a=29
15) −8⋅10p+7−7=−24
- Answer
-
p=log(178)−7
16) 7e3n−5+5=−89
17) e−3k+6=44
- Answer
-
k=−ln(38)3
18) −5e9x−8−8=−62
19) −6e9x+8+2=−74
- Answer
-
x=ln(38)3−89
20) 2x+1=52x−1
21) e2x−ex−132=0
- Answer
-
x=ln12
22) 7e8x+8−5=−95
23) 10e8x+3+2=8
- Answer
-
x=ln(3)5−38
24) 4e3x+3−7=53
25) 8e−5x−2−4=−90
- Answer
-
No solution
26) 32x+1=7x−2
27) e2x−ex−6=0
- Answer
-
x=ln3
28) 3e3−3x+6=−31
For the following exercises, use the definition of a logarithm to rewrite the equation as an exponential equation.
29) log(1100)=−2
- Answer
-
10−2=1100
30) log324(18)=12
For the following exercises, use the definition of a logarithm to solve the equation.
31) 5log7n=10
- Answer
-
n=49
32) −8log9x=16
33) 4+log2(9k)=2
- Answer
-
k=136
34) 2log(8n+4)+6=10
35) 10−4ln(9−8x)=6
- Answer
-
x=9−e8
For the following exercises, use the one-to-one property of logarithms to solve.
36) ln(10−3x)=ln(−4x)
37) log13(5n−2)=log13(8−5n)
- Answer
-
n=1
38) log(x+3)−log(x)=log(74)
39) ln(−3x)=ln(x2−6x)
- Answer
-
No solution
40) log4(6−m)=log4(3m)
41) ln(x−2)−ln(x)=ln(54)
- Answer
-
No solution
42) log9(2n2−14n)=log9(−45+n2)
43) ln(x2−10)+ln(9)=ln(10)
- Answer
-
x=±103
For the following exercises, solve each equation for x.
44) log(x+12)=log(x)+log(12)
45) ln(x)+ln(x−3)=ln(7x)
- Answer
-
x=10
46) log2(7x+6)=3
47) ln(7)+ln(2−4x2)=ln(14)
- Answer
-
x=0
48) log8(x+6)−log8(x)=log8(58)
49) ln(3)−ln(3−3x)=ln(4)
- Answer
-
x=34
50) log3(3x)−log3(6)=log3(77)
Graphical
For the following exercises, solve the equation for x
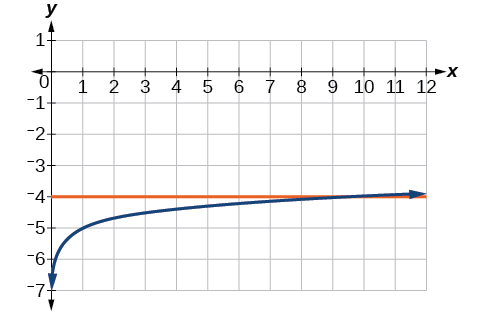
51) log9(x)−5=−4
- Answer
-
x=9
52) log3(x)+3=2
53) ln(3x)=2
- Answer
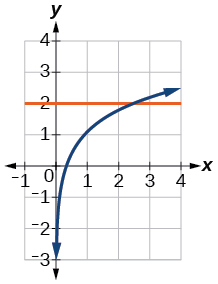
-
x=e23≈2.5
54) ln(x−5)=1
55) log(4)+log(−5x)=2
- Answer
-
x=−5
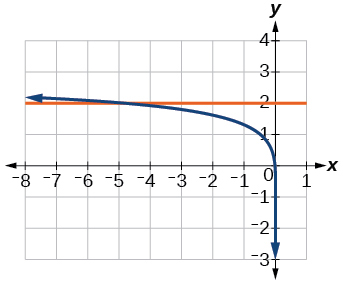
56) −7+log3(4−x)=−6
57) ln(4x−10)−6=−5
- Answer
-
x=e+104≈3.2
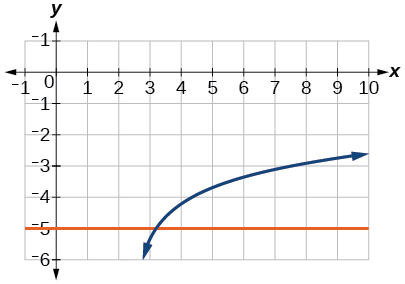
58) log(4−2x)=log(−4x)
59) log11(−2x2−7x)=log11(x−2)
- Answer
-
No solution
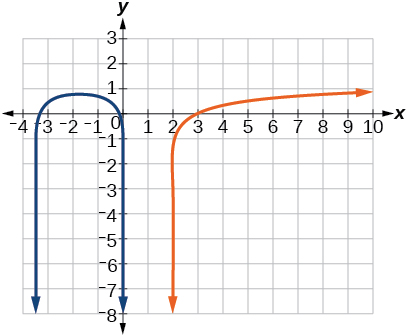
60) ln(2x+9)=ln(−5x)
61) log9(3−x)=log9(4x−8)
- Answer
-
x=115≈2.2
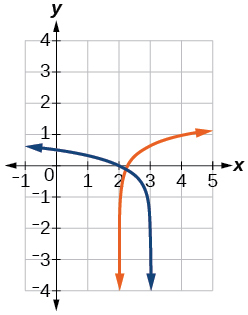
62) log(x2+13)=log(7x+3)
63) 3log2(10)−log(x−9)=log(44)
- Answer
-
x=10111≈9.2
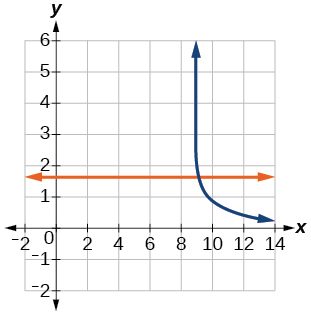
64) ln(x)−ln(x+3)=ln(6)
For the following exercises, solve for the indicated value, and graph the situation showing the solution point.
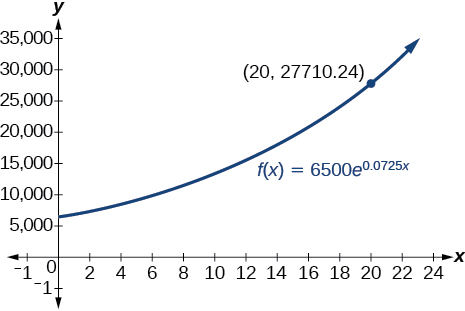
65) An account with an initial deposit of $6,500 earns 7.25% annual interest, compounded continuously. How much will the account be worth after 20 years?
- Answer
-
about $27,710.24
66) The formula for measuring sound intensity in decibels D is defined by the equation D=10log(II0)
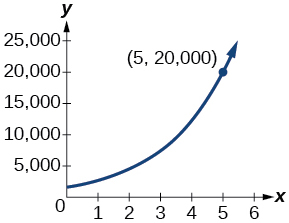
67) The population of a small town is modeled by the equation P=1650e0.5t where t is measured in years. In approximately how many years will the town’s population reach 20,000?
- Answer
-
about 5 years
Technology
For the following exercises, solve each equation by rewriting the exponential expression using the indicated logarithm. Then use a calculator to approximate the variable to 3 decimal places.
68) 1000(1.03)t=5000 using the common log.
69) e5x=17 using the natural log.
- Answer
-
ln(17)5≈0.567
70) 3(1.04)3t=8 using the common log
71) 34x−5=38 using the common log
- Answer
-
x=log(38+5log(3))4log(3)≈2.078
72) 50e−0.12t=10 using the natural log
For the following exercises, use a calculator to solve the equation. Unless indicated otherwise, round all answers to the nearest ten-thousandth.
73) 7e3x−5+7.9=47
- Answer
-
x≈2.2401
74) ln(3)+ln(4.4x+6.8)=2
75) log(−0.7x−9)=1+5log(5)
- Answer
-
x≈−44655.7143
76) Atmospheric pressure P in pounds per square inch is represented by the formula P=14.7e−0.21x
77) The magnitude M of an earthquake is represented by the equation M=23log(EE0) where E is the amount of energy released by the earthquake in joules E0=104.4 and is the assigned minimal measure released by an earthquake. To the nearest hundredth, what would the magnitude be of an earthquake releasing 1.4⋅1013 joules of energy?
- Answer
-
about 5.83
Extensions
78) Use the definition of a logarithm along with the one-to-one property of logarithms to prove that blogbx=x.
79) Recall the formula for continually compounding interest, y=Aekt
- Answer
-
t=ln((yA)1k)
80) Recall the compound interest formula A=a(1+rk)kt
81) Newton’s Law of Cooling states that the temperature T of an object at any time t can be described by the equation T=Ts+(T0−Ts)e−kt
- Answer
-
t=ln((T−TsT0−Ts)−1k)
4.7: Exponential and Logarithmic Models
We have already explored some basic applications of exponential and logarithmic functions. In this section, we explore some important applications in more depth, including radioactive isotopes and Newton’s Law of Cooling.
Verbal
1) With what kind of exponential model would half-life be associated? What role does half-life play in these models?
- Answer
-
Half-life is a measure of decay and is thus associated with exponential decay models. The half-life of a substance or quantity is the amount of time it takes for half of the initial amount of that substance or quantity to decay.
2) What is carbon dating? Why does it work? Give an example in which carbon dating would be useful.
3) With what kind of exponential model would doubling time be associated? What role does doubling time play in these models?
- Answer
-
Doubling time is a measure of growth and is thus associated with exponential growth models. The doubling time of a substance or quantity is the amount of time it takes for the initial amount of that substance or quantity to double in size.
4) Define Newton’s Law of Cooling. Then name at least three real-world situations where Newton’s Law of Cooling would be applied.
5) What is an order of magnitude? Why are orders of magnitude useful? Give an example to explain.
- Answer
-
An order of magnitude is the nearest power of ten by which a quantity exponentially grows. It is also an approximate position on a logarithmic scale; Sample response: Orders of magnitude are useful when making comparisons between numbers that differ by a great amount. For example, the mass of Saturn is 95 times greater than the mass of Earth. This is the same as saying that the mass of Saturn is about 102 times, or 2 orders of magnitude greater, than the mass of Earth.
Numeric
6) The temperature of an object in degrees Fahrenheit after t minutes is represented by the equation T(t)=68e−0.0174t+72
For the following exercises, use the logistic growth model f(x)=1501+8e−2x
7) Find and interpret f(0)
- Answer
-
f(0)≈16.7; The amount initially present is about 16.7 units.
8) Find and interpret f(4)
9) Find the carrying capacity.
- Answer
-
150
10) Graph the model.
11) Determine whether the data from the table could best be represented as a function that is linear, exponential, or logarithmic. Then write a formula for a model that represents the data.
| x | f(x) |
|---|---|
| –2 | 0.694 |
| –1 | 0.833 |
| 0 | 1 |
| 1 | 1.2 |
| 2 | 1.44 |
| 3 | 1.728 |
| 4 | 2.074 |
| 5 | 2.488 |
- Answer
-
exponential; f(x)=1.2x
12) Rewrite f(x)=1.68(0.65)x as an exponential equation with base e to five significant digits.
Technology
For the following exercises, enter the data from each table into a graphing calculator and graph the resulting scatter plots. Determine whether the data from the table could represent a function that is linear, exponential, or logarithmic.
13)
| x | f(x) |
|---|---|
| 1 | 2 |
| 2 | 4.079 |
| 3 | 5.296 |
| 4 | 6.159 |
| 5 | 6.828 |
| 6 | 7.375 |
| 7 | 7.838 |
| 8 | 8.238 |
| 9 | 8.592 |
| 10 | 8.908 |
- Answer
-
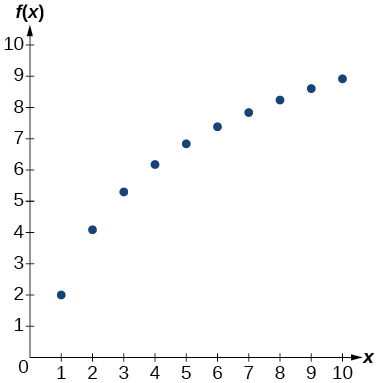
14)
| x | f(x) |
|---|---|
| 1 | 2.4 |
| 2 | 2.88 |
| 3 | 3.456 |
| 4 | 4.147 |
| 5 | 4.977 |
| 6 | 5.972 |
| 7 | 7.166 |
| 8 | 8.6 |
| 9 | 10.32 |
| 10 | 12.383 |
15)
| x | f(x) |
|---|---|
| 4 | 9.429 |
| 5 | 9.972 |
| 6 | 10.415 |
| 7 | 10.79 |
| 8 | 11.115 |
| 9 | 11.401 |
| 10 | 11.657 |
| 11 | 11.889 |
| 12 | 12.101 |
| 13 | 12.295 |
- Answer
-
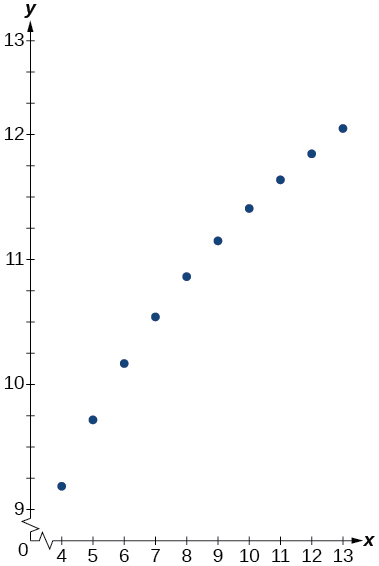
16)
| x | f(x) |
|---|---|
| 1.25 | 5.75 |
| 2.25 | 8.75 |
| 3.56 | 12.68 |
| 4.2 | 14.6 |
| 5.65 | 18.95 |
| 6.75 | 22.25 |
| 7.25 | 23.75 |
| 8.6 | 27.8 |
| 9.25 | 29.75 |
| 10.5 | 33.5 |
For the following exercises, use a graphing calculator and this scenario: the population of a fish farm in t years is modeled by the equation P(t)=10001+9e−0.6t
17) Graph the function.
- Answer
-
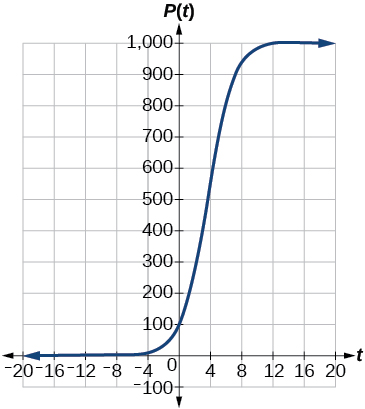
18) What is the initial population of fish?
19) To the nearest tenth, what is the doubling time for the fish population?
- Answer
-
about 1.4 years
20) To the nearest whole number, what will the fish population be after 2 years?
21) To the nearest tenth, how long will it take for the population to reach 900?
- Answer
-
about 7.3 years
22) What is the carrying capacity for the fish population? Justify your answer using the graph of P.
Extensions
23) A substance has a half-life of 2.045 minutes. If the initial amount of the substance was 132.8 grams, how many half-lives will have passed before the substance decays to 8.3 grams? What is the total time of decay?
- Answer
-
4 half-lives; 8.18 minutes
24) The formula for an increasing population is given by P(t)=P0ert where P0 is the initial population and r>0
25) Recall the formula for calculating the magnitude of an earthquake, M=23log(SS0)
- Answer
-
M=23log(SS0)log(SS0)=32MSS0=103M2S=S0103M2
26) What is the y-intercept of the logistic growth model y=c1+ae−rx
27) Prove that bx=exln(b) for positive b≠1.
- Answer
-
Let y=bx for some non-negative real number b such that b≠1
. ln(y)=ln(bx)ln(y)=xln(b)eln(y)=exln(b)y=exln(b)
Real-World Applications
For the following exercises, use this scenario: A doctor prescribes 125 milligrams of a therapeutic drug that decays by about 30% each hour.
28) To the nearest hour, what is the half-life of the drug?
29) Write an exponential model representing the amount of the drug remaining in the patient’s system after t hours. Then use the formula to find the amount of the drug that would remain in the patient’s system after 3 hours. Round to the nearest milligram.
- Answer
-
A=125e(−0.3567t); A≈43 mg
30) Using the model found in the previous exercise, find f(10 and interpret the result. Round to the nearest hundredth.
For the following exercises, use this scenario: A tumor is injected with 0.5 grams of Iodine-125, which has a decay rate of 1.15% per day.
31) To the nearest day, how long will it take for half of the Iodine-125 to decay?
- Answer
-
about 60 days
32) Write an exponential model representing the amount of Iodine-125 remaining in the tumor after t days. Then use the formula to find the amount of Iodine-125 that would remain in the tumor after 60 days. Round to the nearest tenth of a gram.
33) A scientist begins with 250 grams of a radioactive substance. After 250 minutes, the sample has decayed to 32 grams. Rounding to five significant digits, write an exponential equation representing this situation. To the nearest minute, what is the half-life of this substance?
- Answer
-
f(t)=250e(−0.00914t)
;
34) The half-life of Radium-226 is 1590 years. What is the annual decay rate? Express the decimal result to four significant digits and the percentage to two significant digits.
35) The half-life of Erbium-165 is 10.4 hours. What is the hourly decay rate? Express the decimal result to four significant digits and the percentage to two significant digits.
- Answer
-
r≈−0.0667
,
36) A wooden artifact from an archeological dig contains 60 percent of the carbon-14 that is present in living trees. To the nearest year, about how many years old is the artifact? (The half-life of carbon-14 is 5730 years.)
37) A research student is working with a culture of bacteria that doubles in size every twenty minutes. The initial population count was 1350 bacteria. Rounding to five significant digits, write an exponential equation representing this situation. To the nearest whole number, what is the population size after 3 hours?
- Answer
-
f(t)=1350e(0.03466t); after 3 hours: P(180)≈691,200
For the following exercises, use this scenario: A biologist recorded a count of 360 bacteria present in a culture after 5 minutes and 1000 bacteria present after 20 minutes.
38) To the nearest whole number, what was the initial population in the culture?
39) Rounding to six significant digits, write an exponential equation representing this situation. To the nearest minute, how long did it take the population to double?
- Answer
-
f(t)=256e(0.068110t); doubling time: about 10 minutes
For the following exercises, use this scenario: A pot of boiling soup with an internal temperature of 100∘ Fahrenheit was taken off the stove to cool in a 69∘ F room. After fifteen minutes, the internal temperature of the soup was 95∘ F.
40) Use Newton’s Law of Cooling to write a formula that models this situation.
41) To the nearest minute, how long will it take the soup to cool to 80∘ F?
- Answer
-
about 88 minutes
42) To the nearest degree, what will the temperature be after 2 and a half hours?
For the following exercises, use this scenario: A turkey is taken out of the oven with an internal temperature of 165∘ F and is allowed to cool in a 75∘ F room. After half an hour, the internal temperature of the turkey is 145∘ F.
43) Write a formula that models this situation.
- Answer
-
T(t)=90e(−0.008377t)+75, where t is in minutes.
44) To the nearest degree, what will the temperature be after 50 minutes?
45) To the nearest minute, how long will it take the turkey to cool to 110∘ F?
- Answer
-
about 113 minutes
For the following exercises, find the value of the number shown on each logarithmic scale. Round all answers to the nearest thousandth.

- Answer
-
log(x)=1.5;x≈31.623
48) Plot each set of approximate values of intensity of sounds on a logarithmic scale: Whisper: 10−10Wm2
49) Recall the formula for calculating the magnitude of an earthquake, M=\dfrac{2}{3}\log \left ( \dfrac{S}{S_0} \right )
- Answer
-
MMS magnitude: 5.82
For the following exercises, use this scenario: The equation N(t)=\dfrac{500}{1+49e^{-0.7t}} models the number of people in a town who have heard a rumor after t days.
50) How many people started the rumor?
51) To the nearest whole number, how many people will have heard the rumor after 3 days?
- Answer
-
N(3)\approx 71
52) As t
For the following exercise, choose the correct answer choice.
53) A doctor and injects a patient with 13 milligrams of radioactive dye that decays exponentially. After 12 minutes, there are 4.75 milligrams of dye remaining in the patient’s system. Which is an appropriate model for this situation?
- f(t)=13(0.0805)^t
- f(t)=13e^{0.9195t}
- f(t)=13e^{(-0.0839t)}
- f(t)=\frac{4.75}{1+13e^{-0.83925t}}
- Answer
-
c
4.8: Fitting Exponential Models to Data
We will concentrate on three types of regression models in this section: exponential, logarithmic, and logistic. Having already worked with each of these functions gives us an advantage. Knowing their formal definitions, the behavior of their graphs, and some of their real-world applications gives us the opportunity to deepen our understanding. As each regression model is presented, key features and definitions of its associated function are included for review.
Verbal
1) What situations are best modeled by a logistic equation? Give an example, and state a case for why the example is a good fit.
- Answer
-
Logistic models are best used for situations that have limited values. For example, populations cannot grow indefinitely since resources such as food, water, and space are limited, so a logistic model best describes populations.
2) What is a carrying capacity? What kind of model has a carrying capacity built into its formula? Why does this make sense?
3) What is regression analysis? Describe the process of performing regression analysis on a graphing utility.
- Answer
-
Regression analysis is the process of finding an equation that best fits a given set of data points. To perform a regression analysis on a graphing utility, first list the given points using the STAT then EDIT menu. Next graph the scatter plot using the STAT PLOT feature. The shape of the data points on the scatter graph can help determine which regression feature to use. Once this is determined, select the appropriate regression analysis command from the STAT then CALC menu.
4) What might a scatterplot of data points look like if it were best described by a logarithmic model?
5) What does the y-intercept on the graph of a logistic equation correspond to for a population modeled by that equation?
- Answer
-
The y-intercept on the graph of a logistic equation corresponds to the initial population for the population model.
Graphical
For the following exercises, match the given function of best fit with the appropriate scatterplot in Figure (a) through Figure (e). Answer using the letter beneath the matching graph.
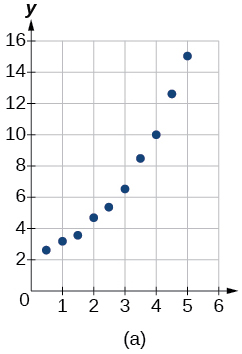
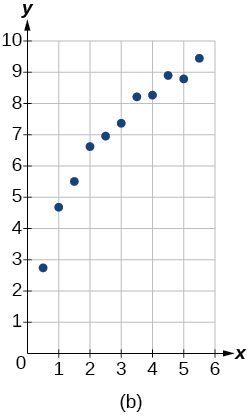
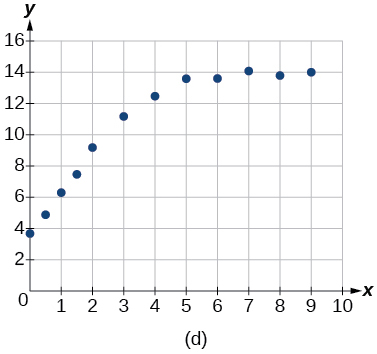
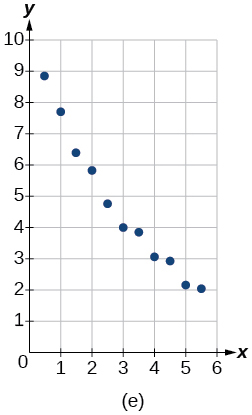
6) y=10.209e^{-0.294x}
7) y=5.598-1.912\ln (x)
- Answer
-
c
8) y=2.104(1.479)^x
9) y=4.607+2.733\ln (x)
- Answer
-
b
10) y=\dfrac{14.005}{1+2.79e^{-0.812x}}
Numeric
11) To the nearest whole number, what is the initial value of a population modeled by the logistic equation P(t)=\dfrac{175}{1+6.995e^{-0.68t}}
- Answer
-
P(0)=22; 175
12) Rewrite the exponential model A(t)=1550(1.085)^x as an equivalent model with base e
13) A logarithmic model is given by the equation h(p)=67.682-5.792\ln (p)
- Answer
-
p\approx 2.67
14) A logistic model is given by the equation P(t)=\dfrac{90}{1+5e^{-0.42t}}
15) What is the y-intercept on the graph of the logistic model given in the previous exercise?
- Answer
-
y-intercept: (0,15)
Technology
For the following exercises, use this scenario: The population P of a koi pond over x months is modeled by the function P(x)=\dfrac{68}{1+16e^{-0.28x}}.
16) Graph the population model to show the population over a span of 3 years.
17) What was the initial population of koi?
- Answer
-
\(4)\ koi
18) How many koi will the pond have after one and a half years?
19) How many months will it take before there are 20 koi in the pond?
- Answer
-
about 6.8 months
20) Use the intersect feature to approximate the number of months it will take before the population of the pond reaches half its carrying capacity.
- Answer
-
For the following exercises, use this scenario: The population P of an endangered species habitat for wolves is modeled by the function P(x)=\dfrac{558}{1+54.8e^{-0.462x}}
21) Graph the population model to show the population over a span of 10 years.
22) What was the initial population of wolves transported to the habitat?
- Answer
-
\(10)\ wolves
23) How many wolves will the habitat have after 3 years?
24) How many years will it take before there are 100 wolves in the habitat?
- Answer
-
about 5.4 years
25) Use the intersect feature to approximate the number of years it will take before the population of the habitat reaches half its carrying capacity.
For the following exercises, refer to Table below.
| x | f(x) |
|---|---|
| 1 | 1125 |
| 2 | 1495 |
| 3 | 2310 |
| 4 | 3294 |
| 5 | 4650 |
| 6 | 6361 |
26) Use a graphing calculator to create a scatter diagram of the data.
- Answer
-
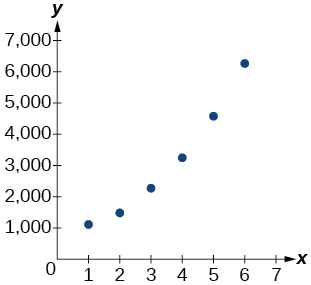
27) Use the regression feature to find an exponential function that best fits the data in the table.
28) Write the exponential function as an exponential equation with base e
- Answer
-
f(x)=776.682e^{0.3549x}
29) Graph the exponential equation on the scatter diagram.
30) Use the intersect feature to find the value of x for which f(x)=4000.
- Answer
-
When f(x)=4000, x\approx 4.6
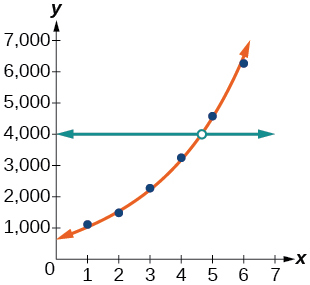
For the following exercises, refer to Table below.
| x | f(x) |
|---|---|
| 1 | 555 |
| 2 | 383 |
| 3 | 307 |
| 4 | 210 |
| 5 | 158 |
| 6 | 122 |
31) Use a graphing calculator to create a scatter diagram of the data.
32) Use the regression feature to find an exponential function that best fits the data in the table.
- Answer
-
f(x)=731.92(0.738)^x
33) Write the exponential function as an exponential equation with base e
34) Graph the exponential equation on the scatter diagram.
- Answer
-
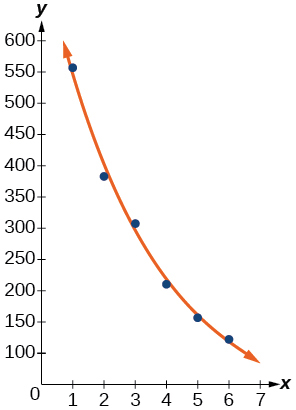
35) Use the intersect feature to find the value of x for which f(x)=250
For the following exercises, refer to Table below.
| x | f(x) |
|---|---|
| 1 | 5.1 |
| 2 | 6.3 |
| 3 | 7.3 |
| 4 | 7.7 |
| 5 | 8.1 |
| 6 | 8.6 |
36) Use a graphing calculator to create a scatter diagram of the data.
- Answer
-
37) Use the LOGarithm option of the REGression feature to find a logarithmic function of the form y=a+b\ln (x) that best fits the data in the table.
38) Use the logarithmic function to find the value of the function when x=10
- Answer
-
f(10)\approx 9.5
39) Graph the logarithmic equation on the scatter diagram.
40) Use the intersect feature to find the value of x for which f(x)=7
- Answer
-
When f(x)=7, x\approx 2.7
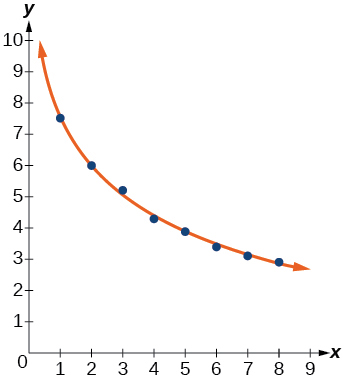
For the following exercises, refer to Table below.
| x | f(x) |
|---|---|
| 1 | 7.5 |
| 2 | 6 |
| 3 | 5.2 |
| 4 | 4.3 |
| 5 | 3.9 |
| 6 | 3.4 |
| 7 | 3.1 |
| 8 | 2.9 |
41) Use a graphing calculator to create a scatter diagram of the data.
42) Use the LOGarithm option of the REGression feature to find a logarithmic function of the form y=a+b\ln (x) that best fits the data in the table.
- Answer
-
f(x)=7.544-2.268\ln (x)
43) Use the logarithmic function to find the value of the function when x=10
44) Graph the logarithmic equation on the scatter diagram.
- Answer
-
45) Use the intersect feature to find the value of x for which f(x)=8
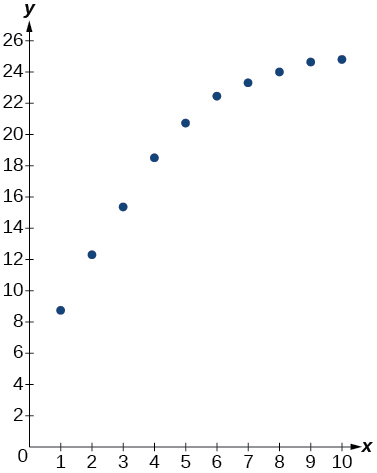
For the following exercises, refer to Table below.
| x | f(x) |
|---|---|
| 1 | 8.7 |
| 2 | 12.3 |
| 3 | 15.4 |
| 4 | 18.5 |
| 5 | 20.7 |
| 6 | 22.5 |
| 7 | 23.3 |
| 8 | 24 |
| 9 | 24.6 |
| 10 | 24.8 |
46) Use a graphing calculator to create a scatter diagram of the data.
- Answer
-
47) Use the LOGISTIC regression option to find a logistic growth model of the form y=\dfrac{c}{1+ae^{-bx}} that best fits the data in the table.
48) Graph the logistic equation on the scatter diagram.
- Answer
-
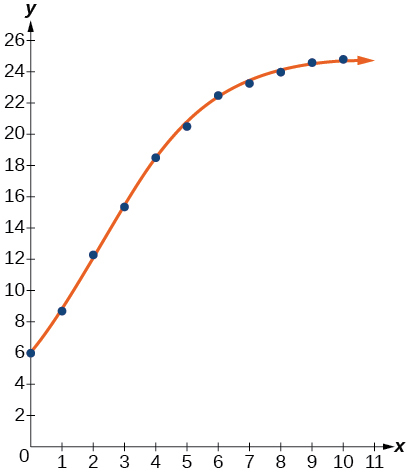
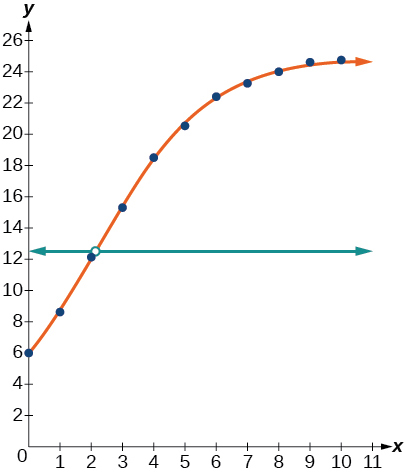
49) To the nearest whole number, what is the predicted carrying capacity of the model?
50) Use the intersect feature to find the value of x for which the model reaches half its carrying capacity.
- Answer
-
When f(x)=12.5, x\approx 2.1
For the following exercises, refer to Table below.
| x | f(x) |
|---|---|
| 0 | 12 |
| 2 | 28.6 |
| 4 | 52.8 |
| 5 | 70.3 |
| 7 | 99.9 |
| 8 | 112.5 |
| 10 | 125.8 |
| 11 | 127.9 |
| 15 | 135.1 |
| 17 | 135.9 |
51) Use a graphing calculator to create a scatter diagram of the data.
52) Use the LOGISTIC regression option to find a logistic growth model of the form y=\dfrac{c}{1+ae^{-bx}} that best fits the data in the table.
- Answer
-
y=\dfrac{136.068}{1+10.324e^{-0.480x}}
53) Graph the logistic equation on the scatter diagram.
54) To the nearest whole number, what is the predicted carrying capacity of the model?
- Answer
-
about 136
55) Use the intersect feature to find the value of x for which the model reaches half its carrying capacity.
Extensions
56) Recall that the general form of a logistic equation for a population is given by P(t)=\dfrac{c}{1+ae^{-bt}}
- Answer
-
Working with the left side of the equation, we see that it can be rewritten as ae^{-bt}
: \begin{align*} \dfrac{c-P(t)}{P(t)} &= \dfrac{c-\frac{c}{1+ae^{-bt}}}{\frac{c}{1+ae^{-bt}}}\\ &= \dfrac{\frac{c\left ( 1+ae^{-bt} \right )-c}{1+ae^{-bt}}}{\frac{c}{1+ae^{-bt}}}\\ &= \dfrac{\frac{c\left ( 1+ae^{-bt} -1\right )}{1+ae^{-bt}}}{\frac{c}{1+ae^{-bt}}}\\ &= 1+ae^{-bt}-1\\ &= ae^{-bt} \end{align*}
\begin{align*} P_0 &= \dfrac{c}{1+ae^{-b(0)}}\\ &= \dfrac{c}{1+a} \end{align*}
Therefore,
\begin{align*} \dfrac{c-P_0}{P_0}e^{-bt} &= \dfrac{c-\frac{c}{1+a}}{\frac{c}{1+a}}e^{-bt}\\ &= \dfrac{\frac{c( 1+a )-c}{1+a}}{\frac{c}{1+a}}e^{-bt}\\ &= \dfrac{\frac{c ( 1+a -1 )}{1+a}}{\frac{c}{1+a}}e^{-bt}\\ &= (1+a-1)e^{-bt}\\ &= ae^{-bt} \end{align*}
Thus,
\dfrac{c-P(t)}{P(t)}=\dfrac{c-P_0}{P_0}e^{-bt}
57) Use a graphing utility to find an exponential regression formula f(x) and a logarithmic regression formula g(x) for the points (1.5,1.5) and (8.5,8.5
58) Verify the conjecture made in the previous exercise. Round all numbers to six decimal places when necessary.
- Answer
-
First rewrite the exponential with base e: f(x)=1.034341e^{0.247800x}
. , \begin{align*} g(f(x)) &= 4.035510\ln\left (1.034341e^{0.247800x}\right )-0.136259\\ &= 4.03551(\ln \left(1.034341)+\ln\left (e^{0.2478x} \right)\right)-0.136259\\ &= 4.03551(\ln(1.034341)+0.2478x)-0.136259\\ &= 0.136257+0.999999x-0.136259\\ &= -0.000002+0.999999x\\ &\approx 0+x \\ &= x \end{align*}
59) Find the inverse function f^{-1}(x) for the logistic function f(x)=\dfrac{c}{1+ae^{-bx}}
60) Use the result from the previous exercise to graph the logistic model P(t)=\dfrac{20}{1+4e^{-0.5t}}
- Answer
-
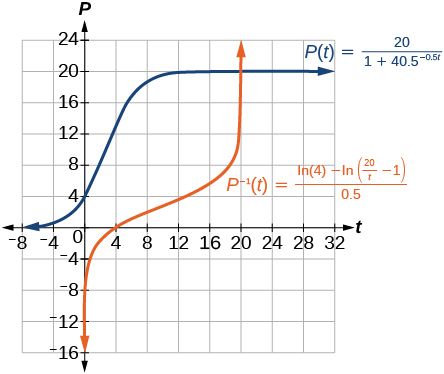
The graph of P(t) has a y-intercept at (0, 4) and horizontal asymptotes at y = 0 and y = 20. The graph of P^{-1}(t) has an x- intercept at (4, 0) and vertical asymptotes at x = 0 and x = 20.
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


