7.6: Modeling with Trigonometric Equations

Suppose we charted the average daily temperatures in New York City over the course of one year. We would expect to find the lowest temperatures in January and February and highest in July and August. This familiar cycle repeats year after year, and if we were to extend the graph over multiple years, it would resemble a periodic function.

Figure $\PageIndex{1}$: The hands on a clock are periodic: they repeat positions every twelve hours. (credit: “zoutedrop”/Flickr)

Many other natural phenomena are also periodic. For example, the phases of the moon have a period of approximately 28 days, and birds know to fly south at about the same time each year. So how can we model an equation to reflect periodic behavior? First, we must collect and record data. We then find a function that resembles an observed pattern. Finally, we make the necessary alterations to the function to get a model that is dependable. In this section, we will take a deeper look at specific types of periodic behavior and model equations to fit data.

Determining the Amplitude and Period of a Sinusoidal Function

Any motion that repeats itself in a fixed time period is considered periodic motion and can be modeled by a sinusoidal function. The amplitude of a sinusoidal function is the distance from the midline to the maximum value, or from the midline to the minimum value. The midline is the average value. Sinusoidal functions oscillate above and below the midline, are periodic, and repeat values in set cycles. Recall from Graphs of the Sine and Cosine Functions that the period of the sine function and the cosine function is $2π$. In other words, for any value of $x$,

$$\sin(x±2πk)=\sin x \; \text{and} \; \cos(x±2πk)=\cos x$$

where $k$ is an integer.

STANDARD FORM OF SINUSOIDAL EQUATIONS

The general forms of a sinusoidal equation are given as

$$y=A \sin(Bt−C)+D$$

or

$$y=A \cos(Bt−C)+D$$

where $\text{amplitude}=|A|,B$ is related to period such that the $\text{period}=\frac{2π}{B},C$ is the phase shift such that $\frac{C}{B}$ denotes the horizontal shift, and $D$ represents the vertical shift from the graph’s parent graph.

Note that the models are sometimes written as

$$y=a \sin (ω t±C)+D$$

or

$$y=a \cos(ω t±C)+D,$$

with a period that is given as $\frac{2π}{ω}$.

The difference between the sine and the cosine graphs is that the sine graph begins with the average value of the function and the cosine graph begins with the maximum or minimum value of the function.

Example $\PageIndex{1}$: Showing How the Properties of a Trigonometric Function Can Transform a Graph

Show the transformation of the graph of $y=\sin x$ into the graph of $y=2 \sin(4x−\frac{π}{2})+2$.

Solution

Consider the series of graphs in Figure $\PageIndex{1}$ and the way each change to the equation changes the image.

Figure $\PageIndex{2}$:

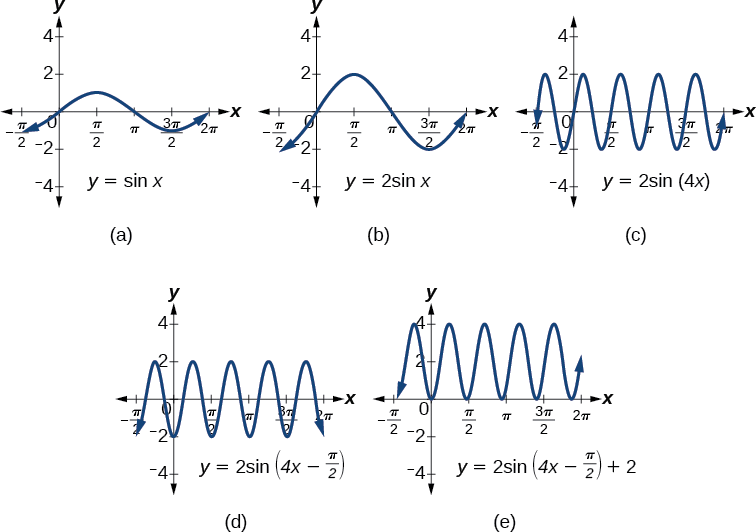
1. The basic graph of $y=\sin x$
2. Changing the amplitude from 1 to 2 generates the graph of $y=2 \sin x$.
3. The period of the sine function changes with the value of $B,$ such that $\text{period}=\frac{2π}{B}.$ Here we have $B=4,$ which translates to a period of $\frac{π}{2}$. The graph completes one full cycle in $\frac{π}{2}$ units.
4. The graph displays a horizontal shift equal to $\frac{C}{B}$, or $\frac{\frac{π}{2}}{4}=\frac{π}{8}$.
5. Finally, the graph is shifted vertically by the value of $D$. In this case, the graph is shifted up by 2 units.

Example $\PageIndex{2}$: Finding the Amplitude and Period of a Function

Find the amplitude and period of the following functions and graph one cycle.

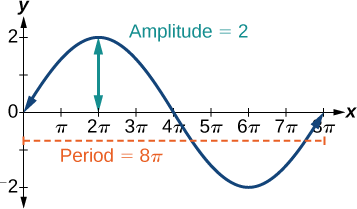
1. $y=2 \sin (\frac{1}{4}x)$
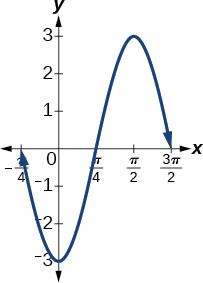
2. $y=−3 \sin (2x+\frac{π}{2})$
3. $y= \cos x+3$

Solution

We will solve these problems according to the models.

1. $y=2 \sin (\frac{1}{4}x)$ involves sine, so we use the form $$y=A \sin (Bt+C)+D \nonumber$$ We know that $| A |$ is the amplitude, so the amplitude is 2. Period is $\frac{2π}{B}$ so the period is $$\begin{align*} \dfrac{2π}{B} &=\dfrac{2π}{\frac{1}{4}} \\ & =8π \end{align*}$$ See the graph in Figure $\PageIndex{3}$.

Figure $\PageIndex{3}$:

2. $y=−3 \sin(2x+ \frac{π}{2})$ involves sine, so we use the form $$y=A \sin (Bt−C)+D \nonumber$$ Amplitude is $| A |$, so the amplitude is $|−3|=3.$ Since $A$ is negative, the graph is reflected over the x-axis. Period is $\frac{2π}{B}$,so the period is $$\dfrac{2π}{B}=\dfrac{2π}{2}=π \nonumber$$ The graph is shifted to the left by $\frac{C}{B}=\frac{\frac{π}{2}}{2}=\frac{π}{4}$ units. See Figure $\PageIndex{4}$.

Figure $\PageIndex{4}$:

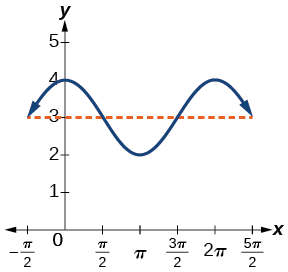
3. $y= \cos x+3$ involves cosine, so we use the form
4. $$y=A \cos (Bt±C)+D \nonumber$$ Amplitude is $| A |$, so the amplitude is 1 and the period is $2π$ (Figure $\PageIndex{5}$. This is the standard cosine function shifted up three units.

Figure $\PageIndex{5}$

Exercise $\PageIndex{1}$:

What are the amplitude and period of the function $y=3 \cos (3πx)$?

Answer

The amplitude is $3,$ and the period is $\frac{2}{3}$.

Finding Equations and Graphing Sinusoidal Functions

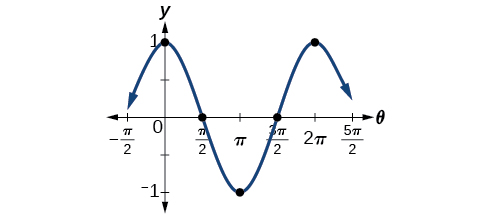
One method of graphing sinusoidal functions is to find five key points. These points will correspond to intervals of equal length representing $\frac{1}{4}$ of the period. The key points will indicate the location of maximum and minimum values. If there is no vertical shift, they will also indicate x-intercepts. For example, suppose we want to graph the function $y=cos θ.$ We know that the period is $2π$, so we find the interval between key points as follows.

$$\frac{2π}{4}=\frac{π}{2} \nonumber$$

Starting with $θ=0,$ we calculate the first y-value, add the length of the interval $\frac{π}{2}$ to $0$, and calculate the second y-value. We then add $\frac{π}{2}$ repeatedly until the five key points are determined. The last value should equal the first value, as the calculations cover one full period. Making a table similar to Table $\PageIndex{1}$, we can see these key points clearly on the graph shown in Figure $\PageIndex{6}$.

Table $\PageIndex{1}$

$θ$	$0$	$\frac{π}{2}$	$π$	$\frac{3π}{2}$	$2π$
$y=\cos θ$	$1$	$0$	−1−1	$0$	$1$

Figure $\PageIndex{6}$

Example $\PageIndex{3}$: Graphing Sinusoidal Functions Using Key Points

Graph the function $y=−4 \cos (πx)$ using amplitude, period, and key points.

Solution

The amplitude is $|−4|=4.$ The period is $\frac{2π}{ω}=\frac{2π}{π}=2.$ (Recall that we sometimes refer to $B$ as $ω.$) One cycle of the graph can be drawn over the interval $[ 0,2 ]$. To find the key points, we divide the period by 4. Make a table similar to Figure $\PageIndex{1}$:, starting with $x=0$ and then adding $\frac{1}{2}$ successively to $x$ and calculate $y.$ See the graph in Figure $\PageIndex{7}$.

Table $\PageIndex{1}$

$x$	$0$	$\frac{1}{2}$	$1$	$\frac{3}{2}$	$2$
$y=−4 \cos(πx)$	$−4$	$0$	$4$	$0$	$−4$

Figure $\PageIndex{7}$

Exercise $\PageIndex{2}$:

Graph the function $y=3 \sin(3x)$ using the amplitude, period, and five key points.

$x$	0	$\frac{π}{6}$	$\frac{π}{3}$	$\frac{π}{2}$	$\frac{2π}{3}$
$3 \sin (3x)$	0	3	0	-3	0

Answer

Figure $\PageIndex{8}$

Modeling Periodic Behavior

We will now apply these ideas to problems involving periodic behavior.

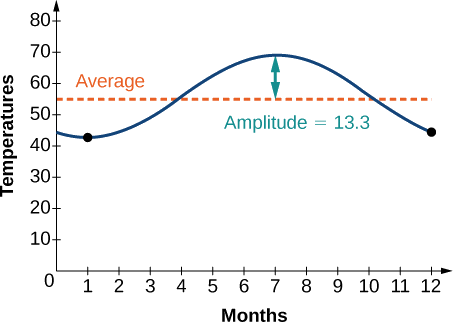
Example $\PageIndex{4}$: Modeling an Equation and Sketching a Sinusoidal Graph to Fit Criteria

The average monthly temperatures for a small town in Oregon are given in Table $\PageIndex{1}$. Find a sinusoidal function of the form $y=A \sin (Bt−C)+D$ that fits the data (round to the nearest tenth) and sketch the graph.

Table $\PageIndex{2}$

Month	Temperature,$^oF$
January	42.5
February	44.5
March	48.5
April	52.5
May	58
June	63
July	68.5
August	69
September	64.5
October	55.5
November	46.5
December	43.5

Solution

Recall that amplitude is found using the formula

$$A=\dfrac{\text{largest value −smallest value}}{2}$$

Thus, the amplitude is

$$\begin{align*} |A| & = \dfrac{69−42.5}{2} \\ &=13.25 \end{align*}$$

The data covers a period of 12 months, so $\frac{2π}{B}=12$ which gives $B=\frac{2π}{12}=\frac{π}{6}$.

The vertical shift is found using the following equation.

$$D=\dfrac{\text{highest value+lowest value}}{2}$$

Thus, the vertical shift is

$$\begin{align*} D &= \dfrac{69+42.5}{2} &=55.8 \end{align*}$$

So far, we have the equation $y=13.3 \sin (\frac{π}{6}x−C)+55.8$.

To find the horizontal shift, we input the $x$ and $y$ values for the first month and solve for $C$.

$$\begin{align*} 42.5 & =13.3 \sin (\frac{π}{6}(1)−C)+55.8 \\ −13.3 & =13.3 \sin (\frac{π}{6}−C) \\ −1 & =\sin (\frac{π}{6}−C) \;\;\;\;\;\;\;\; \sin θ=−1→ θ=−\frac{π}{2} \\ \frac{π}{6}−C=−\frac{π}{2} \\ \frac{π}{6}+\frac{π}{2} & =C \\ &=\frac{2π}{3} \end{align*}$$

We have the equation $y=13.3 \sin (\frac{π}{6}x−\frac{2π}{3})+55.8$. See the graph in Figure $\PageIndex{9}$.

Figure $\PageIndex{9}$

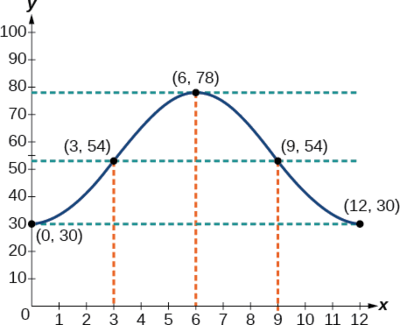
Example $\PageIndex{5}$: Describing Periodic Motion

The hour hand of the large clock on the wall in Union Station measures 24 inches in length. At noon, the tip of the hour hand is 30 inches from the ceiling. At 3 PM, the tip is 54 inches from the ceiling, and at 6 PM, 78 inches. At 9 PM, it is again 54 inches from the ceiling, and at midnight, the tip of the hour hand returns to its original position 30 inches from the ceiling. Let $y$ equal the distance from the tip of the hour hand to the ceiling $x$ hours after noon. Find the equation that models the motion of the clock and sketch the graph.

Solution

Begin by making a table of values as shown in Table $\PageIndex{3}$.

Table $\PageIndex{3}$

$x$	$y$	Points to plot
Noon	30 in	$(0,30)$
3 PM	54 in	$(3,54)$
6 PM	78 in	$(6,78)$
9 PM	54 in	$(9,54)$
Midnight	30 in	$(12,30)$

To model an equation, we first need to find the amplitude.

$$\begin{align*} | A | & =| \dfrac{78−30}{2} | \\ &=24 \end{align*}$$

The clock’s cycle repeats every 12 hours. Thus,

$$\begin{align*} B &=\dfrac{2π}{12} \\ &= \dfrac{π}{6} \end{align*}$$

The vertical shift is

$$\begin{align*} D & = \dfrac{78+30}{2} \\ &=54 \end{align*}$$

There is no horizontal shift, so $C=0.$ Since the function begins with the minimum value of $y$ when $x=0$ (as opposed to the maximum value), we will use the cosine function with the negative value for $A$. In the form $y=A \cos (Bx±C)+D,$ the equation is

$$y=−24 \cos (\dfrac{π}{6}x)+54$$

See Figure $\PageIndex{10}$.

Figure $\PageIndex{10}$

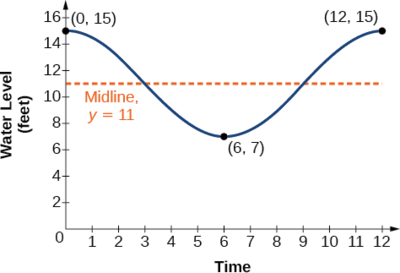
Example $\PageIndex{6}$: Determining a Model for Tides

The height of the tide in a small beach town is measured along a seawall. Water levels oscillate between 7 feet at low tide and 15 feet at high tide. On a particular day, low tide occurred at 6 AM and high tide occurred at noon. Approximately every 12 hours, the cycle repeats. Find an equation to model the water levels.

Solution

As the water level varies from 7 ft to 15 ft, we can calculate the amplitude as

$$\begin{align*} |A| &=| \frac{(15−7)}{2} | \\ & =4 \end{align*}$$

The cycle repeats every 12 hours; therefore, $B$ is

$$\begin{align*} \dfrac{2π}{12}=\dfrac{π}{6} \end{align*}$$

There is a vertical translation of $\frac{(15+8)}{2}=11.5$. Since the value of the function is at a maximum at $t=0$, we will use the cosine function, with the positive value for $A$.

$$y=4 \cos (\dfrac{π}{6}) t+11 \nonumber$$

See Figure $\PageIndex{11}$.

Figure $\PageIndex{11}$

Exercise $\PageIndex{3}$:

The daily temperature in the month of March in a certain city varies from a low of $24°F$ to a high of $40°F.$ Find a sinusoidal function to model daily temperature and sketch the graph. Approximate the time when the temperature reaches the freezing point $32 °F.$ Let $t=0$ correspond to noon.

Answer

$$y=8 \sin (\frac{π}{12}t)+32 \nonumber$$

The temperature reaches freezing at noon and at midnight.

Exercise $\PageIndex{4}$: Interpreting the Periodic Behavior Equation

The average person’s blood pressure is modeled by the function $f(t)=20 \sin (160πt)+100$, where $f(t)$ represents the blood pressure at time $t$, measured in minutes. Interpret the function in terms of period and frequency. Sketch the graph and find the blood pressure reading.

Analysis

Blood pressure of $\frac{120}{80}$ is considered to be normal. The top number is the maximum or systolic reading, which measures the pressure in the arteries when the heart contracts. The bottom number is the minimum or diastolic reading, which measures the pressure in the arteries as the heart relaxes between beats, refilling with blood. Thus, normal blood pressure can be modeled by a periodic function with a maximum of 120 and a minimum of 80.

Example $\PageIndex{7}$: Interpreting the Periodic Behavior Equation

The average person’s blood pressure is modeled by the function $f(t)=20 \sin (160πt)+100$, where $f(t)$ represents the blood pressure at time $t$, measured in minutes. Interpret the function in terms of period and frequency. Sketch the graph and find the blood pressure reading.

Solution

The period is given by

$$\begin{align*} \dfrac{2π}{ω} & = \dfrac{2π}{160π} \\ &=\dfrac{1}{80} \end{align*}$$

In a blood pressure function, frequency represents the number of heart beats per minute. Frequency is the reciprocal of period and is given by

$$\begin{align*} \dfrac{ω}{2π} & = \dfrac{160π}{2π} \\ & =80 \end{align*}$$

Figure $\PageIndex{12}$: The blood pressure reading on the graph is $\frac{120}{80} (\frac{\text{maximum}}{\text{minimum}})$.

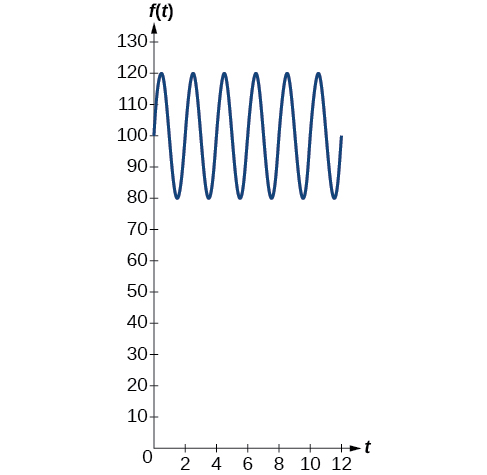
Analysis

Blood pressure of $\frac{120}{80}$ is considered to be normal. The top number is the maximum or systolic reading, which measures the pressure in the arteries when the heart contracts. The bottom number is the minimum or diastolic reading, which measures the pressure in the arteries as the heart relaxes between beats, refilling with blood. Thus, normal blood pressure can be modeled by a periodic function with a maximum of 120 and a minimum of 80.

Modeling Harmonic Motion Functions

Harmonic motion is a form of periodic motion, but there are factors to consider that differentiate the two types. While general periodic motion applications cycle through their periods with no outside interference, harmonic motion requires a restoring force. Examples of harmonic motion include springs, gravitational force, and magnetic force.

Simple Harmonic Motion

A type of motion described as simple harmonic motion involves a restoring force but assumes that the motion will continue forever. Imagine a weighted object hanging on a spring, When that object is not disturbed, we say that the object is at rest, or in equilibrium. If the object is pulled down and then released, the force of the spring pulls the object back toward equilibrium and harmonic motion begins. The restoring force is directly proportional to the displacement of the object from its equilibrium point. When $t=0,d=0.$

SIMPLE HARMONIC MOTION

We see that simple harmonic motion equations are given in terms of displacement:

$$d=a \cos (ωt) \; \text{or} \; d=a \sin (ωt)$$

where $| a |$ is the amplitude, $\frac{2π}{ω}$ is the period, and $\frac{ω}{2π}$ is the frequency, or the number of cycles per unit of time.

Exercise $\PageIndex{5}$: Finding the Displacement, Period, and Frequency, and Graphing a Function

For each the given functions:

1. $y=5 \sin (3t)$
2. $y=6 \cos (πt)$
3. $y=5 \cos (\frac{π}{2}) t$

address the following questions:

1. Find the maximum displacement of an object.
2. Find the period or the time required for one vibration.
3. Find the frequency.
4. Sketch the graph.

Figure $\PageIndex{13}$

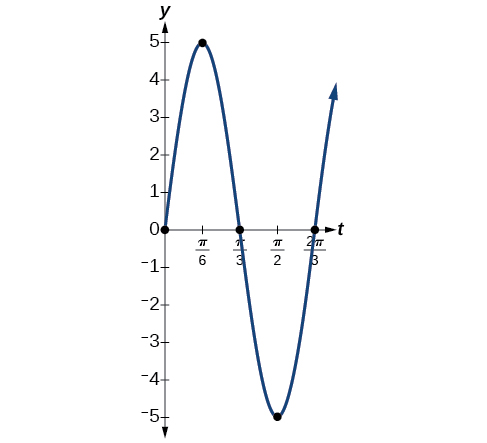
Answer a

1. The maximum displacement is equal to the amplitude,$|a|$, which is 5.
2. The period is $\frac{2π}{ω}=\frac{2π}{3}$.
3. The frequency is given as $\frac{ω}{2π}=\frac{3}{2π}$.
4. See Figure $\PageIndex{13}$. The graph indicates the five key points.

Answer b

1. The maximum displacement is $6$.
2. The period is $\frac{2π}{ω}=\frac{2π}{π}=2.$
3. The frequency is $\frac{ω}{2π}=\frac{π}{2π}=\frac{1}{2}.$
4. See Figure $\PageIndex{14}$.

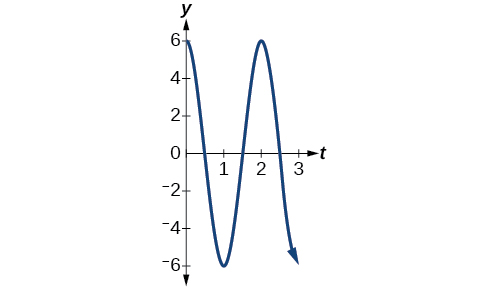
Figure $\PageIndex{14}$

Answer c

1. The maximum displacement is $5$.
2. The period is $\frac{2π}{ω}=\frac{2π}{\frac{π}{2}}=4$.
3. The frequency is $\frac{1}{4}.$
4. See Figure $\PageIndex{15}$.

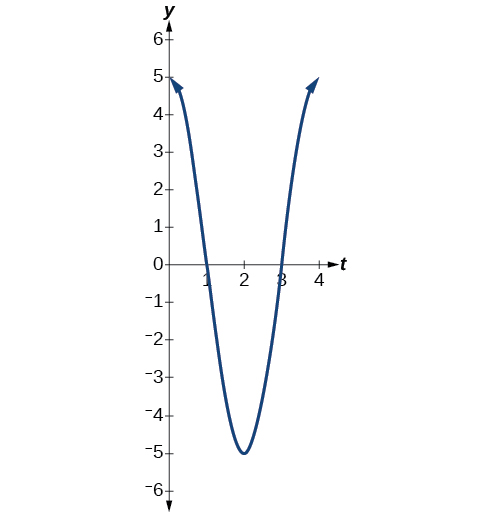
Figure $\PageIndex{15}$

Damped Harmonic Motion

In reality, a pendulum does not swing back and forth forever, nor does an object on a spring bounce up and down forever. Eventually, the pendulum stops swinging and the object stops bouncing and both return to equilibrium. Periodic motion in which an energy-dissipating force, or damping factor, acts is known as damped harmonic motion. Friction is typically the damping factor.

In physics, various formulas are used to account for the damping factor on the moving object. Some of these are calculus-based formulas that involve derivatives. For our purposes, we will use formulas for basic damped harmonic motion models.

Definition: DAMPED HARMONIC MOTION

In damped harmonic motion, the displacement of an oscillating object from its rest position at time $t$ is given as

$$f(t)=ae^{−ct} \sin (ωt) \; \text{ or} \; f(t)=ae^{−ct} \cos (ωt)$$

where $c$ is a damping factor, $|a|$ is the initial displacement and $\frac{2π}{ω}$ is the period.

Example $\PageIndex{8}$: Modeling Damped Harmonic Motion

Model the equations that fit the two scenarios and use a graphing utility to graph the functions: Two mass-spring systems exhibit damped harmonic motion at a frequency of 0.5 cycles per second. Both have an initial displacement of 10 cm. The first has a damping factor of 0.5 and the second has a damping factor of 0.1.

Solution

At time $t=0$, the displacement is the maximum of 10 cm, which calls for the cosine function. The cosine function will apply to both models.

We are given the frequency $f=\frac{ω}{2π}$ of 0.5 cycles per second. Thus,

$$\begin{align*} \dfrac{ω}{2π} &=0.5 \\ ω&=(0.5)2π \\ &=π \end{align*}$$

The first spring system has a damping factor of $c=0.5$. Following the general model for damped harmonic motion, we have

$$f(t)=10e^{−0.5t} \cos (πt) \nonumber$$

Figure $\PageIndex{16}$ models the motion of the first spring system.

Figure $\PageIndex{16}$

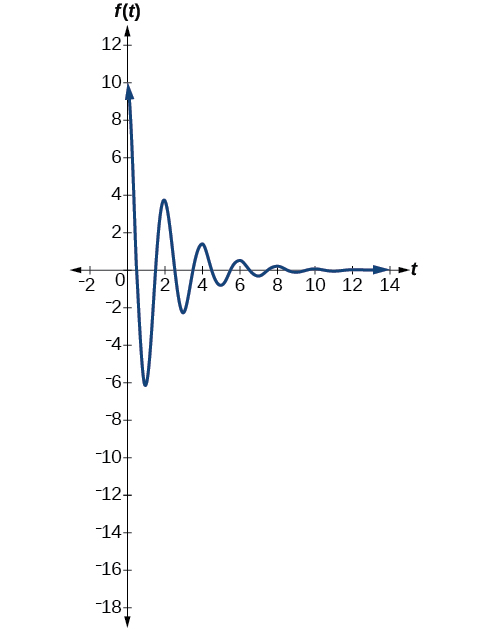
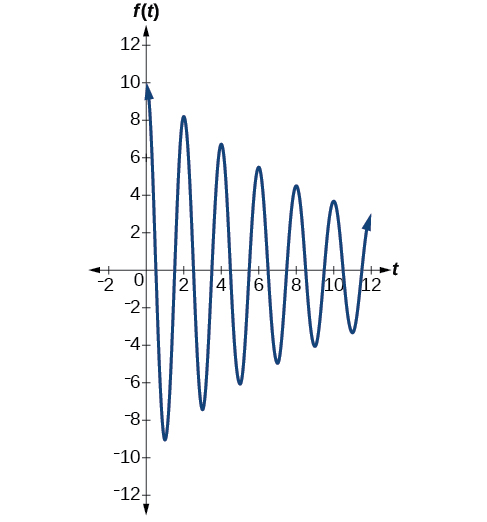
The second spring system has a damping factor of $c=0.1$ and can be modeled as

$$f(t)=10e^{−0.1t} \cos (πt)$$

Figure $\PageIndex{17}$ models the motion of the second spring system.

Figure $\PageIndex{17}$

Analysis

Notice the differing effects of the damping constant. The local maximum and minimum values of the function with the damping factor $c=0.5$ decreases much more rapidly than that of the function with $c=0.1$.

Exercise $\PageIndex{6}$: Finding a Cosine Function that Models Damped Harmonic Motion

Find and graph a function of the form $y=ae^{−ct} \cos (ωt)$ that models the information given.

1. $a=20,c=0.05,p=4$
2. $a=2,c=1.5,f=3$

Solution

Substitute the given values into the model. Recall that period is $\frac{2π}{ω}$ and frequency is $\frac{ω}{2π}$.

1. $y=20e^{−0.05t} \cos (\frac{π}{2}t).$ See Figure $\PageIndex{18}$.

   

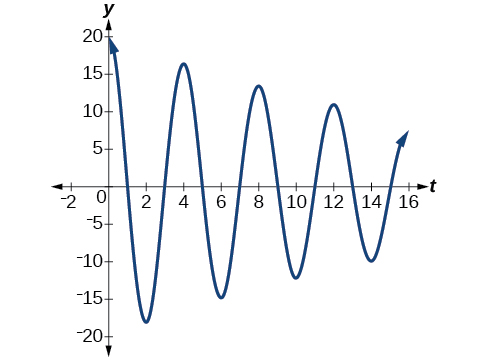
   Figure $\PageIndex{18}$

2. $y=2e^{−1.5t} \cos (6πt).$ See Figure $\PageIndex{19}$.

   

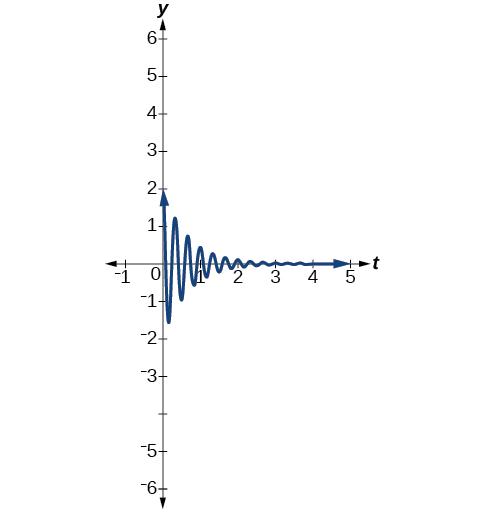
   Figure $\PageIndex{19}$

Exercise $\PageIndex{7}$

The following equation represents a damped harmonic motion model: $f(t)=5e^{−6t} \cos (4t)$ Find the initial displacement, the damping constant, and the frequency.

Answer

initial displacement =6, damping constant = -6, frequency =$\frac{2}{π}$

Example $\PageIndex{9}$: Finding a Sine Function that Models Damped Harmonic Motion

Find and graph a function of the form $y=ae^{−ct} \sin (ωt)$ that models the information given.

1. $a=7,c=10,p=\frac{π}{6}$
2. $a=0.3,c=0.2,f=20$

Solution

Calculate the value of $ω$ and substitute the known values into the model.

1. As period is $\frac{2π}{ω}$, we have

   $$\begin{align*} \dfrac{π}{6} &=\dfrac{2π}{ω} \\ ωπ &=6(2π) \\ ω &=12 \end{align*}$$

   The damping factor is given as 10 and the amplitude is 7. Thus, the model is $y=7e^{−10t} \sin (12t)$. See Figure $\PageIndex{20}$.

   

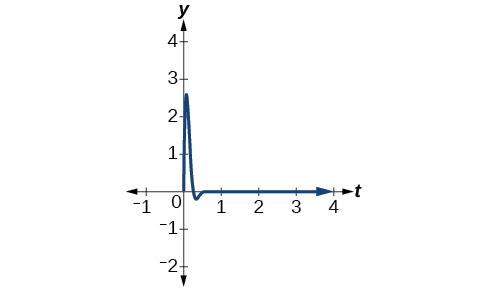
   Figure $\PageIndex{20}$

2. As frequency is $\frac{ω}{2π}$, we have

   $$\begin{align*} 20 &=\dfrac{ω}{2π} \\ 40π &=ω \end{align*}$$

   The damping factor is given as $0.2$ and the amplitude is $0.3.$ The model is $y=0.3e^{−0.2t} \sin (40πt).$ See Figure $\PageIndex{21}$.

   

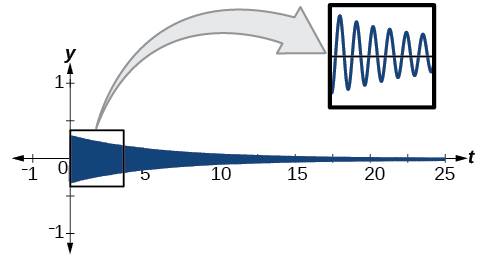
   Figure $\PageIndex{21}$

Analysis

A comparison of the last two examples illustrates how we choose between the sine or cosine functions to model sinusoidal criteria. We see that the cosine function is at the maximum displacement when $t=0$, and the sine function is at the equilibrium point when $t=0.$ For example, consider the equation $y=20e^{−0.05t} \cos (\frac{π}{2}t)$ from Example. We can see from the graph that when $t=0,y=20,$ which is the initial amplitude. Check this by setting $t=0$ in the cosine equation:

$$\begin{align*} y &=20e^{−0.05(0)} \cos (\frac{π}{2})(0) \\ &=20(1)(1) \\ & =20 \end{align*}$$

Using the sine function yields

$$\begin{align*} y &=20e^{−0.05(0)} \sin (\frac{π}{2})(0) \\ & =20(1)(0) \\ &=0 \end{align*}$$

Thus, cosine is the correct function.

Exercise $\PageIndex{8}$:

Write the equation for damped harmonic motion given $a=10,c=0.5$, and $p=2.$

Answer

$y=10e^{−0.5t} \cos (πt)$

Example $\PageIndex{10}$: Modeling the Oscillation of a Spring

A spring measuring 10 inches in natural length is compressed by 5 inches and released. It oscillates once every 3 seconds, and its amplitude decreases by 30% every second. Find an equation that models the position of the spring $t$ seconds after being released.

Solution

The amplitude begins at 5 in. and deceases 30% each second. Because the spring is initially compressed, we will write A as a negative value. We can write the amplitude portion of the function as

$$A(t)=5(1−0.30)^t \nonumber$$

We put $(1−0.30)^t$ in the form $e^{ct}$ as follows:

$$\begin{align*} 0.7 &=e^c \\ c &= \ln .7 \\ c & =−0.357 \end{align*}$$

Now let’s address the period. The spring cycles through its positions every 3 seconds, this is the period, and we can use the formula to find omega.

$$\begin{align*} 3 &= \dfrac{2π}{ω} \\ ω &= \dfrac{2π}{3} \end{align*}$$

The natural length of 10 inches is the midline. We will use the cosine function, since the spring starts out at its maximum displacement. This portion of the equation is represented as

$$y=\cos (\dfrac{2π}{3}t)+10 \nonumber$$

Finally, we put both functions together. Our the model for the position of the spring at $t$ seconds is given as

$$y=−5e^{−0.357t} \cos (\dfrac{2π}{3}t)+10 \nonumber$$

See the graph in Figure $\PageIndex{22}$.

Figure $\PageIndex{22}$

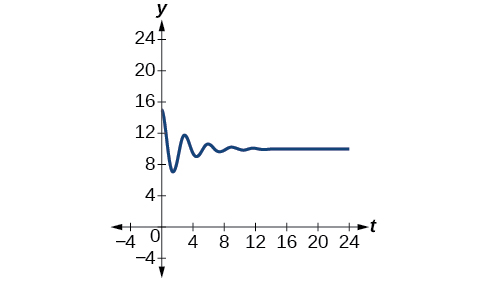
Exercise $\PageIndex{9}$

A mass suspended from a spring is raised a distance of 5 cm above its resting position. The mass is released at time $t=0$ and allowed to oscillate. After $\frac{1}{3}$ second, it is observed that the mass returns to its highest position. Find a function to model this motion relative to its initial resting position.

Answer

$y=5 \cos (6πt)$

According to the Given Criteria

A guitar string is plucked and vibrates in damped harmonic motion. The string is pulled and displaced 2 cm from its resting position. After 3 seconds, the displacement of the string measures 1 cm. Find the damping constant.

Solution

The displacement factor represents the amplitude and is determined by the coefficient $ae^{−ct}$ in the model for damped harmonic motion. The damping constant is included in the term $e^{−ct}$. It is known that after 3 seconds, the local maximum measures one-half of its original value. Therefore, we have the equation

$$ae^{−c(t+3)}=\dfrac{1}{2} ae^{−ct}$$

Use algebra and the laws of exponents to solve for $c$.

$$\begin{array}{cl} ae^{−c(t+3)}=\frac{1}{2}ae^{−ct} \\ e^{−ct}⋅e^{−3c}=\frac{1}{2}e^{−ct} & \text{Divide out } a. \\ e^{−3c}=\frac{1}{2} & \text{Divide out }e^{−ct}. \\ e^{3c}=2 & \text{Take reciprocals.} \end{array}$$

Then use the laws of logarithms.

$$\begin{align*} e^{3c} &=2 \\ 3c &=\ln 2 \\ c & =\frac{\ln 2}{3} \end{align*}$$

The damping constant is $\frac{\ln 2}{3}$.

Bounding Curves in Harmonic Motion

Harmonic motion graphs may be enclosed by bounding curves. When a function has a varying amplitude, such that the amplitude rises and falls multiple times within a period, we can determine the bounding curves from part of the function.

Example $\PageIndex{12}$: Graphing an Oscillating Cosine Curve

Graph the function $f(x)=\cos (2πx) \cos (16πx)$.

Solution

The graph produced by this function will be shown in two parts. The first graph will be the exact function $f(x)$ (see Figure $\PageIndex{23; top}$;), and the second graph is the exact function $f(x)$ plus a bounding function (see Figure $\PageIndex{23; bottom}$). The graphs look quite different.

Figure_07_07_016.jpg" />

Figure $\PageIndex{23}$

Analysis

The curves $y=\cos (2πx)$ and $y=−\cos (2πx)$ are bounding curves: they bound the function from above and below, tracing out the high and low points. The harmonic motion graph sits inside the bounding curves. This is an example of a function whose amplitude not only decreases with time, but actually increases and decreases multiple times within a period.

Key Equations

Standard form of sinusoidal equation	$y=A \sin (Bt−C)+D \text{ or } y=A \cos (Bt−C)+D$
Simple harmonic motion	$d=a \cos (ωt) \text{ or } d=a \sin (ωt)$
Damped harmonic motion	$f(t)=ae^{−ct} \sin (ωt) \text{ or } f(t)=ae^{−ct} \cos (ωt)$

Key Concepts

• Sinusoidal functions are represented by the sine and cosine graphs. In standard form, we can find the amplitude, period, and horizontal and vertical shifts. See Example and Example.
• Use key points to graph a sinusoidal function. The five key points include the minimum and maximum values and the midline values. See Example.
• Periodic functions can model events that reoccur in set cycles, like the phases of the moon, the hands on a clock, and the seasons in a year. See Example, Example, Example and Example.
• Harmonic motion functions are modeled from given data. Similar to periodic motion applications, harmonic motion requires a restoring force. Examples include gravitational force and spring motion activated by weight. See Example.
• Damped harmonic motion is a form of periodic behavior affected by a damping factor. Energy dissipating factors, like friction, cause the displacement of the object to shrink. See Example, Example, Example, Example, and Example.
• Bounding curves delineate the graph of harmonic motion with variable maximum and minimum values. See Example.