While it is convenient to describe the location of a point on a circle using an angle or a distance along the circle, relating this information to the x and y coordinates and the circle equation we explored in Section 5.1 is an important application of trigonometry.
A distress signal is sent from a sailboat during a storm, but the transmission is unclear and the rescue boat sitting at the marina cannot determine the sailboat’s location. Using high powered radar, they determine the distress signal is coming from a distance of 20 miles at an angle of 225 degrees from the marina. How many miles east/west and north/south of the rescue boat is the stranded sailboat?
In a general sense, to investigate this, we begin by drawing a circle centered at the origin with radius \(r\)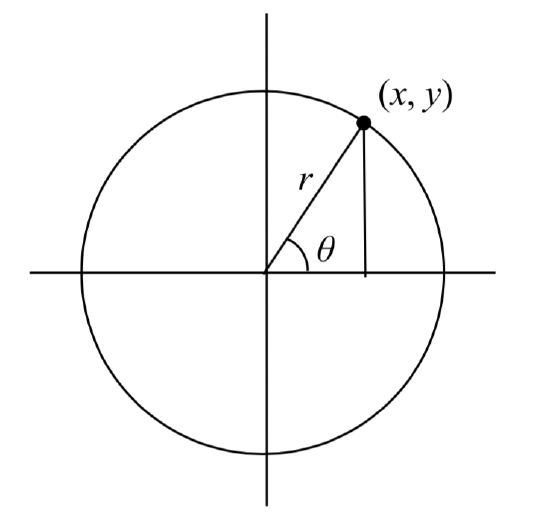 , and marking the point on the circle indicated by some angle \(\theta\). This point has coordinates (\(x\), \(y\)).
, and marking the point on the circle indicated by some angle \(\theta\). This point has coordinates (\(x\), \(y\)).
If we drop a line segment vertically down from this point to the x axis, we would form a right triangle inside of the circle.
No matter which quadrant our angle \(\theta\) puts us in we can draw a triangle by dropping a perpendicular line segment to the \(x\) axis, keeping in mind that the values of \(x\) and \(y\) may be positive or negative, depending on the quadrant.
Additionally, if the angle \(\theta\) puts us on an axis, we simply measure the radius as the \(x\) or \(y\) with the other value being 0, again ensuring we have appropriate signs on the coordinates based on the quadrant.
Triangles obtained from different radii will all be similar triangles, meaning corresponding sides scale proportionally. While the lengths of the sides may change, as we saw in the last section, the ratios of the side lengths will always remain constant for any given angle.
\(\dfrac{y_{1} }{r_{1} } =\dfrac{y_{2} }{r_{2} }\) 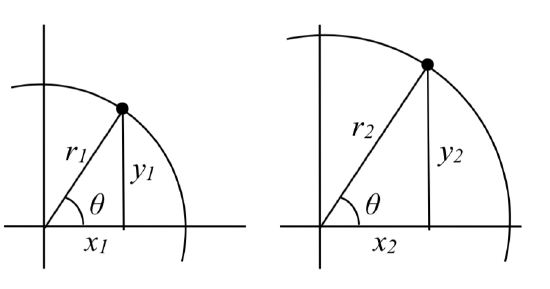
\(\dfrac{x_{1} }{r_{1} } =\dfrac{x_{2} }{r_{2} }\)
To be able to refer to these ratios more easily, we will give them names. Since the ratios depend on the angle, we will write them as functions of the angle \(\theta\).
Note: sine and cosine
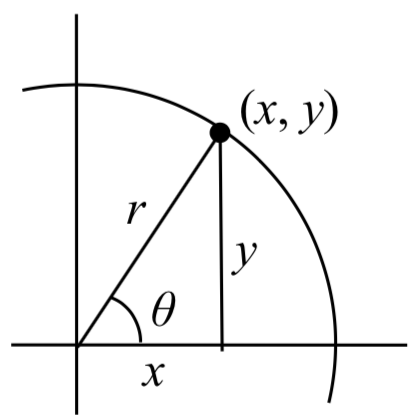 For the point (\(x\), \(y\)) on a circle of radius \(r\) at an angle of \(\theta\), we can define two important functions as the ratios of the sides of the corresponding triangle:
For the point (\(x\), \(y\)) on a circle of radius \(r\) at an angle of \(\theta\), we can define two important functions as the ratios of the sides of the corresponding triangle:
The sine function: \(\sin (\theta )=\dfrac{y}{r}\)
The cosine function: \(\cos (\theta )=\dfrac{x}{r}\)
In this chapter, we will explore these functions using both circles and right triangles. In the next chapter, we will take a closer look at the behavior and characteristics of the sine and cosine functions.
Example \(\PageIndex{1}\)
The point (3, 4) is on the circle of radius 5 at some angle \(\theta\). Find \(\cos (\theta )\)and \(\sin (\theta )\).
Solution
Knowing the radius of the circle and coordinates of the point, we can evaluate the cosine and sine functions as the ratio of the sides.
\[\cos (\theta )=\dfrac{x}{r} =\dfrac{3}{5} \sin (\theta )=\dfrac{y}{r} =\dfrac{4}{5}\nonumber\]
There are a few cosine and sine values which we can determine fairly easily because the corresponding point on the circle falls on the \(x\) or \(y\) axis.
Example \(\PageIndex{2}\)
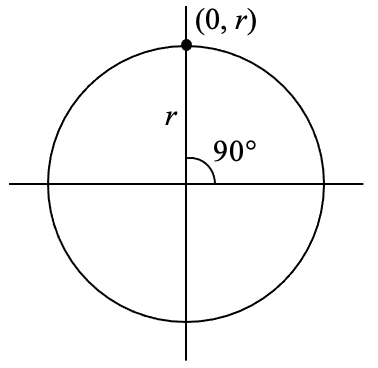
Find \(\cos (90{}^\circ )\) and \(\sin (90{}^\circ )\).
Solution
On any circle, the terminal side of a 90 degree angle points straight up, so the coordinates of the corresponding point on the circle would be (0, r). Using our definitions of cosine and sine,
\[\cos (90{}^\circ )=\dfrac{x}{r} =\dfrac{0}{r} =0\nonumber\]
\[\sin (90{}^\circ )=\dfrac{y}{r} =\dfrac{r}{r} =1\nonumber\]
Exercise \(\PageIndex{1}\)
Find cosine and sine of the angle \(\pi\).
- Answer
-
\[\cos (\pi )=-1 \sin (\pi )=0\nonumber\]
Notice that the definitions above can also be stated as:
coordinates of the point on a circle at a given angle
On a circle of radius \(r\) at an angle of \(\theta\), we can find the coordinates of the point (\(x\), \(y\)) Circles:Points on a Circle at that angle using
\[x=r\cos (\theta )\]
\[y=r\sin (\theta )\]
On a unit circle, a circle with radius 1, \(x=\cos (\theta )\) and \(y=\sin (\theta )\).
Utilizing the basic equation for a circle centered at the origin, \(x^{2} +y^{2} =r^{2}\), combined with the relationships above, we can establish a new identity.
\[x^{2} +y^{2} =r^{2}\nonumber\] substituting the relations above,
\[(r\cos (\theta ))^{2} +(r\sin (\theta ))^{2} =r^{2}\nonumber\] simplifying,
\[r^{2} (\cos (\theta ))^{2} +r^{2} (\sin (\theta ))^{2} =r^{2}\nonumber\] dividing by \(r^{2}\)
\[(\cos (\theta ))^{2} +(\sin (\theta ))^{2} =1\nonumber\] or using shorthand notation
\[\cos ^{2} (\theta )+\sin ^{2} (\theta )=1\nonumber\]
Here \(\cos ^{2} (\theta )\) is a commonly used shorthand notation for \((\cos (\theta ))^{2}\). Be aware that many calculators and computers do not understand the shorthand notation.
In Section 5.1 we related the Pythagorean Theorem \(a^{2} +b^{2} =c^{2}\) to the basic equation of a circle \(x^{2} +y^{2} =r^{2}\), which we have now used to arrive at the Pythagorean Identity.
pythagorean indentity
The Pythagorean Identity. For any angle \(\theta\), \[\cos ^{2} (\theta )+\sin ^{2} (\theta )=1\nonumber\]
One use of this identity is that it helps us to find a cosine value of an angle if we know the sine value of that angle or vice versa. However, since the equation will yield two possible values, we will need to utilize additional knowledge of the angle to help us find the desired value.
Example \(\PageIndex{3}\)
If \(\sin (\theta )=\dfrac{3}{7}\) and \(\theta\) is in the second quadrant, find \(\cos (\theta )\).
Solution
Substituting the known value for sine into the Pythagorean identity,
\[\cos ^{2} (\theta )+\sin ^{2} (\theta )=1\nonumber\]
\[\cos ^{2} (\theta )+\dfrac{9}{49} =1\nonumber\]
\[\cos ^{2} (\theta )=\dfrac{40}{49}\nonumber\]
\[\cos (\theta )=\pm \sqrt{\dfrac{40}{49} } =\pm \dfrac{\sqrt{40} }{7} =\pm \dfrac{2\sqrt{10} }{7}\nonumber\]
Since the angle is in the second quadrant, we know the \(x\) value of the point would be negative, so the cosine value should also be negative. Using this additional information, we can conclude that \[\cos (\theta )=-\dfrac{2\sqrt{10} }{7}\nonumber\]
Values for Sine and Cosine
At this point, you may have noticed that we haven’t found any cosine or sine values from angles not on an axis. To do this, we will need to utilize our knowledge of triangles.
First, consider a point on a circle at an angle of 45 de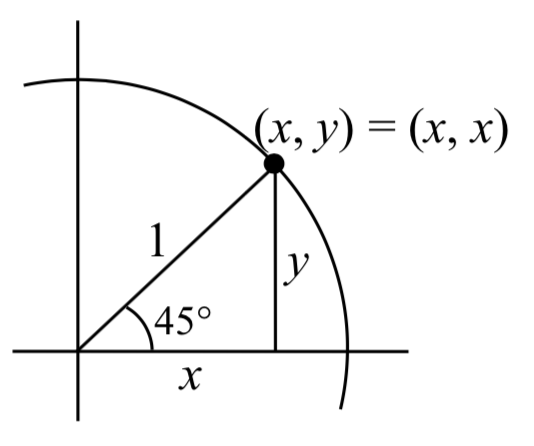 grees, or \(\dfrac{\pi }{4}\). At this angle, the x and y coordinates of the corresponding point on the circle will be equal because 45 degrees divides the first quadrant in half. Since the \(x\) and \(y\) values will be the same, the sine and cosine values will also be equal. Utilizing the Pythagorean Identity,
grees, or \(\dfrac{\pi }{4}\). At this angle, the x and y coordinates of the corresponding point on the circle will be equal because 45 degrees divides the first quadrant in half. Since the \(x\) and \(y\) values will be the same, the sine and cosine values will also be equal. Utilizing the Pythagorean Identity,
\[\cos ^{2} \left(\dfrac{\pi }{4} \right)+\sin ^{2} \left(\dfrac{\pi }{4} \right)=1\nonumber\]
since the sine and cosine are equal, we can substitute sine with cosine
\[\cos ^{2} \left(\dfrac{\pi }{4} \right)+\cos ^{2} \left(\dfrac{\pi }{4} \right)=1\nonumber\] add like terms
\[2\cos ^{2} \left(\dfrac{\pi }{4} \right)=1\nonumber\] divide
\[\cos ^{2} \left(\dfrac{\pi }{4} \right)=\dfrac{1}{2}\nonumber\] since the \(x\) value is positive, we’ll keep the positive root
\[\cos \left(\dfrac{\pi }{4} \right)=\sqrt{\dfrac{1}{2} }\nonumber\] often this value is written with a rationalized denominator
Remember, to rationalize the denominator we multiply by a term equivalent to 1 to get rid of the radical in the denominator.
\[\cos \left(\dfrac{\pi }{4} \right)=\sqrt{\dfrac{1}{2} } \sqrt{\dfrac{2}{2} } =\sqrt{\dfrac{2}{4} } =\dfrac{\sqrt{2} }{2}\nonumber\]
Since the sine and cosine are equal, \(\sin \left(\dfrac{\pi }{4} \right)=\dfrac{\sqrt{2} }{2}\) as well. The (\(x\), \(y\)) coordinates for a point on a circle of radius 1 at an angle of 45 degrees are \(\left(\dfrac{\sqrt{2} }{2} ,\dfrac{\sqrt{2} }{2} \right)\).
Example \(\PageIndex{4}\)
Find the coordinates of the point on a circle of radius 6 at an angle of \(\dfrac{\pi }{4}\).
Solution
Using our new knowledge that \(\sin \left(\dfrac{\pi }{4} \right)=\dfrac{\sqrt{2} }{2}\) and \(\cos \left(\dfrac{\pi }{4} \right)=\dfrac{\sqrt{2} }{2}\), along with our relationships that stated \(x=r\cos (\theta )\) and \(y=r\sin (\theta )\), we can find the coordinates of the point desired:
\[x=6\cos \left(\dfrac{\pi }{4} \right)=6\left(\dfrac{\sqrt{2} }{2} \right)=3\sqrt{2}\nonumber \] \[y=6\sin \left(\dfrac{\pi }{4} \right)=6\left(\dfrac{\sqrt{2} }{2} \right)=3\sqrt{2}\nonumber\]
Exercise \(\PageIndex{2}\)
Find the coordinates of the point on a circle of radius 3 at an angle of \(90{}^\circ\).
- Answer
-
\[\begin{array}{l} {x=3\cos \left(\dfrac{\pi }{2} \right)=3\cdot 0=0} \\ {y=3\sin \left(\dfrac{\pi }{2} \right)=3\cdot 1=3} \end{array}\nonumber\]
Next, we will find the cosine and sine at an angle of 30 degrees, or \(\frac{\pi }{6}\)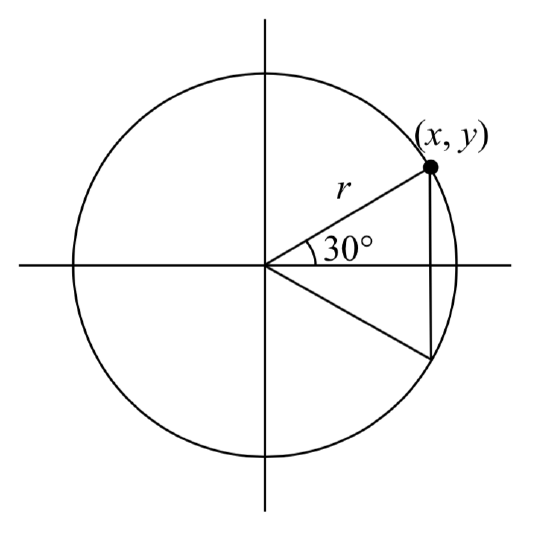 . To do this, we will first draw a triangle inside a circle with one side at an angle of 30 degrees, and another at an angle of -30 degrees. If the resulting two right triangles are combined into one large triangle, notice that all three angles of this larger triangle will be 60 degrees.
. To do this, we will first draw a triangle inside a circle with one side at an angle of 30 degrees, and another at an angle of -30 degrees. If the resulting two right triangles are combined into one large triangle, notice that all three angles of this larger triangle will be 60 degrees.
Since all the angles are equal, the sides will all be equal as well. The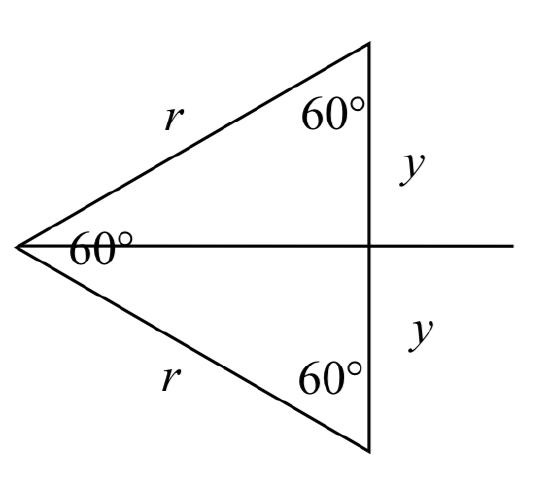 vertical line has length \(2y\), and since the sides are all equal we can conclude that \(2y = r\), or \(y=\dfrac{r}{2}\). Using this, we can find the sine value:
vertical line has length \(2y\), and since the sides are all equal we can conclude that \(2y = r\), or \(y=\dfrac{r}{2}\). Using this, we can find the sine value:
\[\text{sin}(\dfrac{\pi}{6}) = \dfrac{y}{r} = \dfrac{r/2}{r} = \dfrac{r}{2} \cdot \dfrac{1}{r} = \dfrac{1}{2}\nonumber\]
Using the Pythagorean Identity, we can find the cosine value:
\[\cos ^{2} \left(\dfrac{\pi }{6} \right)+\sin ^{2} \left(\dfrac{\pi }{6} \right)=1\nonumber\]
\[\cos ^{2} \left(\dfrac{\pi }{6} \right)+\left(\dfrac{1}{2} \right)^{2} =1\nonumber\]
\[\cos ^{2} \left(\dfrac{\pi }{6} \right)=\dfrac{3}{4}\nonumber\] since the \(x\) value is positive, we’ll keep the positive root
\[\cos \left(\dfrac{\pi }{6} \right)=\sqrt{\dfrac{3}{4} } =\dfrac{\sqrt{3} }{2}\nonumber\]
The (\(x\), \(y\)) coordinates for the point on a circle of radius 1 at an angle of 30 degrees are \(\left(\dfrac{\sqrt{3} }{2} ,\dfrac{1}{2} \right)\).
By drawing a the triangle inside the unit circle with a 30 degree angle and reflecting it over the line \(y = x\), we can find the cosine and sine for 60 degrees, or \(\dfrac{\pi }{3}\), without any additional work.
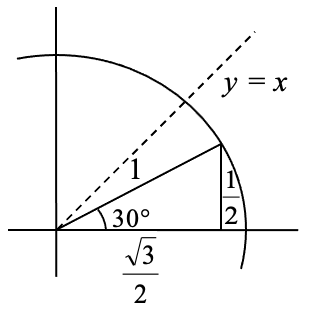
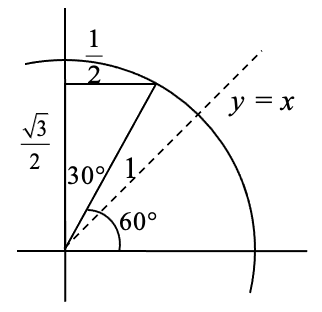
By this symmetry, we can see the coordinates of the point on the unit circle at an angle of 60 degrees will be \(\left(\dfrac{1}{2} ,\dfrac{\sqrt{3} }{2} \right)\), giving
\(\cos \left(\dfrac{\pi }{3} \right)=\dfrac{1}{2}\) and \(\sin \left(\dfrac{\pi }{3} \right)=\dfrac{\sqrt{3} }{2}\)
We have now found the cosine and sine values for all the commonly encountered angles in the first quadrant of the unit circle.
| Angle |
\(0\) |
\(\dfrac{\pi }{6}\), or 30\(\mathrm{{}^\circ}\) |
\(\dfrac{\pi }{4}\), or 45\(\mathrm{{}^\circ}\) |
\(\dfrac{\pi }{3}\), or 60\(\mathrm{{}^\circ}\) |
\(\dfrac{\pi }{2}\), or 90\(\mathrm{{}^\circ}\) |
| Cosine |
1 |
\(\dfrac{\sqrt{3} }{2}\) |
\(\dfrac{\sqrt{2} }{2}\) |
\(\dfrac{1}{2}\) |
0 |
| Sine |
0 |
\(\dfrac{1}{2}\) |
\(\dfrac{\sqrt{2} }{2}\) |
\(\dfrac{\sqrt{3} }{2}\) |
1 |
For any given angle in the first quadrant, there will be an angle in another quadrant with the same sine value, and yet another angle in yet another quadrant with the same cosine value. Since the sine value is the \(y\) coordinate on the unit circle, the other angle with the same sine will share the same \(y\) value, but have the opposite \(x\) value. Likewise, the angle with the same cosine will share the same \(x\) value, but have the opposite \(y\) value.
As shown here, angle \(\alpha\) has the same sine value as angle \(\theta\); the cosine values would be opposites. The angle \(\beta\) has the same cosine value as the angle \(\theta\); the sine values would be opposites.
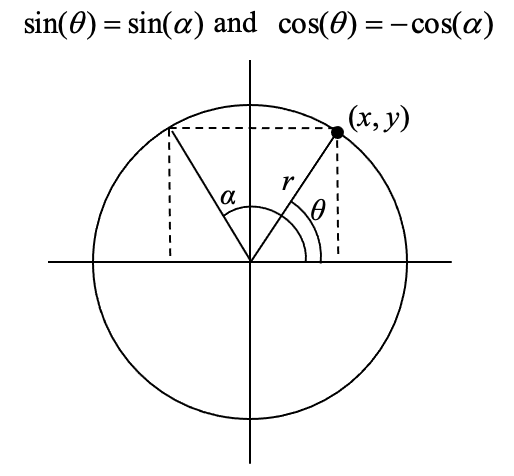
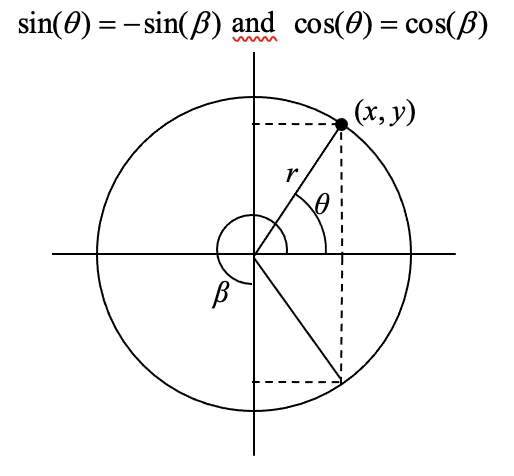
It is important to notice the relationship between the angles. If, from the angle, you measured the smallest angle to the horizontal axis, all would have the same measure in absolute value. We say that all these angles have a reference angle of \(\theta\).
Definition: reference angle
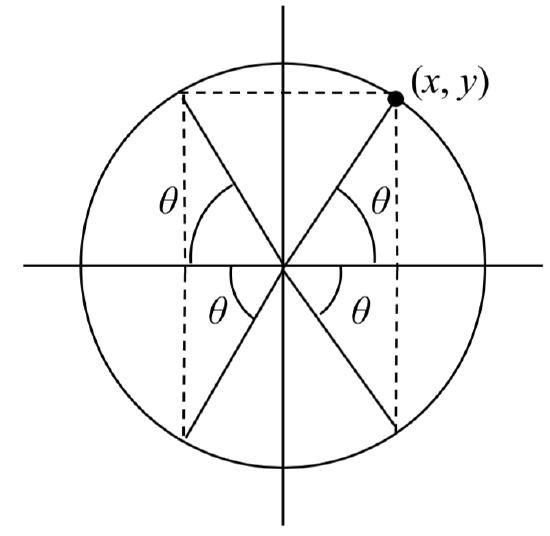 An angle’s reference angle is the size of the smallest angle to the horizontal axis.
An angle’s reference angle is the size of the smallest angle to the horizontal axis.
A reference angle is always an angle between 0 and 90 degrees, or 0 and \(\dfrac{\pi }{2}\) radians.
Angles share the same cosine and sine values as their reference angles, except for signs (positive or negative) which can be determined from the quadrant of the angle.
Example \(\PageIndex{5}\)
Find the reference angle of 150 degrees. Use it to find \(\cos (150{}^\circ )\) and \(\sin (150{}^\circ )\).
Solution
150 degrees is located in the second quadrant. It is 30 degrees short of the horizontal axis at 180 degrees, so the reference angle is 30 degrees.
This tells us that 150 degrees has the same sine and cosine values as 30 degrees, except for sign. We know that \(\sin (30{}^\circ )=\dfrac{1}{2}\) and \(\cos (30{}^\circ )=\dfrac{\sqrt{3} }{2}\). Since 150 degrees is in the second quadrant, the \(x\) coordinate of the point on the circle would be negative, so the cosine value will be negative. The \(y\) coordinate is positive, so the sine value will be positive.
\[\sin (150{}^\circ )=\dfrac{1}{2}\text{ and }\cos (150{}^\circ )=-\dfrac{\sqrt{3} }{2}\nonumber\]
The (\(x\), \(y\)) coordinates for the point on a unit circle at an angle of \(150{}^\circ\) are \(\left(\dfrac{-\sqrt{3} }{2} ,\dfrac{1}{2} \right)\).
Using symmetry and reference angles, we can fill in cosine and sine values at the rest of the special angles on the unit circle. Take time to learn the (\(x\), \(y\)) coordinates of all the major angles in the first quadrant!
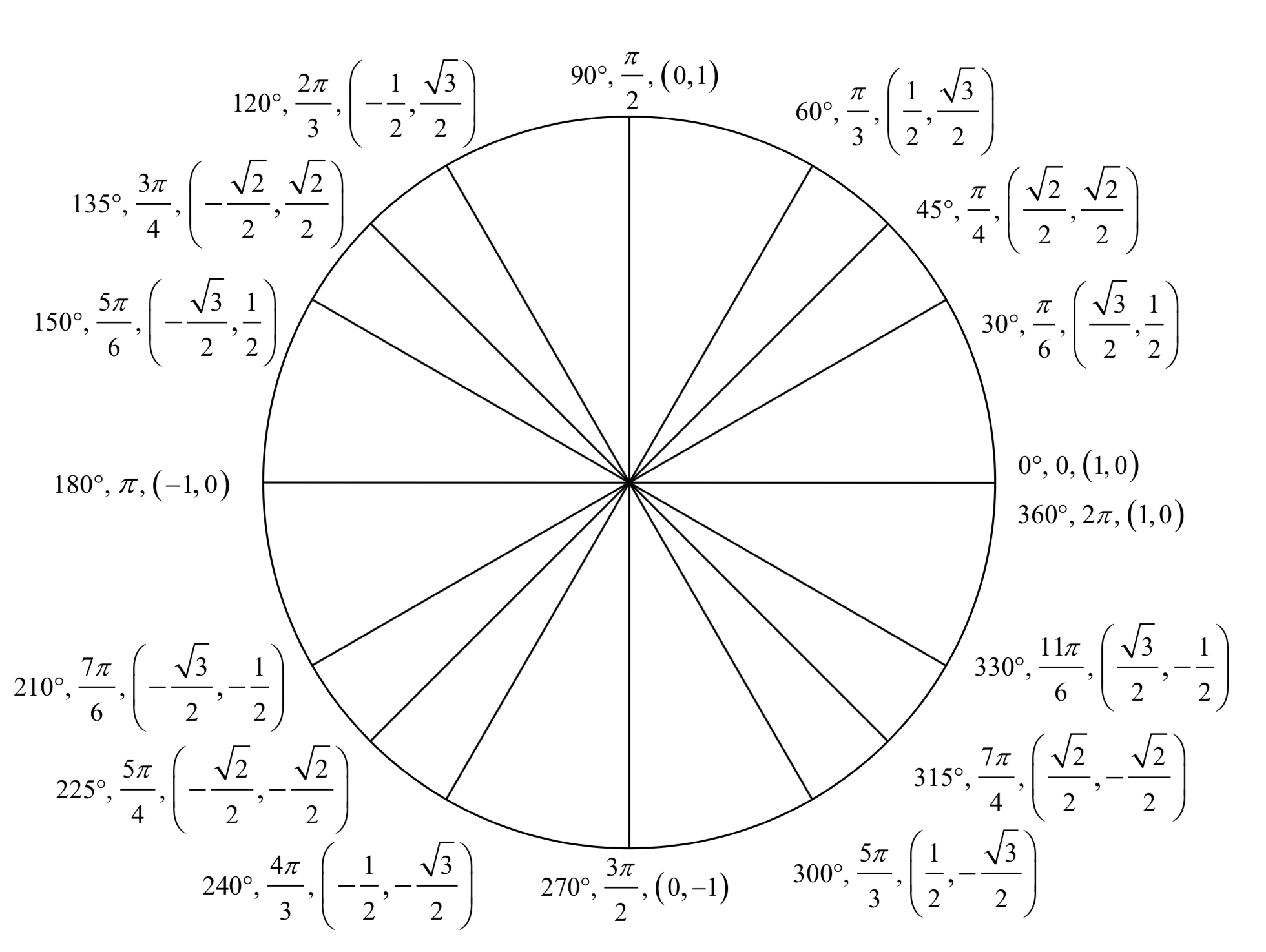
Example \(\PageIndex{6}\)
Find the coordinates of the point on a circle of radius 12 at an angle of \(\dfrac{7\pi }{6}\).
Solution
Note that this angle is in the third quadrant, where both x and y are negative. Keeping this in mind can help you check your signs of the sine and cosine function.
\[x=12\cos \left(\dfrac{7\pi }{6} \right)=12\left(\dfrac{-\sqrt{3} }{2} \right)=-6\sqrt{3}\nonumber \] \[y=12\sin \left(\dfrac{7\pi }{6} \right)=12\left(\dfrac{-1}{2} \right)=-6\nonumber\]
The coordinates of the point are \((-6\sqrt{3} ,-6)\).
Exercise \(\PageIndex{3}\)
Find the coordinates of the point on a circle of radius 5 at an angle of \(\dfrac{5\pi }{3}\).
- Answer
-
\[\left(5\cos \left(\dfrac{5\pi }{3} \right),5\sin \left(\dfrac{5\pi }{3} \right)\right)=\left(\dfrac{5}{2} ,\dfrac{-5\sqrt{3} }{2} \right)\nonumber\]
Example \(\PageIndex{7}\)
We now have the tools to return to the sailboat question posed at the beginning of this section.
Solution
A distress signal is sent from a sailboat during a storm, but the transmission is unclear and the rescue 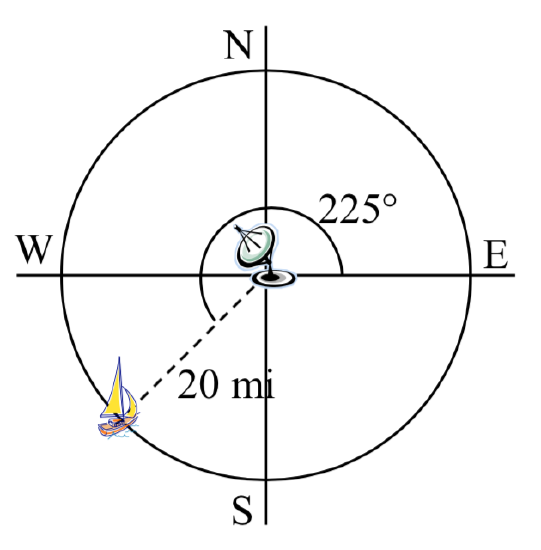 boat sitting at the marina cannot determine the sailboat’s location. Using high powered radar, they determine the distress signal is coming from a point 20 miles away at an angle of 225 degrees from the marina. How many miles east/west and north/south of the rescue boat is the stranded sailboat?
boat sitting at the marina cannot determine the sailboat’s location. Using high powered radar, they determine the distress signal is coming from a point 20 miles away at an angle of 225 degrees from the marina. How many miles east/west and north/south of the rescue boat is the stranded sailboat?
We can now answer the question by finding the coordinates of the point on a circle with a radius of 20 miles at an angle of 225 degrees.
\[x=20\cos \left(225{}^\circ \right)=20\left(\dfrac{-\sqrt{2} }{2} \right)\approx -14.142\text{ miles}\nonumber\]
\[y=20\sin \left(225{}^\circ \right)=20\left(\dfrac{-\sqrt{2} }{2} \right)\approx -14.142\text{ miles}\nonumber\]
The sailboat is located 14.142 miles west and 14.142 miles south of the marina.
The special values of sine and cosine in the first quadrant are very useful to know, since knowing them allows you to quickly evaluate the sine and cosine of very common angles without needing to look at a reference or use your calculator. However, scenarios do come up where we need to know the sine and cosine of other angles.
To find the cosine and sine of any other angle, we turn to a computer or calculator. Be aware: most calculators can be set into “degree” or “radian” mode, which tells the calculator the units for the input value. When you evaluate “cos(30)” on your calculator, it will evaluate it as the cosine of 30 degrees if the calculator is in degree mode, or the cosine of 30 radians if the calculator is in radian mode. Most computer software with cosine and sine functions only operates in radian mode.
Example \(\PageIndex{8}\)
Evaluate the cosine of 20 degrees using a calculator or computer.
Solution
On a calculator that can be put in degree mode, you can evaluate this directly to be approximately 0.939693.
On a computer or calculator without degree mode, you would first need to convert the angle to radians, or equivalently evaluate the expression \[\cos \left(20 \cdot \dfrac{\pi }{180} \right)\nonumber\]
Important Topics of This Section
- The sine function
- The cosine function
- Pythagorean Identity
- Unit Circle values
- Reference angles
- Using technology to find points on a circle



 , and marking the point on the circle indicated by some angle \(\theta\). This point has coordinates (\(x\), \(y\)).
, and marking the point on the circle indicated by some angle \(\theta\). This point has coordinates (\(x\), \(y\)).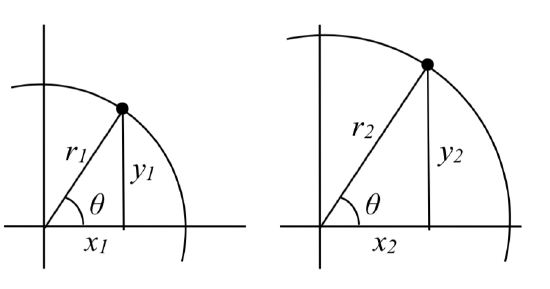
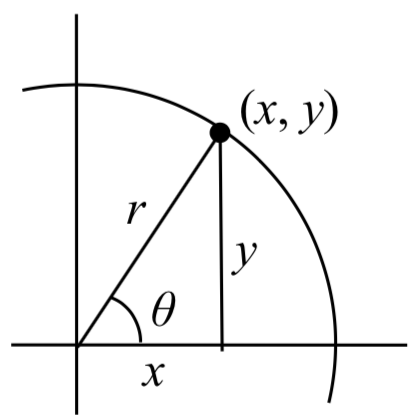 For the point (\(x\), \(y\)) on a circle of radius \(r\) at an angle of \(\theta\), we can define two important functions as the ratios of the sides of the corresponding triangle:
For the point (\(x\), \(y\)) on a circle of radius \(r\) at an angle of \(\theta\), we can define two important functions as the ratios of the sides of the corresponding triangle:
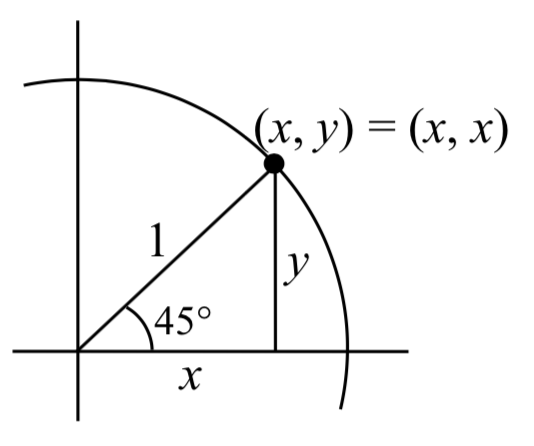 grees, or \(\dfrac{\pi }{4}\). At this angle, the x and y coordinates of the corresponding point on the circle will be equal because 45 degrees divides the first quadrant in half. Since the \(x\) and \(y\) values will be the same, the sine and cosine values will also be equal. Utilizing the Pythagorean Identity,
grees, or \(\dfrac{\pi }{4}\). At this angle, the x and y coordinates of the corresponding point on the circle will be equal because 45 degrees divides the first quadrant in half. Since the \(x\) and \(y\) values will be the same, the sine and cosine values will also be equal. Utilizing the Pythagorean Identity, . To do this, we will first draw a triangle inside a circle with one side at an angle of 30 degrees, and another at an angle of -30 degrees. If the resulting two right triangles are combined into one large triangle, notice that all three angles of this larger triangle will be 60 degrees.
. To do this, we will first draw a triangle inside a circle with one side at an angle of 30 degrees, and another at an angle of -30 degrees. If the resulting two right triangles are combined into one large triangle, notice that all three angles of this larger triangle will be 60 degrees. vertical line has length \(2y\), and since the sides are all equal we can conclude that \(2y = r\), or \(y=\dfrac{r}{2}\). Using this, we can find the sine value:
vertical line has length \(2y\), and since the sides are all equal we can conclude that \(2y = r\), or \(y=\dfrac{r}{2}\). Using this, we can find the sine value:

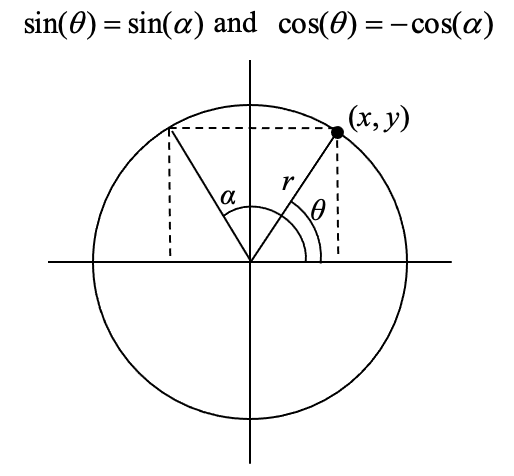
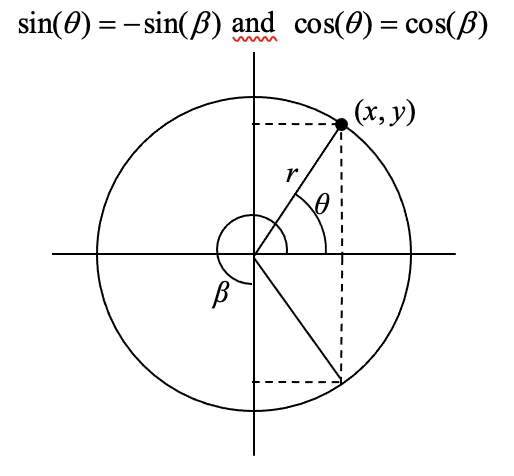
 An angle’s reference angle is the size of the smallest angle to the horizontal axis.
An angle’s reference angle is the size of the smallest angle to the horizontal axis.
 boat sitting at the marina cannot determine the sailboat’s location. Using high powered radar, they determine the distress signal is coming from a point 20 miles away at an angle of 225 degrees from the marina. How many miles east/west and north/south of the rescue boat is the stranded sailboat?
boat sitting at the marina cannot determine the sailboat’s location. Using high powered radar, they determine the distress signal is coming from a point 20 miles away at an angle of 225 degrees from the marina. How many miles east/west and north/south of the rescue boat is the stranded sailboat?