5.8: Solving Trigonometric Equations

In Section 6.1, we determined the height of a rider on the London Eye Ferris wheel could be determined by the equation

$$h(t)=-65\cos \left(\dfrac{\pi }{15} t\right)+70. \nonumber$$

If we wanted to know length of time during which the rider is more than 100 meters above ground, we would need to solve equations involving trig functions.

Solving using Known Values

In the last chapter, we learned sine and cosine values at commonly encountered angles. We can use these to solve sine and cosine equations involving these common angles.

Example $\PageIndex{1}$

Solve $\sin \left(t\right)=\dfrac{1}{2}$ for all possible values of $t$.

Solution

Notice this is asking us to identify all angles, $t$, that have a sine value of $\dfrac{1}{2}$. While evaluating a function always produces one result, solving for an input can yield multiple solutions. Two solutions should immediately jump to mind from the last chapter: $t=\dfrac{\pi }{6}$ and $t=\dfrac{5\pi }{6}$ because they are the common angles on the unit circle with a sin of $\dfrac{1}{2}$.

Looking at a graph confirms that there are more than these two solutions. While eight are seen on this graph, there are an infinite number of solutions!

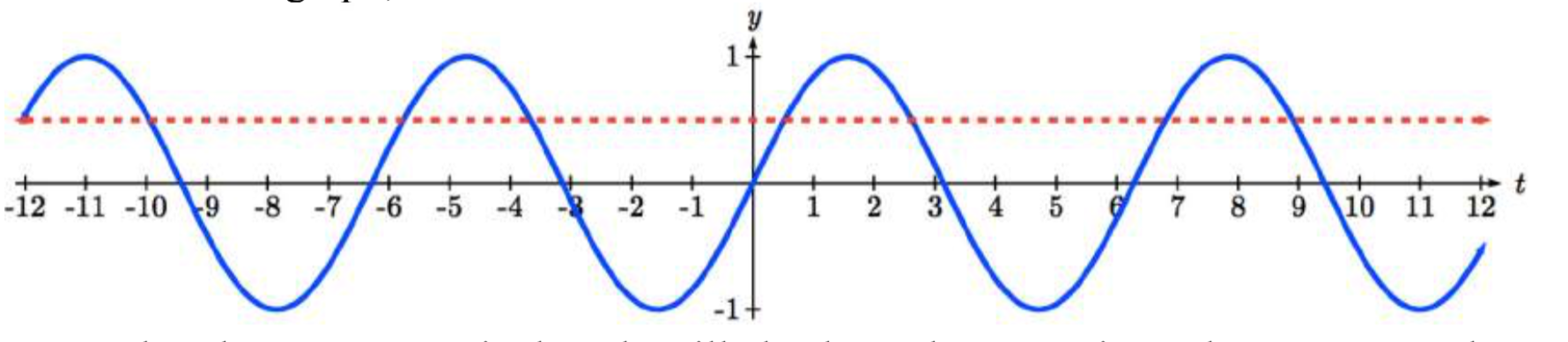
Remember that any coterminal angle will also have the same sine value, so any angle coterminal with these our first two solutions is also a solution. Coterminal angles can be found by adding full rotations of 2$\pi$, so we can write the full set of solutions:

$t=\dfrac{\pi }{6} +2\pi k$ where k is an integer, and $t=\dfrac{5\pi }{6} +2\pi k$ where $k$ is an integer.

Example $\PageIndex{2}$

A circle of radius $5\sqrt{2}$ intersects the line $x = -5$ at two points. Find the angles $\theta$ on the interval $0 \le \theta <2\pi$, where the circle and line intersect.

Solution

The $x$ coordinate of a point on a circle can be found as $x=r\cos \left(\theta \right)$, so the $x$ coordinate of points on this circle would be $x=5\sqrt{2} \cos \left(\theta \right)$. To find where the line $x = -5$ intersects the circle, we can solve for where the $x$ value on the circle would be -5.

$$-5=5\sqrt{2} \cos \left(\theta \right)\nonumber$$Isolating the cosine

$$\dfrac{-1}{\sqrt{2} } =\cos \left(\theta \right)\nonumber$$ Recall that $\dfrac{-1}{\sqrt{2} } =\dfrac{-\sqrt{2} }{2}$, so we are solving

$$\cos \left(\theta \right)=\dfrac{-\sqrt{2} }{2}\nonumber$$

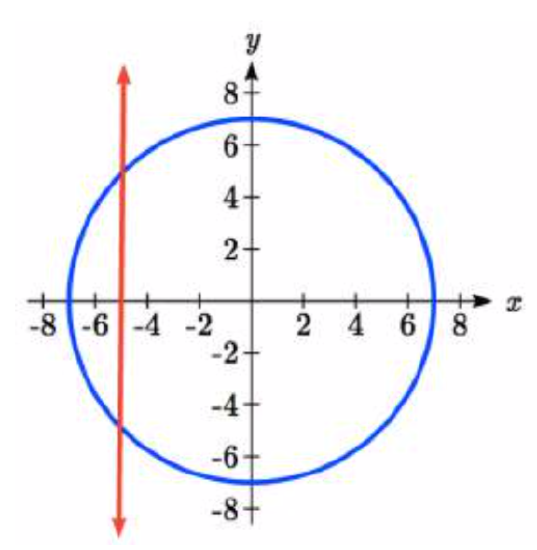
We can recognize this as one of our special cosine values from our unit circle, and it corresponds with angles $$\theta =\dfrac{3\pi }{4}\text{ and }\theta =\dfrac{5\pi }{4}\nonumber$$

Exercise $\PageIndex{1}$

Solve $\tan \left(t\right)=1$ for all possible values of $t$.

Answer

From our special angles, we know one answer is $t=\dfrac{\pi }{4}$. Tangent equations only have one unique solution per cycle or period, so additional solutions can be found by adding multiples of a full period, $\pi$. $$t=\dfrac{\pi }{4} +\pi k\nonumber$$

Example $\PageIndex{3}$

The depth of water at a dock rises and falls with the tide, following the equation $f(t)=4\sin \left(\dfrac{\pi }{12} t\right)+7$, where t is measured in hours after midnight. A boat requires a depth of 9 feet to tie up at the dock. Between what times will the depth be 9 feet?

Solution

To find when the depth is 9 feet, we need to solve $f(t) = 9$.

$$4\sin \left(\dfrac{\pi }{12} t\right)+7=9\nonumber$$Isolating the sine
$$4\sin \left(\dfrac{\pi }{12} t\right)=2\nonumber$$Dividing by $4$
$$\sin \left(\dfrac{\pi }{12} t\right)=\dfrac{1}{2}\nonumber$$We know $\sin \left(\theta \right)=\dfrac{1}{2}$ when $\theta =\dfrac{\pi }{6} \quad or\quad \theta =\dfrac{5\pi }{6}$

While we know what angles have a sine value of $\dfrac{1}{2}$, because of the horizontal stretch/compression it is less clear how to proceed.

To deal with this, we can make a substitution, defining a new temporary variable $u$ to be $u=\dfrac{\pi }{12} t$, so our equation $\sin \left(\dfrac{\pi }{12} t\right)=\dfrac{1}{2}$ becomes

$$\sin \left(u\right)=\dfrac{1}{2}\nonumber$$

From earlier, we saw the solutions to this equation were

$$u=\dfrac{\pi }{6} +2\pi k\nonumber$$where $k$ is an integer, and
$$u=\dfrac{5\pi }{6} +2\pi k\nonumber$$where k is an integer

To undo our substitution, we replace the $u$ in the solutions with $u=\dfrac{\pi }{12} t$ and solve for $t$.

$\dfrac{\pi }{12} t=\dfrac{\pi }{6} +2\pi k$ where $k$ is an integer, and $\dfrac{\pi }{12} t=\dfrac{5\pi }{6} +2\pi k$ where $k$ is an integer.

Dividing by 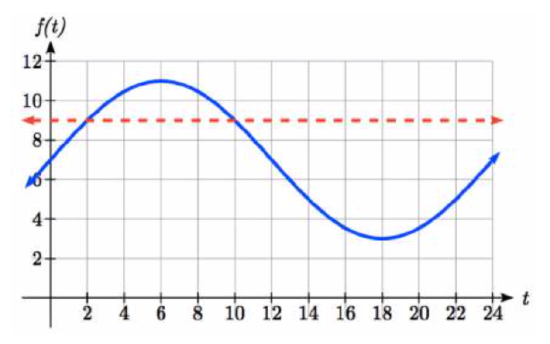$\pi$/12, we obtain solutions

$t=2+24k$ where $k$ is an integer, and $t=10+24k$ where $k$ is an integer.

The depth will be 9 feet and the boat will be able to approach the dock between 2 am and 10 am.

Notice how in both scenarios, the 24k shows how every 24 hours the cycle will be repeated.

In the previous example, looking back at the original simplified equation $\sin \left(\dfrac{\pi }{12} t\right)=\dfrac{1}{2}$, we can use the ratio of the “normal period” to the stretch factor to find the period: $\dfrac{2\pi }{\left(\dfrac{\pi }{12} \right)} =2\pi \left(\dfrac{12}{\pi } \right)=24$. Notice that the sine function has a period of 24, which is reflected in the solutions: there were two unique solutions on one full cycle of the sine function, and additional solutions were found by adding multiples of a full period.

Exercise $\PageIndex{2}$

Solve $4\sin (5t)-1=1$ for all possible values of $t$.

Answer

$$4\sin (5t)-1=1\nonumber$$

$$\sin (5t)=\dfrac{1}{2}\nonumber$$ Let $u=5t$ so this becomes $\sin (u)=\dfrac{1}{2}$, which has solutions

$$u=\dfrac{\pi }{6} +2\pi k,\dfrac{5\pi }{6} +2\pi k\nonumber$$Solving $$5t=u=\dfrac{\pi }{6} +2\pi k,\dfrac{5\pi }{6} +2\pi k\nonumber$$ gives the solutions

$$t=\dfrac{\pi }{30} +\dfrac{2\pi }{5} k\qquad t=\dfrac{\pi }{6} +\dfrac{2\pi }{5} k\nonumber$$

Solving using the Inverse Trig Functions

Not all equations involve the “special” values of the trig functions to we have learned. To find the solutions to these equations, we need to use the inverse trig functions.

Example $\PageIndex{4}$

Use the inverse sine function to find one solution to $\sin \left(\theta \right)=0.8$.

Solution

Since this is not a known unit circle value, calculating the inverse, $\theta =\sin ^{-1} \left(0.8\right)$. This requires a calculator and we must approximate a value for this angle. If your calculator is in degree mode, your calculator will give you an angle in degrees as the output. If your calculator is in radian mode, your calculator will give you an angle in radians. In radians, $\theta =\sin ^{-1} \left(0.8\right)\approx 0.927$, or in degrees, $\theta =\sin ^{-1} \left(0.8\right)\approx 53.130{}^\circ$.

If you are working with a composed trig function and you are not solving for an angle, you will want to ensure that you are working in radians. In calculus, we will almost always want to work with radians since they are unit-less.

Notice that the inverse trig functions do exactly what you would expect of any function – for each input they give exactly one output. While this is necessary for these to be a function, it means that to find all the solutions to an equation like $\sin \left(\theta \right)=0.8$, we need to do more than just evaluate the inverse function.

To find additional solutions, it is good to remember four things:

• The sine is the $y$-value of a point on the unit circle
• The cosine is the $x$-value of a point on the unit circle
• The tangent is the slope of a line at a given angle
• Other angles with the same $\sin$/$\cos$/$\tan$ will have the same reference angle

Example $\PageIndex{5}$

Find all solutions to $\sin \left(\theta \right)=0.8$.

Solution

We would expect two unique angles on one cycle to have this sine value. In the previous example, we found one solution to be 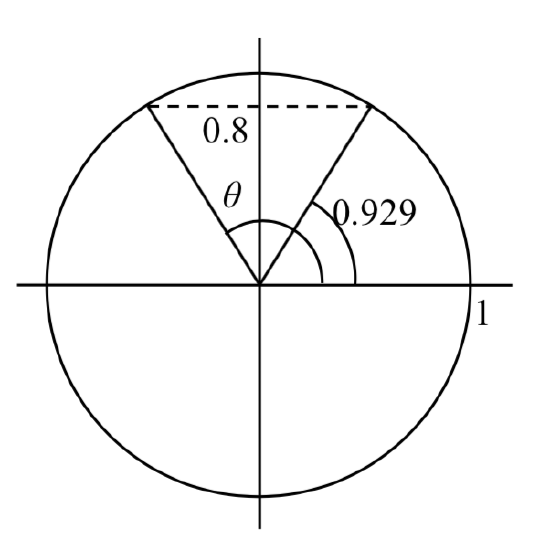$\theta =\sin ^{-1} \left(0.8\right)\approx 0.927$. To find the other, we need to answer the question “what other angle has the same sine value as an angle of 0.927?”

We can think of this as finding all the angles where the y-value on the unit circle is 0.8. Drawing a picture of the circle helps how the symmetry.

On a unit circle, we would recognize that the second angle would have the same reference angle and reside in the second quadrant. This second angle would be located at $\theta =\pi -\sin ^{-1} (0.8)$, or approximately $\theta \approx \pi -0.927=2.214$.

To find more solutions we recall that angles coterminal with these two would have the same sine value, so we can add full cycles of 2$\pi$.

$$\theta =\sin ^{-1} (0.8) +2\pi k\nonumber$$ and $$\theta =\pi -\sin ^{-1} (0.8)+2\pi k\nonumber$$ where $k$ is an integer,
or approximately, $\theta =0.927+2\pi k$ and $\theta =2.214+2\pi k$ where $k$ is an integer.

Example $\PageIndex{6}$

Find all solutions to $\sin \left(x\right)=-\dfrac{8}{9}$ on the interval $0{}^\circ \le x<360{}^\circ$.

Solution

We are looking for the angles with a 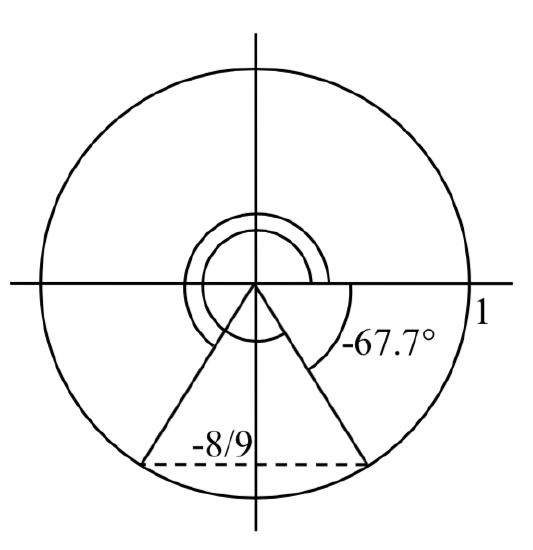$y$-value of -8/9 on the unit circle. Immediately we can see the solutions will be in the third and fourth quadrants.

First, we will turn our calculator to degree mode. Using the inverse, we can find one solution $x=\sin ^{-1} \left(-\dfrac{8}{9} \right)\approx -62.734{}^\circ$. While this angle satisfies the equation, it does not lie in the domain we are looking for. To find the angles in the desired domain, we start looking for additional solutions.

First, an angle coterminal with $-62.734{}^\circ$will have the same sine. By adding a full rotation, we can find an angle in the desired domain with the same sine.

$$x=-62.734{}^\circ +360{}^\circ =297.266{}^\circ\nonumber$$

There is a second angle in the desired domain that lies in the third quadrant. Notice that $62.734{}^\circ$ is the reference angle for all solutions, so this second solution would be $62.734{}^\circ$ past $180{}^\circ$

$$x=62.734{}^\circ +180{}^\circ =242.734{}^\circ\nonumber$$

The two solutions on $0{}^\circ \le x<360{}^\circ$ are $x$ = $297.266{}^\circ$ and $x$ = $242.734{}^\circ$

Example $\PageIndex{7}$

Find all solutions to $\tan \left(x\right)=3$ on $0 \le x<2\pi$.

Solution

Using the inverse tangent function, we can find one solution 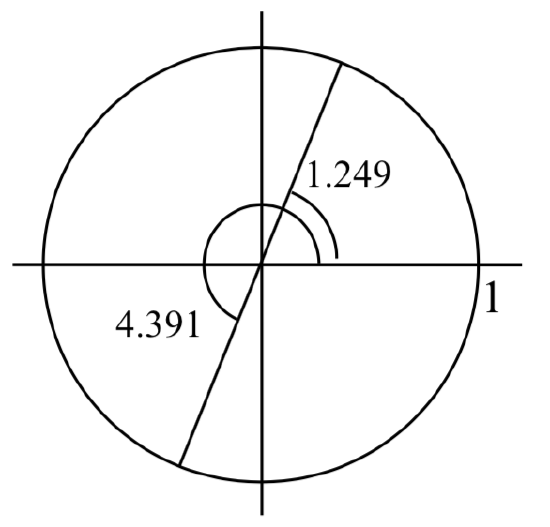$x=\tan ^{-1} \left(3\right) \approx 1.249$. Unlike the sine and cosine, the tangent function only attains any output value once per cycle, so there is no second solution in any one cycle.

By adding $\pi$, a full period of tangent function, we can find a second angle with the same tangent value. Notice this gives another angle where the line has the same slope.

If additional solutions were desired, we could continue to add multiples of $\pi$, so all solutions would take on the form $x=1.249+k\pi$, however we are only interested in $0 \le x< 2\pi$.

$$x=1.249+\pi =4.391\nonumber$$

The two solutions on $0\le x<2\pi$ are $x = 1.249$ and $x = 4.391$.

Exercise $\PageIndex{3}$

Find all solutions to $\tan \left(x\right)=0.7$ on $0{}^\circ \le x<360{}^\circ$.

Answer

The first solution is $x=\tan ^{-1} (0.7) \approx 34.992{}^\circ$.

For a standard tangent, the second solution can be found by adding a full period, $180\mathrm{{}^\circ}$, giving $$x=180{}^\circ +34.99{}^\circ =214.992{}^\circ\nonumber$$

Example $\PageIndex{8}$

Solve $3\cos \left(t\right)+4=2$ for all solutions on one cycle, $0\le t<2\pi$

Solution

$$3\cos \left(t\right)+4=2\nonumber$$Isolating the cosine
$$3\cos \left(t\right)=-2\nonumber$$
$$\cos \left(t\right)=-\dfrac{2}{3}\nonumber$$Using the inverse, we can find one solution
$$t=\cos ^{-1} \left(-\dfrac{2}{3} \right)\approx 2.301\nonumber$$

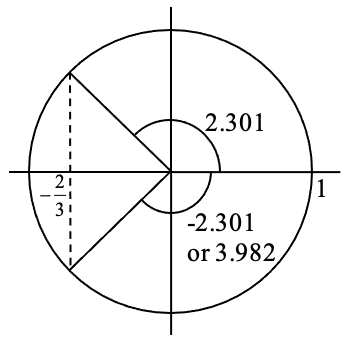
We’re looking for two angles where the $x$-coordinate on a unit circle is -2/3. A second angle with the same cosine would be located in the third quadrant. Notice that the location of this angle could be represented as $t=-2.301$. To represent this as a positive angle we could find a coterminal angle by adding a full cycle.

$$t=-2.301+2\pi = 3.982\nonumber$$

The equation has two solutions between 0 and 2$\pi$, at $t = 2.301$ and $t = 3.982$.

Example $\PageIndex{9}$

Solve $\cos \left(3t\right)=0.2$ for all solutions on two cycles, $0\le t<\dfrac{4\pi }{3}$.

Solution

As before, with a horizontal compression it can be helpful to make a substitution, $u=3t$ Making this substitution simplifies the equation to a form we have already solved.

$$\cos \left(u\right)=0.2\nonumber$$
$$u=\cos ^{-1} \left(0.2\right)\approx 1.369\nonumber$$

A second solution on one cycle would be located in the fourth quadrant with the same reference angle.

$$u=2\pi -1.369=4.914\nonumber$$

In this case, we need all solutions on two cycles, so we need to find the solutions on the second cycle. We can do this by adding a full rotation to the previous two solutions.

$$\begin{array}{l} {u=1.369+2\pi =7.653} \\ {u=4.914+2\pi =11.197} \end{array}\nonumber$$

Undoing the substitution, we obtain our four solutions:

$$3t = 1.369\text{, so }t = 0.456\nonumber$$
$$3t = 4.914\text{, so }t = 1.638\nonumber$$
$$3t = 7.653\text{, so }t = 2.551\nonumber$$
$$3t = 11.197\text{, so }t = 3.732\nonumber$$

Example $\PageIndex{10}$

Solve $3\sin \left(\pi \, t\right)=-2$ for all solutions.

Solution

$$3\sin \left(\pi \, t\right)=-2\nonumber$$Isolating the sine

$$\sin \left(\pi \, t\right)=-\dfrac{2}{3}\nonumber$$We make the substitution $u=\pi \, t$

$$\sin \left(u\right)=-\dfrac{2}{3}\nonumber$$Using the inverse, we find one solution

$$u=\sin ^{-1} \left(-\dfrac{2}{3} \right)\approx -0.730\nonumber$$

This angle is in the fourth quadrant. A second angle with the same sine would be in the third quadrant with 0.730 as a reference angle:

$$u=\pi +0.730=3.871\nonumber$$

We can write all solutions to the equation $\sin \left(u\right)=-\dfrac{2}{3}$ as

$$u=-0.730+2\pi {\kern 1pt} k\text{ or }u=3.871+2\pi {\kern 1pt} k\nonumber$$where $k$ is an integer.

Undoing our substitution, we can replace u in our solutions with $u=\pi \, t$ and solve for $t$

$$\pi t=-0.730+2\pi k\text{ or }\pi t=3.871+2\pi k\nonumber$$

Divide by $\pi$
$$t=-0.232+2 k\text{ or } t=1.232+2 k\nonumber$$

Exercise $\PageIndex{4}$

Solve $5\sin \left(\dfrac{\pi }{2} t\right)+3=0$ for all solutions on one cycle, $0 \le t < 4$.

Answer

$$\sin \left(\dfrac{\pi }{2} t\right)=-\dfrac{3}{5}\nonumber$$Let $u=\dfrac{\pi }{2} t$, so this becomes $$\sin \left(u\right)=-\dfrac{3}{5}\nonumber$$

Using the inverse, $u=\sin ^{-1} \left(-\dfrac{3}{5} \right)\approx -0.6435$. Since we want positive solutions, we can find the coterminal solution by adding a full cycle: $u=-0.6435+2\pi =5.6397$. Another angle with the same sin would be in the third quadrant with the reference angle 0.6435. $u=\pi +0.6435=3.7851$.

Solving for $t$, $$u=\dfrac{\pi }{2} t=5.6397\nonumber$$, so $$t=5.6397\left(\dfrac{2}{\pi } \right)=3.5903\nonumber$$
and $$u=\dfrac{\pi }{2} t=3.7851\nonumber$$, so $$t=3.7851\left(\dfrac{2}{\pi } \right)=2.4097\nonumber$$
$$t = 2.4097\text{ or }t = 3.5903\nonumber$$

SOLVING TRIG EQUATIONS TRIGONOMETRY: SINUSOIDAL FUNCTIONS

1. Isolate the trig function on one side of the equation
2. Make a substitution for the inside of the sine, cosine, or tangent (or other trig function)
3. Use inverse trig functions to find one solution
4. Use symmetries to find a second solution on one cycle (when a second exists)
5. Find additional solutions if needed by adding full periods
6. Undo the substitution

We now can return to the question we began the section with.

Example $\PageIndex{11}$

The height of a rider on the London Eye Ferris wheel can be determined by the equation $h(t)=-65\cos \left(\dfrac{\pi }{15} t\right)+70$. How long is the rider more than 100 meters above ground?

Solution

To find how long the rider is above 100 meters, we first find the times at which the rider is at a height of 100 meters by solving h(t) = 100.

$$100=-65\cos \left(\dfrac{\pi }{15} t\right)+70\nonumber$$Isolating the cosine
$$30=-65\cos \left(\dfrac{\pi }{15} t\right)\nonumber$$
$$\dfrac{30}{-65} =\cos \left(\dfrac{\pi }{15} t\right)\nonumber$$We make the substitution $u=\dfrac{\pi }{15} t$
$$\dfrac{30}{-65} =\cos (u)\nonumber$$Using the inverse, we find one solution
$$u=\cos ^{-1} \left(\dfrac{30}{-65} \right)\approx 2.051\nonumber$$

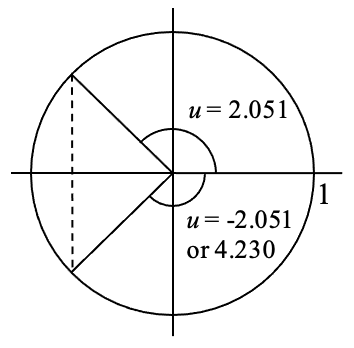
This angle is in the second quadrant. A second angle with the same cosine would be symmetric in the third quadrant. This angle could be represented as u = -2.051, but we need a coterminal positive angle, so we add 2$\pi$:

$$u=2\pi -2.051\approx 4.230\nonumber$$

Now we can undo the substitution to solve for $t$

$\dfrac{\pi }{15} t=2.051$ so $t = 9.793$ minutes after the start of the ride
$\dfrac{\pi }{15} t=4.230$ so $t = 20.197$ minutes after the start of the ride

A rider will be at 100 meters after 9.793 minutes, and again after 20.197 minutes. From the behavior of the height graph, we know the rider will be above 100 meters between these times. A rider will be above 100 meters for 20.197 - 9.793 = 10.404 minutes of the ride.

Important Topics of This Section

• Solving trig equations using known values
• Using substitution to solve equations
• Finding answers in one cycle or period vs. finding all possible solutions
• Method for solving trig equations