1.6: Work

Absolute Prerequisites

Prerequisite Topics

The following (prerequisite) topics related to the material in this section must be assumed to have already been mastered by the student. Due to time constraints and the basic level of the material, these topics will not be covered in this course (even if your class has corequisite support).

• Algebra
  • Unit analysis
• Trigonometry
  • All of Right Triangle Trigonometry

If you are consistently struggling with these skills, you would be better served taking MATH 384: Foundations for Calculus with a Corequisite Support course.

---

Learning Objectives

• Calculate the work done by a variable force acting along a line.
• Calculate the work done in lifting objects.
• Calculate the work done in pumping a liquid from one height to another.

---

In this section, we turn our attention to work. The concept of work is the backbone of many Physics problems, and we will investigate the energy expenditure in several increasingly complex situations.

Work Done by a Constant Force

Videos

• Defining Force
• Defining Work

You have likely read about Newton's Second Law of Motion, which states that force (which is often intuitively defined as a push or a pull on an object) is the product of an object's mass and its acceleration. That is, $$F = m a. \nonumber$$ For our current conversation, we will only consider the acceleration due to gravity, traditionally denoted $g$. Therefore, we replace $a$ with $g$ to get.¹ $$F = m g. \label{Force}$$ When a force moves an object, we say the force does work on the object. In other words, work can be thought of as the amount of energy it takes to move an object through a distance. According to Physics, work can be expressed as the product of force and distance. That is, $$W = F d. \label{BasicWork}$$ You would not be wrong to state that we could combine Equations $\ref{Force}$ and $\ref{BasicWork}$ to arrive at $$W = m g d; \label{ForceWork}$$ however, the choice to do our mathematics with Equation $\ref{BasicWork}$ or Equation $\ref{ForceWork}$ will depend on which measurement system we are given.

The Metric and U.S. Customary Systems

There are two measurement systems we deal with in science - the English system (also known as the U.S. Customary System) and the metric system (also known as the International System of Units, or the S.I. System). We work with both systems in this course. For simplicity, the following table gives the unit names in each system (the base unit for time in both systems is the second).

	Distance $d$	Mass $m$	Gravitational Constant (at sea level) $g$	Force $F = m g$	Work $W = F d$
English System	foot (ft)	slug	$\approx 32.2 \, \left( \frac{\text{ft}}{\text{s}^2} \right)$	pound $\left( \frac{\text{slug-ft}}{\text{s}^2} \right)$	foot-pound $\left( \text{ft} \cdot \text{lbs} \right)$
Metric System	meter (m)	kilogram (kg)	$\approx 9.8 \, \left( \frac{\text{m}}{\text{s}^2} \right)$	newton $\left( \frac{\text{kg m}}{\text{s}^2} \equiv \text{N} \right)$	joule $\left( \frac{\text{kg m}}{\text{s}^2} \cdot \text{m} = \text{N m} \right)$

In the English system, the unit of force is the pound and the unit of distance is the foot. Therefore, according to Equation $\ref{BasicWork}$, work is given in foot-pounds. It is incredibly rare in the English system to state the mass of an object - instead, the force the Earth is exerting on that object (which we call pounds) is typically given. Therefore, when asked to compute the work done in a scenario involving the English system, you will use Equation $\ref{BasicWork}$.

In the metric system, kilograms and meters are used. The unit of force is called the newton.² Hence, according Equation $\ref{BasicWork}$, work is given in newton-meters. Unlike the English system, the metric system has a special unit name for work - the joule. Therefore, you can use the terminology "joule" and "newton-meter" interchangeably. Another difference between the English and metric systems is that, in the metric system, you will often be given the object's mass. Therefore, when computing work in scenarios involving the metric system, you will use Equation $\ref{ForceWork}$.

Example $\PageIndex{1}$: The Work Required to Push a Lawn Mower

Suppose you are pushing a lawn mower along flat, even ground. The handle makes an angle of $60^{\circ}$ with the ground and you are pushing with a constant force of 40 lbs over a distance of 80 feet. Compute the amount of work done on the lawn mower over this distance.

Solution

Only the horizontal component of the force adds work to the mower in this situation (the vertical component is wasted by pushing the mower into the ground), so we first need to compute the horizontal force we are applying to the mower. Suppose the force of 40 lbs is along the handle. In that case, the horizontal component of the force is computed using some spectacular Right Triangle Trigonometry: $$F_h = F \cos(60^{\circ}) = (40 \text{ lbs})(0.5) = 20 \text{ lbs}. \nonumber$$ Hence, according to Equation $\ref{BasicWork}$, the work done on the mower over an 80-foot stretch of ground is $$W = F_h \cdot d = (20 \text{ lbs}) \cdot (80 \text{ feet}) = 160 \text{ ft-lbs}. \nonumber$$

Notice in Example $\PageIndex{1}$ that I said "the work done on the mower," not "the work we did." When moving the mower, we are imparting energy to the mower; however, the energy we are imparting to the mower might not be (and, in this case, is not) the same as the energy we are expending in the process of moving the mower. Part of the energy we are using is pushing downward (into the ground) as we move the mower. This energy is not imparted to the mower and is completely wasted in the entire process. The only way to counteract this waste is to either push the mower from closer to ground level or build a mower tall enough that we are pushing from chest level. The issue with the former is that we would have to crawl or lean over the entire time, and the issue with the latter is that we would have to push with more force because the mower would be larger.

Before diving into an example, we need to discuss the concept of density briefly. The volumetric density (referred to as density) of a three-dimensional object is its mass per unit volume. In some disciplines, this is also known as the object's specific mass. If we let $\rho$, $m$, and $V$ be the density, mass, and volume, respectively, then $$\rho = \dfrac{m}{V} \implies m = \rho V. \label{MassDensityVolume}$$

Caution: Tricky Wording

What most people refer to as "density" in the U.S. Customary System is the weight density (also referred to as the specific weight) of the object. That is, since density is mass per unit volume, the units for density in the U.S. Customary System are technically slugs per cubic foot; however, you would search far and wide before you found anyone stating that the density of water is approximately $1.9 \text{ slugs}/\text{ft}^3$. Most people, even in scientific circles, cite the density of water (at $32^{ \circ } \, F$ as approximately $62.4 \text{ lbs}/\text{ft}^3$.

This "loose" definition of density is scientifically inaccurate as the pound is a force and, therefore, the quantity being used is force per unit volume - not mass per unit volume. To avoid confusion, I use "weight density" when referring to force per unit volume. The Greek letter $\gamma$ (lowercase "gamma") is traditionally used when referring to the weight density of an object, so I will use that convention in this text as well.

In light of the Cautionary statement above, it's best to (re)summarize our current knowledge in a table.

	Distance $d$	Mass $m$	Gravitational Constant (at sea level) $g$	Force $F = mg$	Density $\rho = \frac{\text{m}}{\text{d}^3}$	Weight Density $\gamma = \rho\, g = \frac{\text{F}}{\text{d}^3}$
English System	foot (ft)	slug	$\approx 32.2 \, \left( \frac{\text{ft}}{\text{s}^2} \right)$	pound $\left( \frac{\text{slug-ft}}{\text{s}^2} \right)$	$\left( \frac{\text{slugs}}{\text{ft}^3} \right)$	$\left( \frac{\text{lbs}}{\text{ft}^3} \right)$
Metric System	meter (m)	kilogram (kg)	$\approx 9.8 \, \left( \frac{\text{m}}{\text{s}^2} \right)$	newton $\left( \frac{\text{kg m}}{\text{s}^2} \equiv \text{N} \right)$	$\left( \frac{\text{kg}}{\text{m}^3} \right)$	$\left( \frac{\text{N}}{{m}^3} \right)$

The equations in $\ref{MassDensityVolume}$ will become incredibly important as we move forward. It's best to get used to them now.

Example $\PageIndex{2}$: The Work Required to Lift a Bucket (Part 1)

A 5-liter bucket is filled with water. By itself, the bucket has a mass of 2 kg.³ How much work is done in lifting the bucket from the bottom of a 60-meter-deep well? (Water has a density of $\rho_{\text{w}} = 1000 \, \text{kg}/\text{m}^3$, where $1 \, \text{L} = 0.001 \, \text{m}^3$).

Solution

The total mass of the bucket, including water, is $$\begin{array}{rcl} m & = & m_{\text{b}} + m_{\text{w}} \\[16pt] & = & m_{\text{b}} + \rho_{\text{w}} \cdot V_{\text{w}} \\[16pt] & = & 2 \text{ kg} + 1 \dfrac{\text{kg}}{\cancel{\text{L}}} \cdot 5 \, \cancel{\text{L}} \\[16pt] & = & 7 \text{ kg} \\ \end{array} \nonumber$$ Hence, according to Equation $\ref{ForceWork}$, the work done in lifting the bucket is $$\begin{array}{rcl} W & = & m \cdot g \cdot d \\[16pt] & \approx & \left( 7 \, \text{kg} \right) \left( 9.8 \, \dfrac{\text{m}}{\text{s}^2} \right) \left( 60 \, \text{m} \right) \\[16pt] & = & 4116 \, \dfrac{\text{kg m}}{\text{s}^2} \cdot \text{m} \\[16pt] & = & 4116 \, \text{N-m} \\[16pt] & = & 4116 \, \text{J} \\ \end{array} \nonumber$$

The end of Example $\PageIndex{2}$ showcases a couple important "unit concepts." First, the newton is often denoted $N$, and the joule is often denoted $J$. Second, force in the metric system (which is measured in newtons) is $\frac{\text{kg m}}{\text{s}^2}$.

Work Done by a Variable Force

When we have a constant force, things are pretty easy. It is rare, however, for a force to be constant. For example, the work done to compress (or elongate) a spring varies depending on how far the spring has already been compressed (or stretched). We look at springs in more detail later in this section.

Suppose we have a variable force, $F(x)$, that moves an object in a positive direction along the $x$-axis from point $a$ to point $b$. To calculate the work done, we partition the interval $[a,b]$ and estimate the work done over each subinterval. So, for $i=0,1,2, \ldots ,n$, let $P=\{x_i\}$ be a regular partition of the interval $[a,b]$, and for $i=1,2, \ldots ,n$, choose an arbitrary point $x^∗_i \in [x_{i−1},x_i]$. To calculate the work done to move an object from point $x_{i−1}$ to point $x_i$, we assume the force is roughly constant over this short interval, and use $F(x^∗_i)$ to approximate the force used to move the object through this interval. The work done over the interval $[x_{i−1},x_i]$, then, is given by $$W_i \approx F(x^∗_i)(x_{i}−x_{i−1})=F(x^∗_i) \Delta x. \nonumber$$ Therefore, the work done over the interval $[a,b]$ is approximately $$W \approx \sum_{i=1}^n W_i \approx \sum_{i=1}^nF(x^∗_i) \Delta x. \nonumber$$ Taking the limit of this expression as $n \to \infty$ gives us the exact value for work: $$\begin{array}{rcl} W & = & \displaystyle \lim_{n \to \infty }\sum_{i=1}^nF(x^∗_i) \Delta x \\[16pt] & = & \displaystyle \int ^b_aF(x)dx. \\ \end{array} \nonumber$$ Thus, we can define work as follows.

Definition: Work

If a variable force $F(x)$ moves an object in a positive direction along the $x$-axis from point $a$ to point $b$, then the work done on the object is $$W=\int ^b_aF(x)\,dx. \label{IntWork}$$

Note that if $F$ is constant, the integral evaluates to $F \cdot (b−a)=F d$, which is Equation $\ref{BasicWork}$.

Example $\PageIndex{3}$

When a particle is located a distance $x$ meters from the origin, a force of $\cos⁡\left( \frac{\pi x}{3} \right)$ newtons acts on it. Compute the amount of work done on the particle in moving it between the following $x$-values.

1. From $x = 1$ to $x = 2$.
2. From $x=1$ to $x=1.5$.
3. From $x=1.5$ to $x=2$.

Solution

1. From Equation $\ref{IntWork}$, we get $$\begin{array}{rcl} W & = & \displaystyle \int_1^2 \cos\left( \dfrac{\pi x}{3} \right) \, dx \\[16pt] & = & \dfrac{3}{\pi} \sin\left( \dfrac{\pi x}{3} \right)\bigg|_{x=1}^{x = 2} \\[16pt] & = & \dfrac{3}{\pi} \left( \sin\left( \dfrac{2 \pi}{3} \right) - \sin\left( \dfrac{\pi}{3} \right) \right) \\[16pt] & = & \dfrac{3}{\pi} \left( \dfrac{\sqrt{3}}{2} - \dfrac{\sqrt{3}}{2} \right) \\[16pt] & = & 0 \\ \end{array} \nonumber$$ Therefore, no work is done on the particle in moving it from $x = 1$ to $x = 2$. If this seems strange, the next two parts might clarify what happened.
2. Repeating the setup from part a, we get $$\begin{array}{rcl} W & = & \displaystyle \int_1^{3/2} \cos\left( \dfrac{\pi x}{3} \right) \, dx \\[16pt] & = & \dfrac{3}{\pi} \sin\left( \dfrac{\pi x}{3} \right)\bigg|_{x=1}^{x = 3/2} \\[16pt] & = & \dfrac{3}{\pi} \left( \sin\left( \dfrac{\pi}{2} \right) - \sin\left( \dfrac{\pi}{3} \right) \right) \\[16pt] & = & \dfrac{3}{\pi} \left( 1 - \dfrac{\sqrt{3}}{2} \right) \\[16pt] & \approx & 0.1279 \\ \end{array} \nonumber$$ Thus, work of approximately $0.1279$ joules have been imparted to the particle over the interval $[1, 1.5]$.
3. For our final calculation, we get $$\begin{array}{rcl} W & = & \displaystyle \int_{3/2}^2 \cos\left( \dfrac{\pi x}{3} \right) \, dx \\[16pt] & = & \dfrac{3}{\pi} \sin\left( \dfrac{\pi x}{3} \right)\bigg|_{x=3/2}^{x = 2} \\[16pt] & = & \dfrac{3}{\pi} \left( \sin\left( \dfrac{2 \pi}{3} \right) - \sin\left( \dfrac{\pi}{2} \right) \right) \\[16pt] & = & \dfrac{3}{\pi} \left( \dfrac{\sqrt{3}}{2} - 1 \right) \\[16pt] & \approx & -0.1279 \\ \end{array} \nonumber$$ In this case, work of approximately $-0.1279$ joules have been extracted from the particle over the interval $[1.5, 2]$. The work done during the first 0.5 meters of movement is undone in the second 0.5 meter. This explains why the total amount of work done over the interval $[1,2]$ is zero.⁴

Spring-Mass Problems and Hooke's Law

Now let's look at the specific example of the work done to compress or elongate a spring. Consider a block attached to a horizontal spring.⁵ The block moves back and forth as the spring stretches and compresses. This type of problem is called a spring-mass system, and it is a common topic in Differential Equations. Although, in the real world, we would have to account for the friction between the block and the surface on which it is resting, we ignore this here and assume the block is resting on a frictionless surface. When the spring is at its natural length (at rest), the system is said to be at equilibrium. In this state, the spring is neither elongated nor compressed, and in this equilibrium position the block does not move until some force is introduced. We orient the system such that $x=0$ corresponds to the equilibrium position (Figure $\PageIndex{1}$).

Figure $\PageIndex{1}$: A block attached to a horizontal spring at equilibrium, compressed, and elongated.

According to Hooke's law, the force required to compress or stretch a spring from an equilibrium position is given by $$F(x) = kx, \label{HookesLaw}$$ where $k \gt 0$ depends on the physical characteristics of the spring and, as such, is called the spring constant. We can use this information to calculate the work done to compress or elongate a spring, as shown in the following example.

Example $\PageIndex{4}$: The Work Required to Stretch or Compress a Spring

Suppose it takes a force of $10$ N (in the negative direction) to compress a spring $0.2$ m from the equilibrium position. How much work is done to stretch the spring $0.5$ m from the equilibrium position?

Solution

First, we find the spring constant, $k$.

When $x=−0.2$, we know $F(x)=−10,$ so $$\begin{array}{rrcl} & F(x) & = & kx \\ \implies & −10 & = & k(−0.2) \\ \implies & k & = & 50 \\ \end{array} \nonumber$$ and $F(x)=50x$. Then, to calculate work, we integrate the force function, obtaining $$\begin{array}{rcl} W & = & \displaystyle \int ^b_aF(x) \, dx \\[16pt] & = & \displaystyle \int ^{0.5}_050 x \,dx \\[16pt] & = & 25x^2 \bigg|^{0.5}_0 \\[16pt] & = & 6.25. \\ \end{array} \nonumber$$ The work done to stretch the spring $0.5$ m from equilibrium is $6.25$ J.

Checkpoint $\PageIndex{4}$

Suppose it takes a force of $8$ lb to stretch a spring $6$ in. from the equilibrium position. How much work is done to stretch the spring $1$ ft from the equilibrium position?

Answer

$8$ ft-lb

Lifting Distributed Masses

Videos

• The Concept and Computation of the Work to Lift a Continuous Object
• Computing Work to Lift a Continuous Object Attached to a "Bucket"

In Example $\PageIndex{2}$, we lifted a simple object - a bucket filled with water. We can consider this bucket as a point mass. A point mass appropriately represents any object whenever its size, shape, and structure are irrelevant in a given context. That is, the shape and size of the bucket never entered our conversation when talking about lifting it - the mathematics doesn't change if we draw the bucket as a car, a dog, or a point. In fact, in the context of work, buckets, cars, dogs, books, baseballs, and dumbbells are all examples of point masses. There is no difference in the work done lifting them if we compress them to a single point with the same mass.

A distributed mass, on the other hand, refers to a system where the mass is spread out or distributed over a certain region or volume, instead of being concentrated at a single point. It is often used to describe objects or systems that have a continuous mass distribution. For our purposes, we will consider an object to be a distributed mass if we cannot consider it a point mass. Therefore, chains, cables, and ropes are all common examples of distributed masses in this text.

Computing the work to lift an object that can be considered a point mass is simple - replace the object with a point having the same mass and compute the work necessary to lift it using Equations $\ref{BasicWork}$, $\ref{ForceWork}$, or $\ref{IntWork}$.

Computing the work to lift an object that cannot be considered a point mass (and is, therefore, a distributed mass) requires a little more thinking. For example, if we had a cable of length $\mathcal{l}$ hanging over a cliff of height $h$ that we needed to pull to the top, we would consider that cable to be a distributed mass. As we pull the cable, the weight we are lifting (the force) becomes less and less because there is less cable to lift. How do we account for this phenomenon mathematically?

As with most of our processes in mathematics, we start by drawing a picture to help us conceptualize what is going on.

Figure $\PageIndex{2}$: A cable hanging from the edge of a cliff.

I like to place the bottom of the cable on the $x$-axis, but if you prefer (or your instructor prefers) to place the $x$-axis at the top of the cliff, the only difference will be minor perspective changes.

Lifting the entire cable to the top of the cliff is the same as lifting small segments (slices) of the cable to the top, one by one. That is, we will partition the $y$-interval, $\left[ h - \mathcal{l} ,h \right]$ into $n$ equally-spaced subintervals. We need to compute the work required to lift the $i^{\text{th}}$ slice to the top of the cliff. From Equation $\ref{BasicWork}$, we know that $$W_i = F_i d_i, \nonumber$$ where $F_i$ is the weight of the $i^{\text{th}}$ slice and $d_i$ is the distance the $i^{\text{th}}$ slice needs to move to get to the top of the cliff. If we let $y_i^* \in \left[ y_{i-1}, y_i \right]$, then the distance from the $i^{\text{th}}$ slice to the top of the cliff is approximately $d_i^* = h - y_i^*$ (see Figure $\PageIndex{3}$ below).

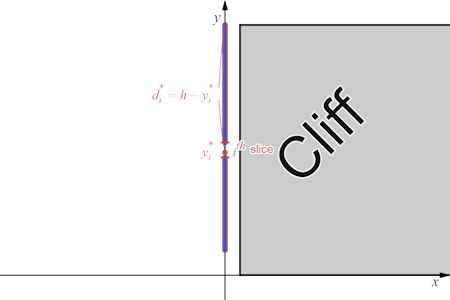
Figure $\PageIndex{3}$: Lifting the $i^{\text{th}}$ slice a distance $d_i^*$.

That is, $$W_i \approx F_i d_i^* = F_i \left( h - y_i^* \right). \nonumber$$ Moreover, if $F$ represents the force (weight) of the entire cable we need to lift, we can compute the unit force of the cable, $\frac{F}{\mathcal{l}}$, and multiply that result by the width of the $i^{\text{th}}$ slice, $\Delta y$, to arrive at $$F_i = \dfrac{F}{\mathcal{l}} \cdot \Delta y. \nonumber$$ A little unit analysis shows that our argument is solid: since the unit length is in pounds per foot and $\Delta y$ is in feet, the result is in pounds - a force!

In the end, the work to lift the $i^{\text{th}}$ slice is $$W_i \approx F_i d_i^* = F_i \left( h - y_i^* \right) = \dfrac{F}{\mathcal{l}} \Delta y \left( h - y_i^* \right). \nonumber$$ As we have done many times up to this point, we would sum all of these little pieces of work, which creates a Riemann sum, take the limit as $n \to \infty$, and arrive at an integral; however, rather than providing a closed-form integral, it's best to derive a proper integral for each situation - this is because these types of problems can vary wildly, and knowing the derivation will provide you with a much better understanding of the physics in the background.

Example $\PageIndex{5}$: The Work Required to Lift a Bucket (Part 2)

A chain is attached to a 5-liter bucket which is filled with molten gold. The bucket has a mass of 80 kg (it has to be made of strong stuff to hold molten metals). The chain has a mass of 3.1 kg per meter. How much work is done in lifting the bucket from the bottom of a 60-meter-deep well? (Molten gold has a density of $\rho_{\text{g}} = 17,310 \, \text{kg}/\text{m}^3$, and $1,000 \, \text{L} = 1 \, \text{m}^3$).

Solution

It is wise to treat this problem as lifting two separate masses - the point mass (the bucket of molten gold) and the distributed mass (the chain).

Work to Lift the Point Mass

The work to lift the bucket is $$\begin{array}{rcl} W_{\text{b}} & = & F_{\text{b}} d_{\text{b}} \\[16pt] & = & \left(m_{\text{b}} + m_{\text{g}}\right) g d_{\text{b}} \\[16pt] & \approx & \left( 80 \, \text{kg} + \rho_{\text{g}} V_{\text{g}} \right) \left( 9.8 \, \text{m}/\text{s}^2 \right) \left( 60 \, \text{m} \right) \\[16pt] & \approx & \left( 80 \, \text{kg} + 17,310 \, \frac{\text{kg}}{\text{m}^3} \cdot 5 \, \text{L} \right) \left( 9.8 \, \frac{\text{m}}{\text{s}^2} \right) \left( 60 \, \text{m} \right) \\[16pt] & = & \left( 80 \, \text{kg} + 17,310 \, \frac{\text{kg}}{\cancel{\text{m}^3}} \cdot 5 \, \frac{1}{1000} \, \cancel{\text{m}^3} \right) \left( 9.8 \, \frac{\text{m}}{\text{s}^2} \right) \left( 60 \, \text{m} \right) \\[16pt] & = & \left( 80 \, \text{kg} + 86.55 \, \text{kg} \right) \left( 9.8 \, \frac{\text{m}}{\text{s}^2} \right) \left( 60 \, \text{m} \right) \\[16pt] & = & \left( 166.55 \right) \left( 9.8 \right) \left( 60 \right) \frac{\text{kg m}}{\text{s}^2} \cdot \text{m} \\[16pt] & \approx & 97,931 \, \text{J} \\ \end{array} \nonumber$$

Work to Lift the Distributed Mass

The work to lift the $i^{\text{th}}$ slice of the chain is $$W_i = F_i d_i = m_i g d_i \approx \left(9.8 \frac{\text{m}}{\text{s}^2} \right) m_i d_i. \nonumber$$ Assuming the bottom of the well is the $x$-axis and $y_i^* \in \left[ y_{i-1}, y_i \right]$, then $d_i \approx d_i^* = 60 \, \text{m} - y_i^* \, \text{m} = \left( 60 - y_i^* \right) \, \text{m}$. Therefore, $$W_i \approx \left(9.8 \frac{\text{m}}{\text{s}^2} \right) m_i \left( 60 - y_i^* \right) \, \text{m}. \nonumber$$ To compute the mass of the $i^{\text{th}}$ slice, we need the mass per unit length of the chain and then we need to multiply that by the width of the $i^{\text{th}}$ slice. Luckily, we were told the mass per unit length of the chain was $3.1$ kg per meter. Thus, $m_i = \left( 3.1 \, \frac{\text{kg}}{\cancel{\text{m}}} \right) \Delta y \, \cancel{\text{m}} = 3.1 \Delta y \, \text{kg}$. Therefore, $$W_i \approx \left(9.8 \frac{\text{m}}{\text{s}^2} \right) \left(3.1 \Delta y \, \text{kg} \right) \left( 60 - y_i^* \right) \, \text{m} = (9.8)(3.1) (60 - y_i^*) \Delta y \, \text{J}. \nonumber$$ Forming a Riemann sum, taking the limit, and transposing it into an integral, we get the work to lift the chain (by itself) to be $$\begin{array}{rcl} W_{\text{c}} & = & \displaystyle \int_{y = 0}^{y = 60} (9.8)(3.1)(60 - y) \, dy \\[16pt] & = & 30.38 \left( 60y - \frac{y^2}{2} \right) \bigg|_0^{60} \\[16pt] & = & 54,684 \, \text{J} \\ \end{array} \nonumber$$

Total Work

We now need to add these two computations. $$W = W_{\text{b}} + W_{\text{c}} \approx 152,615 \, \text{J}. \nonumber$$

The limits of the integral in Example $\PageIndex{5}$ can be read as, "We are moving slices starting at the height of $y = 0$ and ending at the height of $y = 60$." It is important to understand this. If the well were 60 meters deep, but we were only lifting the chain 10 meters, then we would consider the length of the chain from $y = 0$ to $y = 50$ as a point mass being lifted only 10 meters. We would then lift the upper 10 meters using the integral $$\int_{y = 50}^{y = 60} (9.8)(3.1)(60 - y) \, dy, \nonumber$$ because it is only that section that loses mass as we lift the chain.

Lifting Point Masses that Gain or Lose Mass

Videos

• Computing Work to Lift a Continuous Object with a "Leaky Bucket"
• Compute Work to Partially Lift a Rope Attached to a "Leaky Bucket"

Suppose an object is a point mass that starts with a mass of $m_{\text{initial}}$ and ends with a mass $m_{\text{final}}$, where $m_{\text{initial}} \neq m_{\text{final}}$ and where the gain or loss of mass is linear (i.e., the mass gains or loses the same amount of mass per unit length). For purposes of this discussion, we will assume that the object has lost mass. Still, you only need to adjust a single part of your thought process to accommodate an object gaining mass.

To see how we approach this type of problem, it's best to consider an example.

Example $\PageIndex{6}$: The Work Required to Lift a Bucket (Part 3)

A chain is attached to a 5-liter leaky bucket which is filled with molten gold. The leak is such that the molten gold drains from the bucket at a constant rate, and by the time the bucket reaches the top of the well, the bucket is 80% empty. The bucket has a mass of 80 kg. The chain has a mass of 3.1 kg per meter. How much work is done in lifting the bucket from the bottom of a 60-meter-deep well? (Molten gold has a density of $\rho_{\text{g}} = 17,310 \, \text{kg}/\text{m}^3$, and $1,000 \, \text{L} = 1 \, \text{m}^3$).

Solution

Again, we treat this as two separate problems - the leaky point mass (the leaky bucket of molten gold) and the distributed mass (the chain).

Work to Lift the Leaky Point Mass

From our previous work, we know that the bucket and the molten gold have a combined mass of $166.55$ kg; however, we are now told that the bucket loses 80% of mass due to molten gold by the time it reaches the top of the well. Since it drained at a constant rate, we can safely say that the bucket loses $0.80 \left( \frac{1731}{20} \right) = 69.24$ kg of mass over the 60-meter lift. That is, it loses $1.154$ kg per meter.

Consider partitioning the interval $[0,60]$ into $n$ equally-spaced subintervals. The distance to move the mass from $y_{i-1}$ to $y_i$ is $\Delta y$. Therefore, the work needed to lift this mass in this small interval is $$W_i = F_i d_i = m_i g d_i = m_i \left( 9.8 \, \frac{\text{m}}{\text{s}^2} \right) \Delta y. \nonumber$$ If $y_i^* \in [y_{i-1}, y_i]$, then we can consider the mass of the object in the small interval $[y_{i-1},y_i]$ to approximately be $$m_i^* \approx m_{\text{initial}} - m_{\text{lost}} = 166.55 \, \text{kg} - 1.154 \, \frac{\text{kg}}{\cancel{\text{m}}} y_i^* \cancel{\text{m}} = (166.55 - 1.154 y_i^*) \, \text{kg}.\nonumber$$ Thus, the work to lift the leaky bucket is $$\begin{array}{rcl} W_{\text{b}} & = & \displaystyle \int_{y = 0}^{y = 60} (166.55 - 1.154 y) (9.8) dy \\[16pt] & = & 9.8 \left( 166.55y - 0.577 y^2 \right)\bigg|_{y = 0}^{y = 60} \\[16pt] & = & 77,574.84 \, \text{J} \\ \end{array} \nonumber$$

Work to Lift the Distributed Mass

Nothing changes about this part, so we can use the 54,684 J computed previously.

Total Work

The total work done is $$W = W_{\text{b}} + W_{\text{c}} = 132,258.84 \, \text{J}. \nonumber$$ A quick logic check helps here. Notice this is less work than before. That should make sense as we are lifting a bucket with a hole!

Lifting Fluids

Consider the work done to pump water (or some other liquid) out of a tank. Pumping problems are more complicated than spring problems because many of the calculations depend on the shape and size of the tank. In addition, instead of being concerned about the work done to move a single mass, we are looking at the work done to move a volume of water. It takes more work to move the water from the bottom of the tank (which has to be moved farther) than moving the water from the top of the tank.

We examine the process in the context of a cylindrical tank, then look at a couple of examples using tanks of different shapes.

Assume a cylindrical tank of radius $4$ m and height $10$ m is filled to a depth of $8$ m. How much work does it take to pump all the water over the top edge of the tank?

The first thing we need to do is define a frame of reference. We let $x$ represent the vertical distance below the top of the tank. That is, we orient the $x$-axis vertically, with the origin at the top of the tank and the downward direction being positive (Figure $\PageIndex{4}$).⁶

Figure $\PageIndex{4}$: How much work is needed to empty a tank partially filled with water?

Using this coordinate system, the water extends from $x=2$ to $x=10$.⁷ Therefore, we partition the interval $[2,10]$ and look at the work required to lift each individual "layer" of water. So, for $i=0,1,2, \ldots ,n$, let $P={x_i}$ be a regular partition of the interval $[2,10]$, and for $i=1,2, \ldots ,n$, choose an arbitrary point $x^∗_i \in [x_{i−1},x_i]$. Figure $\PageIndex{5}$ shows a representative layer.⁸

Figure $\PageIndex{5}$: A representative layer of water.

In pumping problems, the force required to lift the water to the top of the tank is the force required to overcome gravity, so it is equal to the weight of the water. In the metric system, the density of water is $\rho_{\text{w}} = 1000 \, \text{kg/m}^3$, which means the weight density is $$\gamma_{\text{w}} = \rho_{\text{w}} g \approx 1000 \, \frac{\text{kg}}{\text{m}^3} \cdot 9.8 \, \frac{\text{m}}{\text{s}^2} = 9800 \, \frac{\text{kg m}/\text{s}^2}{\text{m}^3} = 9800 \, \frac{\text{N}}{\text{m}^3}.$$ In the U.S. Customary System, the weight density of water is $\gamma_{\text{w}} \approx 62.4\,\text{lb/ft}^3$.

Calculating the volume of each layer gives us the weight. In this case, we have $$V = \pi (4)^2 \Delta x=16 \pi \Delta x. \nonumber$$ The force needed to lift each layer is $$F = 9800 \cdot 16 \pi \Delta x=156,800 \pi \Delta x. \nonumber$$ Note that this step becomes a little more difficult if we have a noncylindrical tank (that will be our next example).

We also need to know the distance the water must be lifted. Based on our choice of coordinate systems, we can use $x^∗_i$ as an approximation of the distance the layer must be lifted.⁹ Then the work to lift the $i^{\text{th}}$ layer of water $W_i$ is approximately¹⁰ $$W_i \approx 156,800 \pi x^∗_i \Delta x. \nonumber$$ Adding the work for each layer, we see the approximate work to empty the tank is given by $$\begin{array}{rcl} W & \approx & \displaystyle \sum_{i=1}^nW_i \\[16pt] & \approx & \displaystyle \sum_{i=1}^n156,800 \pi x^∗_i \Delta x. \\ \end{array} \nonumber$$ This is a Riemann sum, so taking the limit as $n \to \infty ,$ we get $$\begin{array}{rcl} W & = & \displaystyle \lim_{n \to \infty }\sum^n_{i=1}156,800 \pi x^∗_i \Delta x \\[16pt] & = & 156,800 \pi \displaystyle \int ^{10}_2x \, dx \\[16pt] & = & 156,800 \pi \left( \dfrac{x^2}{2}\right)\bigg|^{10}_2 \\[16pt] & = & 7,526,400 \pi \\[16pt] & \approx & 23,644,883. \\ \end{array} \nonumber$$ The work required to empty the tank is approximately 23,650,000 J.¹¹

For pumping problems, the calculations vary depending on the shape of the tank or container. The following problem-solving strategy lays out a step-by-step process for solving pumping problems.

Problem-Solving Strategy: Solving Pumping Problems

1. Sketch a picture of the tank and select an appropriate frame of reference.
2. Calculate the volume of a representative layer of water.
3. Multiply the volume by the weight-density of water to get the force.
4. Calculate the distance the layer of water must be lifted.
5. Multiply the force and distance to estimate the work needed to lift the layer of water.
6. Sum the work required to lift all the layers. This expression is an estimate of the work needed to pump out the desired amount of water, and it is in the form of a Riemann sum.
7. Take the limit as $n \to \infty$ and evaluate the resulting integral to get the exact work required to pump out the desired amount of water.

We now apply this problem-solving strategy in an example with a noncylindrical tank.

Example $\PageIndex{7}$: A Pumping Problem with a Noncylindrical Tank

Assume a tank in the shape of an inverted cone, with height $12$ ft and base radius $4$ ft. The tank is full to start with, and water is pumped over the upper edge of the tank until the height of the water remaining in the tank is $4$ ft. How much work is required to pump out that amount of water?

Solution

The tank is depicted in Figure $\PageIndex{6}$. As we did in the example with the cylindrical tank, we orient the $x$-axis vertically, with the origin at the top of the tank and the downward direction being positive.

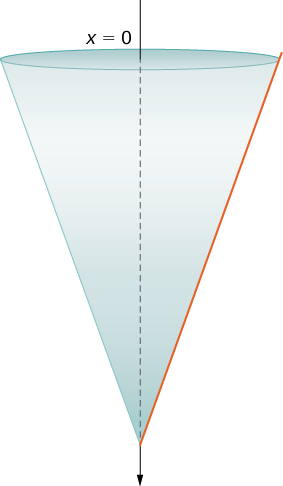
Figure $\PageIndex{6}$: A water tank shaped like an inverted cone.

The tank starts out full and ends with $4$ ft of water left, so, based on our chosen frame of reference, we need to partition the interval $[0,8]$. Then, for $i=0,1,2, \ldots ,n$, let $P={x_i}$ be a regular partition of the interval $[0,8]$, and for $i=1,2, \ldots ,n$, choose an arbitrary point $x^∗_i \in [x_{i−1},x_i]$. We can approximate the volume of a layer by using a disk, then use similar triangles to find the radius of the disk (Figure $\PageIndex{7}$).

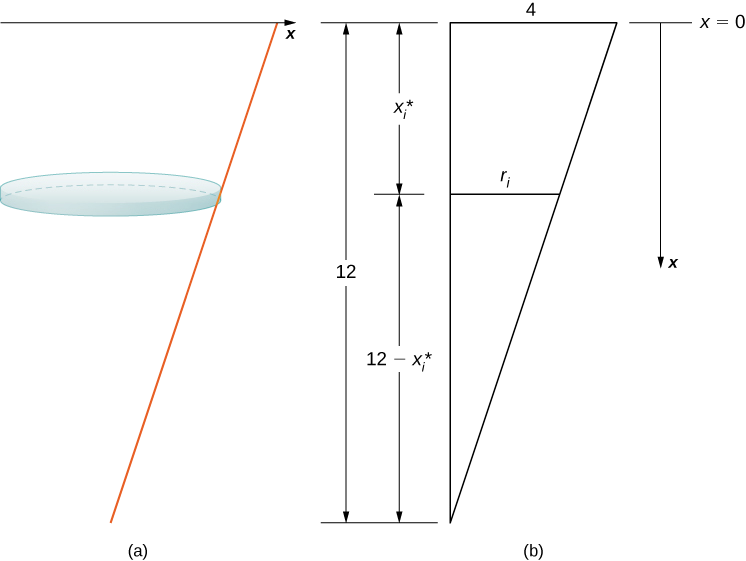
Figure $\PageIndex{7}$: Using similar triangles to express the radius of a disk of water.

From properties of similar triangles, we have $$\begin{array}{rrcl} & \dfrac{r_i}{12−x^∗_i} & = & \dfrac{4}{12} =\dfrac{1}{3} \\[16pt] \implies & 3r_i & = & 12−x^∗_i \\[16pt] \implies & r_i & = & \dfrac{12−x^∗_i}{3} \\[16pt] \implies & r_i & = & 4−\dfrac{x^∗_i}{3}. \\ \end{array} \nonumber$$ Then the volume of the disk is $$V_i = \pi \left(4−\dfrac{x^∗_i}{3}\right)^2\, \Delta x. \nonumber$$ The weight density of water is $62.4 \text{ lb/ft}^3$, so the force needed to lift each layer is approximately $$F_i \approx 62.4 \pi \left(4−\dfrac{x^∗_i}{3}\right)^2\, \Delta x \nonumber$$ Based on the diagram, the distance the water must be lifted is approximately $x^∗_i$ feet, so the approximate work needed to lift the layer is $$W_i \approx 62.4 \pi x^∗_i\left(4−\dfrac{x^∗_i}{3}\right)^2\, \Delta x. \nonumber$$ Summing the work required to lift all the layers, we get an approximate value of the total work: $$W=\sum_{i=1}^nW_i \approx \sum_{i=1}^n62.4 \pi x^∗_i \left(4−\dfrac{x^∗_i}{3}\right)^2\, \Delta x. \nonumber$$ Taking the limit as $n \to \infty ,$ we obtain $$\begin{array}{rcl} W & = & \displaystyle \lim_{n \to \infty }\sum^n_{i=1}62.4 \pi x^∗_i(4−\dfrac{x^∗_i}{3})^2 \Delta x \\[16pt] & = & \displaystyle \int ^8_062.4 \pi x \left(4−\dfrac{x}{3}\right)^2 \, dx \\[16pt] & = & 62.4 \pi \displaystyle \int ^8_0x \left(16−\dfrac{8x}{3}+\dfrac{x^2}{9}\right)\,dx \\[16pt] & = & 62.4 \pi \displaystyle \int ^8_0 \left(16x−\dfrac{8x^2}{3}+\dfrac{x^3}{9}\right)\,dx \\[16pt] & = & 62.4 \pi \left[8x^2−\dfrac{8x^3}{9}+\dfrac{x^4}{36}\right]\bigg|^8_0 \\[16pt] & = & 10,649.6 \pi \\[16pt] & \approx & 33,456.7. \\ \end{array}\nonumber$$ It takes approximately $33,450$ ft-lb of work to empty the tank to the desired level.¹²

Checkpoint $\PageIndex{7}$

A tank is shaped like an inverted cone, with height $10$ ft and a base radius of 6 ft. The tank is filled to a depth of 8 ft to start with, and water is pumped over the upper edge of the tank until 3 ft of water remains in the tank. How much work is required to pump out that amount of water?

Answer

Approximately $43,255.2$ ft-lb

---

Footnotes

¹ In more complex systems, you could have several factors contributing different accelerations. For example, in a car, you experience acceleration due to gravity (otherwise, your car would begin to rise in the air) and acceleration due to the movement of the car.

² For a great diversion into why some argue the unit of force in the metric system is the Newton, and not the newton, I encourage the reader to take a look at this excerpt by the Australian physicist, Don Koks.

³ We do not say, "The bucket has a weight of 2 kg," because kilograms is a measure of mass - weight is a measure of force. Mass is unchangeable (unless something gets added to or removed from the object); however, weight can change depending on the mass of the planet and your position on that planet. That is, according to Equation $\ref{Force}$, the 2-kg bucket has a weight of $$F = mg \approx \left( 2 \, \text{kg} \right)\left( 9.8 \, \frac{\text{kg m}}{\text{s}^2} \right) \approx 19.6 \, \text{N}\nonumber$$ at sea level on the Earth. However, on the surface of Jupiter, the bucket will still have a mass of 2 kg, but its weight would be $$F = mg \approx \left( 2 \, \text{kg} \right)\left( 24.5 \, \frac{\text{kg m}}{\text{s}^2} \right) = 49 \, \text{N}. \nonumber$$

⁴ As confounding as this might seem, from a physics perspective it is correct. The "tripping" point for most students is a perspective issue. For example, if a book is lifted straight up 3 feet and then lowered the same 3 feet, it makes sense to all of us that we expended energy in the lifting and lowering process; however, we need to change our perspective when it comes to work problems and physics. Instead of asking how much work (energy) have we have spent, we need to focus on how much work (energy) the object (the book) has gained or lost over that process. This concept is related to the conservation of energy. When you lift the object, you provide potential energy to it, which is converted from the energy you expend. When you lower the object back down, the potential energy is converted back into the same amount of energy you initially provided. No additional work is done on the object in the overall process.

⁵ The choice of having the spring oriented horizontally is not essential. We could have written this entire derivation assuming the spring was attached to the ceiling and oriented vertically. In that case, the block would have been connected to the bottom of the spring. It is important to clarify that, in the vertical orientation, the equilibrium position is the point where the restorative force of the spring is counteracted by the weight of the mass. That is, the equilibrium position would be where the spring stretches to once the mass is attached.

⁶ Your instructor might take a different approach for the frame of reference for fluid-work problems. For example, it is perfectly acceptable to place the bottom of the tank on the $x$-axis (centered at the origin) and still consider the upward direction as the positive $y$-axis - this is how I normally teach it.

⁷ Or, from $y = 0$ to $y = 8$, if your instructor is using the standard coordinate system.

⁸ Again, if your instructor is using the standard coordinate system, then the intervals are $[0,8]$.

⁹ If using the standard coordinate system, the layer we are considering is at a "height" (from the bottom of the tank) of $y_i^*$ m. To move this layer to the top of the tank, we must move it $\left( 10 - y_i^* \right)$ m.

¹⁰ Again, if using the standard coordinate system, the work to lift this $i^{\text{th}}$ layer is $W_i = F_i \times d_i \approx 156,800 \pi \times \left( 10 - y_i^* \right)$.

¹¹ You would have reached this same value using the standard coordinate system and computing $$W = \displaystyle \int_{y=0}^{y=8} 156,800 \pi (10 - y) \, dy. \nonumber$$ Conceptually, you would read this as, "I am lifting plates of fluid, starting at a height of 0 meters (the bottom), and the final plate is at a height of 8 meters. Each plate weighs $156,800$ newtons and is being lifted $10$ minus its height in meters."

¹² Done using the standard coordinate system, we would place the bottom of the tank on the $x$-axis, centered at the origin. We would need to lift the slices of water starting with the slice at $y = 4$ feet and ending with the slice at $y = 12$ feet (leaving the bottom 4 feet). The volume of the $i^{\text{th}}$ slice is $$V_i = \text{surface area} \times \Delta y = \pi r_i^2 \Delta y. \nonumber$$ Visually, we can see that $r_i = x_i^*$, but we need a relationship between $x_i^*$ and $y_i^*$ to continue. Luckily, we can find the equation of the edge of the tank. It's a line going through the origin having slope $\frac{12}{4} = 3$. Hence, $y_i^* = 3 x_i^*$. That is, $x_i^* = \frac{y_i^*}{3}$. Therefore, $$V_i = \pi \left( \dfrac{y_i^*}{3} \right)^2 \Delta y = \dfrac{\pi}{9} \left(y_i^*\right)^2 \Delta y. \nonumber$$ Hence, the force needed to lift this layer is $$F_i \approx 62.4 \cdot \dfrac{\pi}{9} \left(y_i^*\right)^2 \Delta y. \nonumber$$ We need to lift this layer $\left( 12 - y_i^* \right)$ feet, so the work done moving this specific layer is $$W_i \approx 62.4 \cdot \dfrac{\pi}{9} \left(y_i^*\right)^2 \left(12 - y_i^*\right) \Delta y. \nonumber$$ Thus, $$W = 62.4 \cdot \dfrac{\pi}{9} \int_{y = 4}^{y = 12} y^2 (12-y) \, dy \nonumber$$ This will become approximately 33,456.7 ft-lb.

---

Key Concepts

• Several physical applications of the definite integral are common in engineering and physics.
• Work can also be calculated by integrating a force function or counteracting the force of gravity, as in a pumping problem.

---

Key Equations

• Work done on an object

$W=\int ^b_aF(x)dx$

---

Glossary

Hooke’s law

this law states that the force required to compress (or elongate) a spring is proportional to the distance the spring has been compressed (or stretched) from equilibrium; in other words, $F=kx$, where $k$ is a constant

work

the amount of energy it takes to move an object; in physics, when a force is constant, work is expressed as the product of force and distance