5.4E: Exercises for Section 5.4

Exercise 1

1. Given \(\mathbf r(t)=(3t^2−2)\,\mathbf{i}+(2t−\sin t)\,\mathbf{j}\):

1. Find the velocity of a particle moving along this curve.
2. Find the acceleration of a particle moving along this curve.

Figure \(\PageIndex{1}\): This is the graph of the given vector function representing the position. lt's a curve in the \(xy\)-plane that widens symmetrically about the \(x\)-axis, as it moves to the right along the \(x\)-axis. The curve begins at the origin \((-2,0)\) and expands to the right, forming a shape like a narrow flap of an envelope.

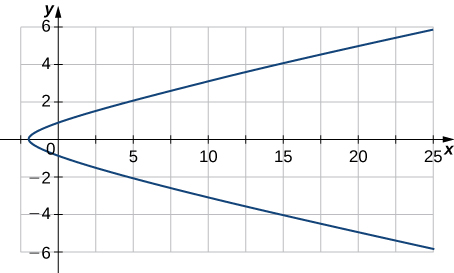
Answer

1. \(\mathbf v(t)=6t\,\mathbf{i}+(2−\cos t)\,\mathbf{i}\)
2. \(\mathbf a(t)=6\,\mathbf{i}+\sin t\,\mathbf{i}\)

Exercises 2 - 5

Given the position function, find the velocity, acceleration, and speed in terms of the parameter \(t\).

2. \(\mathbf r(t)=e^{−t}\,\mathbf{i}+t^2\,\mathbf{j}+\tan t\,\mathbf{k}\)
3. \(\mathbf r(t)=⟨3\cos t,\,3\sin t,\,t^2⟩\)

Answer

\(\mathbf v(t)=-3\sin t\,\mathbf{i}+3\cos t\,\mathbf{j}+2t\,\mathbf{k}\)
\(\mathbf a(t)=-3\cos t\,\mathbf{i}-3\sin t\,\mathbf{j}+2\,\mathbf{k}\)
\(\text{Speed}(t) = \|\mathbf v(t)\| = \sqrt{9 + 4t^2}\)

4. \(\mathbf r(t)=t^5\,\mathbf{i}+(3t^2+2t- 5)\,\mathbf{j}+(3t-1)\,\mathbf{k}\)
5. \(\mathbf r(t)=2\cos t\,\mathbf{j}+3\sin t\,\mathbf{k}\). The graph is shown here:

Figure \(\PageIndex{2}\): The graph of the given vector function is an ellipse graphed in the three-dimensional space. The ellipse is contained in tye \(yz\)-plane, with its major axis along the \(z\)-axis and minor axis along the \(y\)-axis.

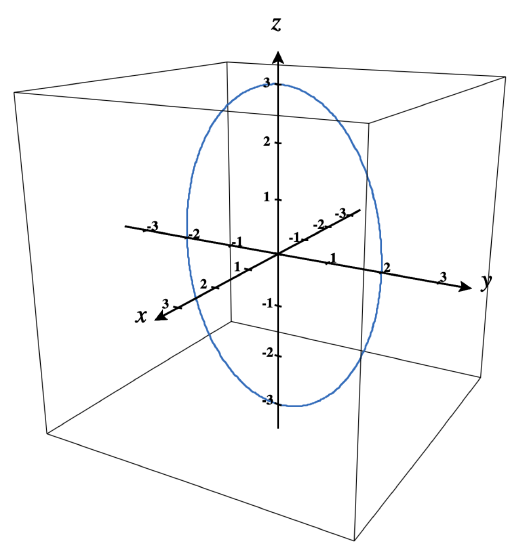
Answer

\(\mathbf v(t)=-2\sin t\,\mathbf{j}+3\cos t\,\mathbf{k}\)
\(\mathbf a(t)=-2\cos t\,\mathbf{j}-3\sin t\,\mathbf{k}\)
\(\text{Speed}(t) = \|\mathbf v(t)\| = \sqrt{4\sin^2 t+9\cos^2 t}=\sqrt{4+5\cos^2 t}\)

Exercises 6 - 8

Find the velocity, acceleration, and speed of a particle with the given position function.

6. \(\mathbf r(t)=⟨t^2−1,t⟩\)
7. \(\mathbf r(t)=⟨e^t,e^{−t}⟩\)

Answer

\(\mathbf v(t)=⟨e^t,−e^{−t}⟩\),
\(\mathbf a(t)=⟨e^t, e^{−t}⟩,\)
\( \|\mathbf v(t)\| = \sqrt{e^{2t}+e^{−2t}}\)

8. \(\mathbf r(t)=⟨\sin t,t,\cos t⟩\). The graph is shown here:

Figure \(\PageIndex{3}\): The graph of the given vector function is a curve that forms a smooth arc. The plot is enclosed within a rectangular box with the horizontal axis ranging from -1 to 1, the vertical axis ranging from -0.5 to 1, and the depth axis ranging from -2 to 2. The curve goes from lower-left front, rises to a peak near the center, and then descends as it moves toward the lower-right back.

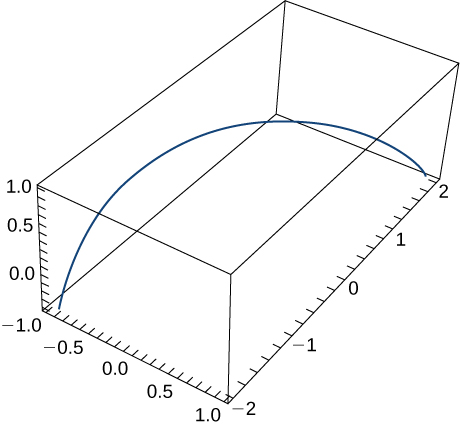
9. The position function of an object is given by \(\mathbf r(t)=⟨t^2,5t,t^2−16t⟩\). At what time is the speed a minimum?

Answer

\(t = 4\)

10. Let \(\mathbf r(t)=r\cosh(ωt)\,\mathbf{i}+r\sinh(ωt)\,\mathbf{j}\). Find the velocity and acceleration vectors and show that the acceleration is proportional to \(\mathbf r(t)\).
11. Consider the motion of a point on the circumference of a rolling circle. As the circle rolls, it generates the cycloid \(\mathbf r(t)=(ωt−\sin(ωt))\,\mathbf{i}+(1−\cos(ωt))\,\mathbf{j}\), where \(\omega\) is the angular velocity of the circle and \(b\) is the radius of the circle:

Figure \(\PageIndex{4}\): This is the graph of the given cycloid in the Cartesian plane. The curve alternates between peaks and valleys, with peaks occurring at \(y=4\) and valleys touching the \(x\)-axis at regular intervals, \(x = 4n\pi\), with \(n\) an integer.

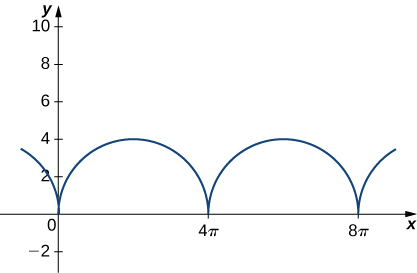
Find the equations for the velocity, acceleration, and speed of the particle at any time.

Answer

\(\mathbf v(t)=(ω−ω\cos(ωt))\,\mathbf{i}+(ω\sin(ωt))\,\mathbf{j}\)
\(\mathbf a(t)=(ω^2\sin(ωt))\,\mathbf{i}+(ω^2\cos(ωt))\,\mathbf{j}\)
\(\begin{align*} \text{speed}(t) &= \sqrt{(ω−ω\cos(ωt))^2 + (ω\sin(ωt))^2} \\
&= \sqrt{ω^2 - 2ω^2 \cos(ωt) + ω^2\cos^2(ωt) + ω^2\sin^2(ωt)} \\
&= \sqrt{2ω^2(1 - \cos(ωt))} \end{align*} \)

12. A person on a hang glider is spiraling upward as a result of the rapidly rising air on a path having position vector \(\mathbf r(t)=(3\cos t)\,\mathbf{i}+(3\sin t)\,\mathbf{j}+t^2\,\mathbf{k}\). The path is similar to that of a helix, although it is not a helix. The graph is shown here:

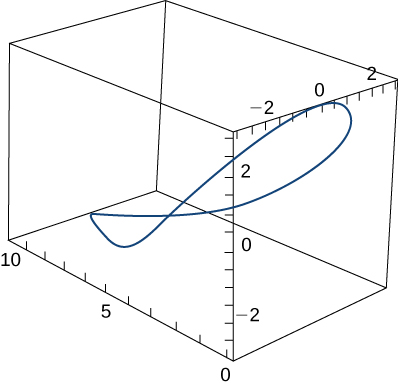
Figure \(\PageIndex{5}\): The graph of the given vector function is a curve that forms a smooth arc. The plot is enclosed within a rectangular box with the horizontal axis ranging from 10 to 0, the vertical axis ranging from -3 to 3, and the depth axis ranging from -3 to 3. The curve is a closed loop. The curve begins near the bottom-left corner of the graph, rises as it moves to the right, turns around, and then descends back to the starting point, forming a shape the like boundary of a "potato chip".

Find the following quantities:

1. The velocity and acceleration vectors
2. The glider’s speed at any time
3. The times, if any, at which the glider’s acceleration is orthogonal to its velocity

Answer

2. \(\|\mathbf v(t)\|=\sqrt{9+4t^2}\)

13. Given that \(\mathbf r(t)=⟨e^{−5t}\sin t,\, e^{−5t}\cos t,\, 4e^{−5t}⟩\) is the position vector of a moving particle, find the following quantities:

1. The velocity of the particle
2. The speed of the particle
3. The acceleration of the particle

Answer

1. \(\mathbf v(t)=⟨e^{−5t}(\cos t−5\sin t),\, −e^{−5t}(\sin t+5\cos t),\, −20e^{−5t}⟩\)

3. \(\mathbf a(t)=⟨e^{−5t}(−\sin t−5\cos t)−5e^{−5t}(\cos t−5\sin t), \; −e^{−5t}(\cos t−5\sin t)+5e^{−5t}(\sin t+5\cos t),\; 100e^{−5t}⟩\)

14. Find the maximum speed of a point on the circumference of an automobile tire of radius \(1\) ft when the automobile is traveling at \(55\) mph.
15. Find the position vector-valued function \(\mathbf r(t)\), given that \(\mathbf a(t)=\mathbf{i}+e^t \,\mathbf{j}, \quad \mathbf v(0)=2\,\mathbf{j}\), and \(\mathbf r(0)=2\,\mathbf{i}\).
16. Find \(\mathbf r(t)\) given that \(\mathbf a(t)=−32\,\mathbf{j}, \mathbf v(0)=600\sqrt{3} \,\mathbf{i}+600\,\mathbf{j}\), and \(\mathbf r(0)=\mathbf 0\).
17. The acceleration of an object is given by \(\mathbf a(t)=t\,\mathbf{j}+t\,\mathbf{k}\). The velocity at \(t=1\) sec is \(\mathbf v(1)=5\,\mathbf{j}\) and the position of the object at \(t=1\) sec is \(\mathbf r(1)=0\,\mathbf{i}+0\,\mathbf{j}+0\,\mathbf{k}\). Find the object’s position at any time.

Answer

\(\mathbf r(t)=0\,\mathbf{i}+\left(\frac{1}{6}t^3+4.5t−\frac{14}{3}\right)\,\mathbf{j}+\left(\frac{1}{6}t^3−\frac{1}{2}t+\frac{1}{3}\right)\,\mathbf{k}\)

Exercises 18 - 22

Projectile Motion

18. A projectile is shot in the air from ground level with an initial velocity of \(500\) m/sec at an angle of 60° with the horizontal.

1. At what time does the projectile reach maximum height?
2. What is the approximate maximum height of the projectile?
3. At what time is the maximum range of the projectile attained?
4. What is the maximum range?
5. What is the total flight time of the projectile?

Answer

1. \(44.185\) sec

3. \(t=88.37\) sec

5. \(t=88.37\) sec

19. A projectile is fired at a height of \(1.5\) m above the ground with an initial velocity of \(100\) m/sec and at an angle of 30° above the horizontal. Use this information to answer the following questions:
    1. Determine the maximum height of the projectile.
    2. Determine the range of the projectile.

Answer

The range is approximately \(886.29\) m.

20. A golf ball is hit in a horizontal direction off the top edge of a building that is 100 ft tall. How fast must the ball be launched to land \(450\) ft away?
21. A projectile is fired from ground level at an angle of 8° with the horizontal. The projectile is to have a range of \(50\) m. Find the minimum velocity (speed) necessary to achieve this range.

Answer

\(v=42.16\) m/sec

22. Prove that an object moving in a straight line at a constant speed has an acceleration of zero.

Exercises 23 - 31

Find the tangential and normal components of acceleration.

23. \(\mathbf r(t)=t^2\,\mathbf{i}+2t \,\mathbf{j}\) when \(t=1\).

Answer

\(a_\mathbf{T}=\sqrt{2}, \quad a_\mathbf{N}=\sqrt{2}\)

24. \(\mathbf r(t)=⟨\cos(2t),\,\sin(2t),1⟩\)
25. \(\mathbf r(t)=⟨e^t \cos t,\,e^t\sin t,\,e^t⟩\). The graph is shown here:

Figure \(\PageIndex{6}\): The graph of the given vector function is a curve that forms a smooth arc. The plot is enclosed within a rectangular box with the horizontal axis ranging from 0 to 1.5, the vertical axis ranging from 0 to 4, and the depth axis ranging from -0.5 to 5. The curve goes from lower-left front, rises slowly as it moves to the right, then left, ending in the upper-left back.

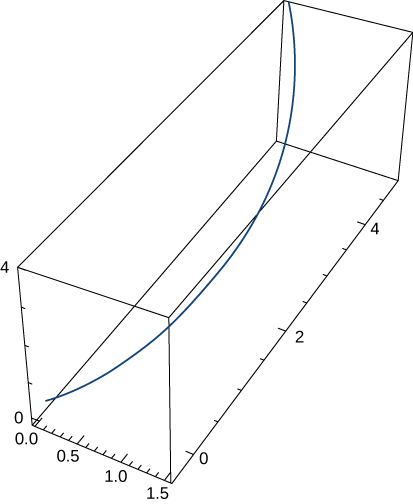
Answer

\(a_\mathbf{T}=\sqrt{3}e^t, \quad a_\mathbf{N}=\sqrt{2}e^t\)

26. \(\mathbf r(t)=⟨\frac{2}{3}(1+t)^{3/2}, \,\frac{2}{3}(1-t)^{3/2},\,\sqrt{2}t⟩\)
27. \(\mathbf r(t)=\left\langle 2t,\,t^2,\,\dfrac{t^3}{3}\right\rangle\)

Answer

\(a_\mathbf{T}=2t, \quad a_\mathbf{N}=2\)

28. \(\mathbf r(t)=t^2\,\mathbf{i}+t^2\,\mathbf{j}+t^3\,\mathbf{k}\)
29. \(\mathbf r(t)=⟨6t,\,3t^2,\,2t^3⟩\)

Answer

\(a_\mathbf{T}=\dfrac{6t +12t^3}{\sqrt{1+t^2+t^4}}, \quad a_\mathbf{N}=6\sqrt{\dfrac{1+4t^2+t^4}{1+t^2+t^4}}\)

30. \(\mathbf r(t)=3\cos(2πt)\,\mathbf{i}+3\sin(2πt)\,\mathbf{j}\)

Answer

\(a_\mathbf{T}=0, \quad a_\mathbf{N}=12\pi^2\)

31. \(\mathbf r(t)=a\cos(ωt)\,\mathbf{i}+b\sin(ωt)\,\mathbf{j}\) at \(t=0\).

Exercises 32 - 36

Answer

\(a_\mathbf{T}=0, \quad a_\mathbf{N}=aω^2\)

32. Suppose that the position function for an object in three dimensions is given by the equation \(\mathbf r(t)=t\cos(t)\,\mathbf{i}+t\sin(t)\,\mathbf{j}+3t\,\mathbf{k}\).

1. Show that the particle moves on a circular cone.
2. Find the angle between the velocity and acceleration vectors when \(t=1.5\).
3. Find the tangential and normal components of acceleration when \(t=1.5\).

Answer

3. \(a_\mathbf{T}=0.43\,\text{m/sec}^2, \quad a_\mathbf{N}=2.46\,\text{m/sec}^2\)

33. The force on a particle is given by \(\mathbf f(t)=(\cos t)\,\mathbf{i}+(\sin t)\,\mathbf{j}\). The particle is located at point \((c,0)\) at \(t=0\). The initial velocity of the particle is given by \(\mathbf v(0)=v_0\,\mathbf{j}\). Find the path of the particle of mass \(m\). (Recall, \(\mathbf F=m\mathbf a\).)

Answer

\(\mathbf r(t)=\left(\dfrac{-\cos t}{m}+c+\frac{1}{m}\right)\,\mathbf{i}+\left(\dfrac{−\sin t}{m}+\left(v_0+\frac{1}{m}\right)t\right)\,\mathbf{j}\)

34. An automobile that weighs \(2700\) lb makes a turn on a flat road while traveling at \(56\) ft/sec. If the radius of the turn is \(70\) ft, what is the required frictional force to keep the car from skidding?
35. Using Kepler’s laws, it can be shown that \(v_0=\sqrt{\dfrac{2GM}{r_0}}\) is the minimum speed needed when \(\theta=0\) so that an object will escape from the pull of a central force resulting from mass \(M\). Use this result to find the minimum speed when \(\theta=0\) for a space capsule to escape from the gravitational pull of Earth if the probe is at an altitude of \(300\) km above Earth’s surface.

Answer

\(10.94\) km/sec

36. Find the time in years it takes the dwarf planet Pluto to make one orbit about the Sun given that \(a=39.5\) A.U.

Contributors

• Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.