5.1: Area of a Rectangle
- Page ID
- 19648
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Outcomes
- Find the area of a rectangle.
- Find the height of a rectangle given that the area is equal to 1.
Rectangles are of fundamental importance in the portion of statistics that involves the uniform distribution. Every rectangle has a base and a height and an area. The formula for the area of a rectangle is:
\[\text{Area} = \text{Base} \times \text{Height} \label{AreaFormula} \]
When working with the uniform distribution, the area represents the probability of an event being within the bounds of the base.
Example \(\PageIndex{1}\)
Consider the rectangle shown below.
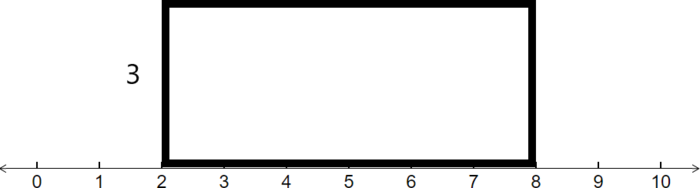
Find the area of this rectangle.
Solution
We use the Area formula (Equation \ref{AreaFormula}). To find the base, we notice that it runs from 2 to 8, so we subtract these numbers to get the base:
\[Base\:=\:8\:-\:2\:=\:6\nonumber \]
Next multiply by the height, 3, to get
\[Area\:=\:Base\:\times Height\:=\:6\:\times3\:=\:18\nonumber \]
Example \(\PageIndex{2}\)
It turns out that the area of the rectangles that equal to 1 will occur the most often for a uniform distribution. Suppose that we know that the area of a rectangle that depicts a uniform distribution is equal to 1 and that the base of the rectangle goes from 4 to 7. Find the height of the rectangle.
Solution
First sketch the rectangle below, labeling the height as \(h\).

Next, find the base of the rectangle that goes from 4 to 7 by subtracting:
\[Base\:=\:7-4=3\nonumber \]
Next, plug in what we know into the area equation:
\[1\:=\:Area\:=\:Base\:\times Height\:=\:3\times h\nonumber \]
This tell us that 3 times a number is equal to 1. To find out what the number is, we just divide both sides by 3 to get:
\[h=\frac{1}{3}\nonumber \]
Therefore the height of an area 1 rectangle with base from 4 to 7 is \(\frac{1}{3}\).
Example \(\PageIndex{3}\)
Suppose that we know that the area of a rectangle that depicts a uniform distribution is equal to 1 and that the base of the rectangle goes from 3 to 5. There is a smaller rectangle within the larger one with the same height, but whose base goes from 3.7 to 4.4. Find the area of the smaller rectangle.
Solution
First, sketch the larger rectangle with the smaller rectangle shaded in.
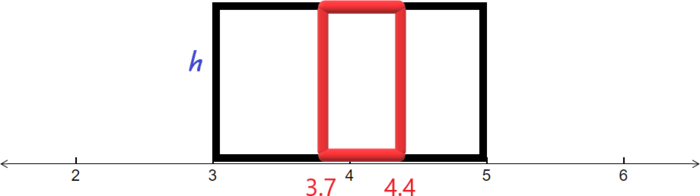
Next, we find the height of the rectangle. We know that the area of the larger rectangle is 1. The base goes from 3 to 5, so the base is \(5-3=2\) Hence:
\[1\:=\:Area\:=\:Base\:\times Height\:=\:2h\nonumber \]
Dividing by 2, gives us that the height is \(\frac{1}{2}\) or 0.5. Now we are ready to find the area of the smaller rectangle. We first find the base by subtracting:
\[\text{Base}\:=\:4.4-3.7\:=\:0.7\nonumber \]
Next, use the area formula:
\[Area\:=\:Base\:\times Height\:=\:0.7\:\times0.5\:=\:0.35\nonumber \]
Exercise \(\PageIndex{1}\)
Suppose that elementary students' ages are uniformly distributed from 5 to 11 years old. The rectangle that depicts this has base from 5 to 11 and area 1. The rectangle that depicts the probability that a randomly selected child will be between 6.5 and 8.6 years old has base from 6.5 to 8.6 and the same height as the larger rectangle. Find the area of the smaller rectangle


