3.7: Transformations of Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Identify transformations of functions.
- Graph functions using transformations.
- Find functions that model transformed graphs.
- Determine whether a function is even, odd, or neither from its graph.
Try these questions prior to beginning this section to help determine if you are set up for success:
- Simplify the given expression:
- √50
- 2−√124
- Determine the value of k that will make the trinomial a perfect square: x2+6x+k
- Solve:
- x2+4x=6
- (y−5)2−18=0
- √1−5a−3=0
- Answer
-
-
- 5√2
- 12−√32
If you missed this problem or feel you could use more practice, review [2.18: Simplifying Radical Expressions]
- k=9
If you missed this problem or feel you could use more practice, review [2.25: Solving Quadratic Equations by Completing the Square]
-
- −2±√10
- 5±3√2
- −85
If you missed this problem or feel you could use more practice, review [2.24: Solving Quadratic Equations Using the Square Root Property, 2.25: Solving Quadratic Equations by Completing the Square, 2.26: Solving Quadratic Equations Using the Quadratic Formula, and 2.22: Solving Radical Equations]
-
We all know that a flat mirror enables us to see an accurate image of ourselves and whatever is behind us. When we tilt the mirror, the images we see may shift horizontally or vertically. But what happens when we bend a flexible mirror? Like a carnival funhouse mirror, it presents us with a distorted image of ourselves, stretched or compressed horizontally or vertically. In a similar way, we can distort or transform mathematical functions to better adapt them to describing objects or processes in the real world. In this section, we will take a look at several kinds of transformations.

Often when given a problem, we try to model the scenario using mathematics in the form of words, tables, graphs, and equations. One method we can employ is to adapt the basic graphs of the basic functions to build new models for a given scenario. There are systematic ways to alter functions to construct appropriate models for the problems we are trying to solve.
Identifying Vertical Shifts
One simple kind of transformation involves shifting the entire graph of a function up, down, right, or left. The simplest shift is a vertical shift, moving the graph up or down, because this transformation involves adding a positive or negative constant to the function. In other words, we add the same constant to the output value of the function regardless of the input. For a function g(x)=f(x)+c, the function f(x) is shifted vertically c units. See Figure 3.7.2 for an example.
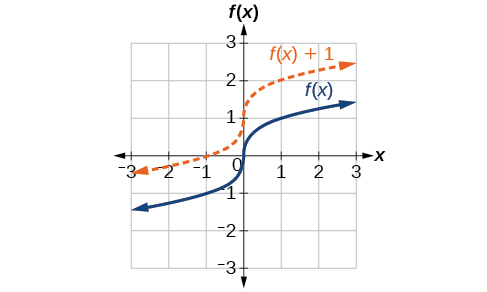
To help you visualize the concept of a vertical shift, consider that y=f(x). Therefore, f(x)+c is equivalent to y+c. Every unit of y is replaced by y+c, so the y-value increases or decreases depending on the value of c. The result is a shift upward or downward.
Given a function f(x), a new function g(x)=f(x)+c, where c is a constant, is a vertical shift of the function f(x). All the output values change by c units. If c is positive, the graph will shift up. If c is negative, the graph will shift down.
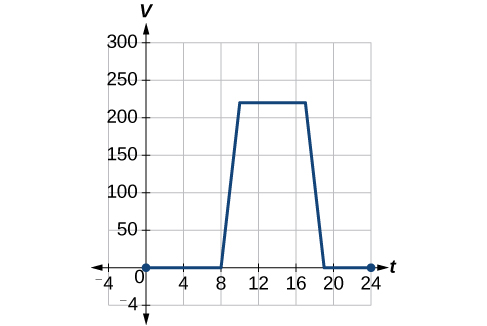
To regulate temperature in a green building, airflow vents near the roof open and close throughout the day. Figure 3.7.3 shows the area of open vents V (in square feet) throughout the day in hours after midnight, t. During the summer, the facilities manager decides to try to better regulate temperature by increasing the amount of open vents by 20 square feet throughout the day and night. Sketch a graph of this new function.
Solution
We can sketch a graph of this new function by adding 20 to each of the output values of the original function. This will have the effect of shifting the graph vertically up, as shown in Figure 3.7.4.
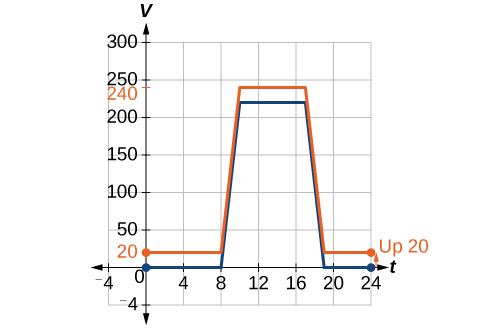
Notice that in Figure 3.7.4, for each input value, the output value has increased by 20, so if we call the new function S(t),we could write
S(t)=V(t)+20
This notation tells us that, for any value of t,S(t) can be found by evaluating the function V at the same input and then adding 20 to the result. This defines S as a transformation of the function V, in this case a vertical shift up 20 units. Notice that, with a vertical shift, the input values stay the same and only the output values change. See Table 3.7.1.
| t | 0 | 8 | 10 | 17 | 19 | 24 |
|---|---|---|---|---|---|---|
| V(t) | 0 | 0 | 220 | 220 | 0 | 0 |
| S(t) | 20 | 20 | 240 | 240 | 20 | 20 |
Identifying Horizontal Shifts
We just saw that the vertical shift is a change to the output, or outside, of the function. We will now look at how changes to input, on the inside of the function, change its graph and meaning. A shift to the input results in a movement of the graph of the function left or right in what is known as a horizontal shift, shown in Figure 3.7.5.
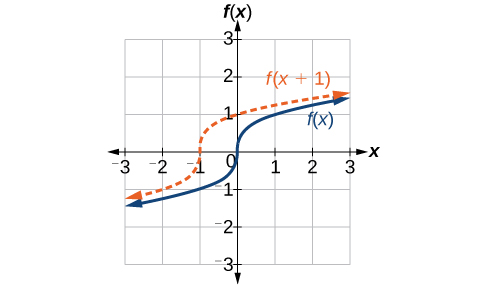
For example, if f(x)=x2, then g(x)=(x−2)2 is a new function. Each input is reduced by 2 prior to squaring the function. The result is that the graph is shifted 2 units to the right, because we would need to increase the prior input by 2 units to yield the same output value as given in f.
Given a function f, a new function g(x)=f(x−c), where c is a constant, is a horizontal shift of the function f. If c is positive, the graph will shift right. If c is negative, the graph will shift left.
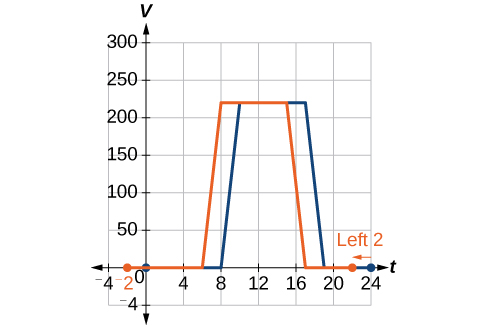
Returning to our building airflow example from Figure 3.7.3, suppose that in autumn the facilities manager decides that the original venting plan starts too late, and wants to begin the entire venting program 2 hours earlier. Sketch a graph of the new function.
Solution
We can set V(t) to be the original program and F(t) to be the revised program.
V(t)= the original venting plan
F(t)= starting 2 hrs sooner
In the new graph, at each time, the airflow is the same as the original function V was 2 hours later. For example, in the original function V, the airflow starts to change at 8 a.m., whereas for the function F, the airflow starts to change at 6 a.m. The comparable function values are V(8)=F(6). See Figure 3.7.6. Notice also that the vents first opened to 220ft2 at 10 a.m. under the original plan, while under the new plan the vents reach 220ft2 at 8 a.m., so V(10)=F(8).
In both cases, we see that, because F(t) starts 2 hours sooner, c=−2. That means that the same output values are reached when F(t)=V(t−(−2))=V(t+2).
Analysis
Note that V(t+2) has the effect of shifting the graph to the left.
Horizontal changes or “inside changes” affect the domain of a function (the input) instead of the range and often seem counterintuitive. The new function F(t) uses the same outputs as V(t), but matches those outputs to inputs 2 hours earlier than those of V(t). Said another way, we must add 2 hours to the input of V to find the corresponding output for F:F(t)=V(t+2).
Notice that, with a vertical shift, the input values stay the same and only the output values change. See Table 3.7.2.
| t | 0 | 8 | 10 | 17 | 19 | 24 |
|---|---|---|---|---|---|---|
| t+2 | -2 | 6 | 8 | 15 | 17 | 22 |
| V(t) | 0 | 0 | 220 | 220 | 0 | 0 |
| S(t) | 0 | 0 | 220 | 220 | 0 | 0 |
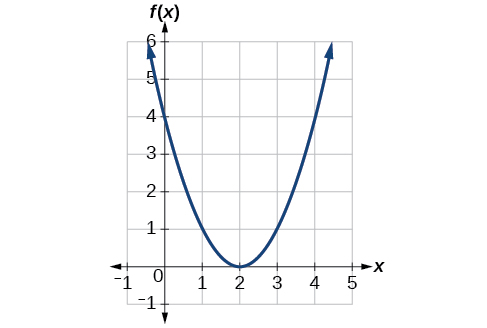
A graph of f(x) is shown in Figure 3.7.7 which represents a transformation of the basic function y=x2. Find an equation for f(x).
Solution
Notice that the graph is identical in shape to the f(x)=x2 function, but the x-values are shifted to the right 2 units. The vertex used to be at (0,0), but now the vertex is at (2,0). The graph is the basic quadratic function shifted 2 units to the right, so
g(x)=f(x−2)
Notice how we must input the value x=2 to get the output value y=0; the x-values must be 2 units larger because of the shift to the right by 2 units. We can then use the definition of the f(x) function to write a formula for g(x) by evaluating f(x−2).
f(x)=x2g(x)=f(x−2)g(x)=f(x−2)=(x−2)2
Analysis
To determine whether the shift is +2 or −2, consider a single reference point on the graph. For a quadratic, looking at the vertex point is convenient. In the original function, f(0)=0. In our shifted function, g(2)=0. To obtain the output value of 0 from the function f, we need to decide whether a plus or a minus sign will work to satisfy g(2)=f(x−2)=f(0)=0. For this to work, we will need to subtract 2 units from our input values.
The function G(m) gives the number of gallons of gas required to drive m miles. Interpret G(m)+10 and G(m+10)
Solution
G(m)+10 can be interpreted as adding 10 to the output, gallons. This is the gas required to drive m miles, plus another 10 gallons of gas. The graph would indicate a vertical shift.
G(m+10) can be interpreted as adding 10 to the input, miles. So this is the number of gallons of gas required to drive 10 miles more than m miles. The graph would indicate a horizontal shift.
You Try 3.7.1
Given the function f(x)=√x, graph the original function f(x) and the transformation g(x)=f(x+2) on the same axes. Is this a horizontal or a vertical shift? Which way is the graph shifted and by how many units?
- Answer
-
The graphs of f(x) and g(x) are shown below. The transformation is a horizontal shift. The function is shifted to the left by 2 units.
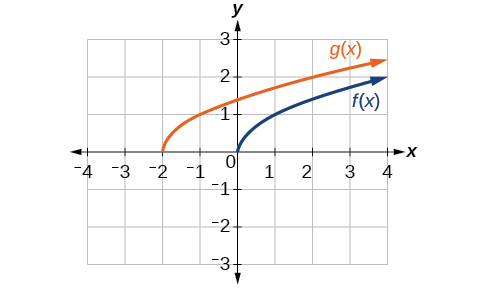
Figure 3.7.8
Combining Vertical and Horizontal Shifts
Now that we have two transformations, we can combine them together. Vertical shifts are outside changes that affect the y-coordinates of points and shift the function up or down. Horizontal shifts are inside changes that affect the x-coordinates of points and shift the function left or right. Combining the two types of shifts will cause the graph of a function to shift up or down and right or left.
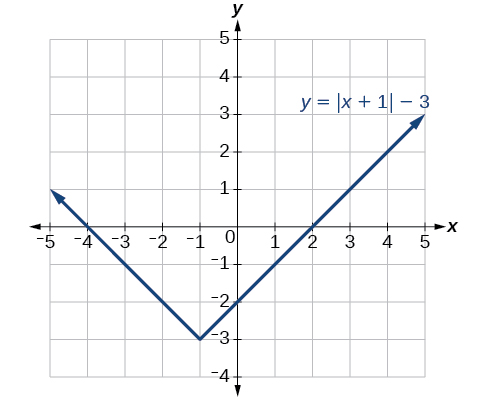
Given f(x)=|x|, sketch a graph of h(x)=f(x+1)−3.
Solution
The function f is our basic absolute value function. We know that this graph has a V shape, with the point at the origin. The graph of h has transformed f in two ways: f(x+1) is a change on the inside of the function, giving a horizontal shift left by 1, and the subtraction by 3 in f(x+1)−3 is a change to the outside of the function, giving a vertical shift down by 3. The transformation of the graph is illustrated in Figure 3.7.9.
Let us follow one point of the graph of f(x)=|x|.
- The point (0,0) is transformed first by shifting left 1 unit:(0,0)→(−1,0)
- The point (−1,0) is transformed next by shifting down 3 units:(−1,0)→(−1,−3)
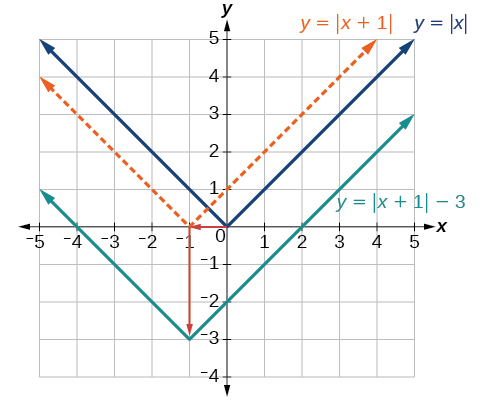
Figure 3.7.10 shows the graph of h.
Given f(x)=|x|, sketch a graph of h(x)=f(x−2)+4.
- Answer
-
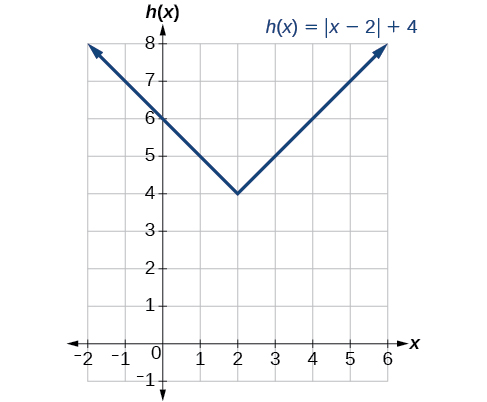
Figure 3.7.11
Write an equation for the function, h(x) that models the graph shown in Figure 3.7.12, which is a transformation of the basic square root function.
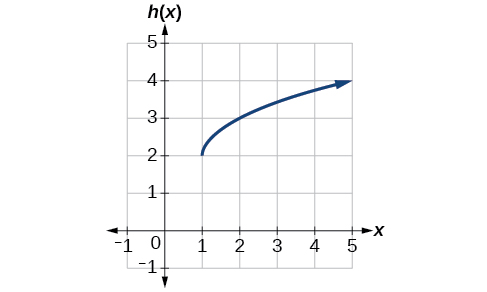
Solution
The graph of the basic function starts at the origin, so this graph has been shifted 1 to the right and up 2. In function notation, we could write that as
h(x)=f(x−1)+2
Using the formula for the square root function, we can write
h(x)=√x−1+2
Analysis
Note that this transformation has changed the domain and range of the function. This new graph has domain [1,∞) and range [2,∞).
Graphing Functions Using Reflections about the Axes
Another transformation that can be applied to a function is a reflection over the x- or y-axis. A vertical reflection reflects a graph vertically across the x-axis, while a horizontal reflection reflects a graph horizontally across the y-axis. The reflections are shown in Figure 3.7.13.
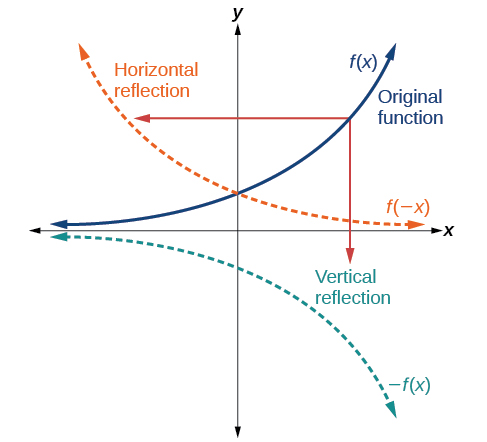 .
.
Notice that the vertical reflection produces a new graph that is a mirror image of the base or original graph about the x-axis. As a result, vertical reflections are also called x-axis reflections. The horizontal reflection produces a new graph that is a mirror image of the base or original graph about the y-axis. As a result, horizontal reflections are also called y-axis reflections.
Given a function f(x), a new function g(x)=−f(x) is a vertical reflection of the function f(x), sometimes called a reflection about (or over, or through) the x-axis.
Given a function f(x), a new function g(x)=f(−x) is a horizontal reflection of the function f(x), sometimes called a reflection about the y-axis.
Reflect the graph of s(t)=√t (a) vertically and (b) horizontally.
Solution
a. Reflecting the graph vertically means that each output value will be reflected over the horizontal t-axis as shown in Figure 3.7.14.
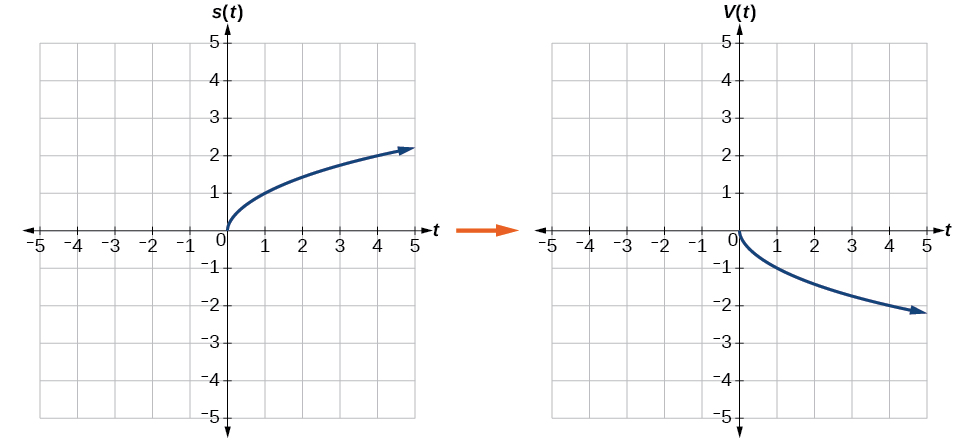
Because each output value is the opposite of the original output value, we can write
V(t)=−s(t) or V(t)=−√t
Notice that this is an outside change, or vertical shift, that affects the output s(t) values, so the negative sign belongs outside of the function.
b. Reflecting horizontally means that each input value will be reflected over the vertical axis as shown in Figure 3.7.15.
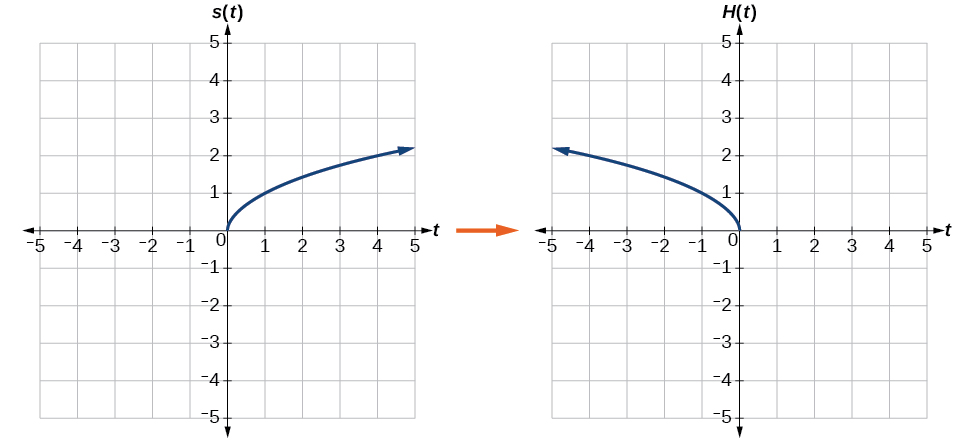
Because each input value is the opposite of the original input value, we can write
H(t)=s(−t) or H(t)=√−t
Notice that this is an inside change or horizontal change that affects the input values, so the negative sign is on the inside of the function.
Note that these transformations can affect the domain and range of the functions. While the original square root function has domain [0,∞) and range [0,∞), the vertical reflection gives the V(t) function the range (−∞,0] and the horizontal reflection gives the H(t) function the domain (−∞,0].
You Try 3.7.3
Reflect the graph of f(x)=|x−1| (a) vertically and (b) horizontally.
- Answer
-
a.
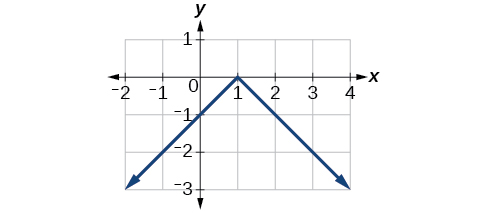
Figure 3.7.16: Graph of a vertically reflected absolute function. The function that describes this graph is g(x)=−|x−1|
b.
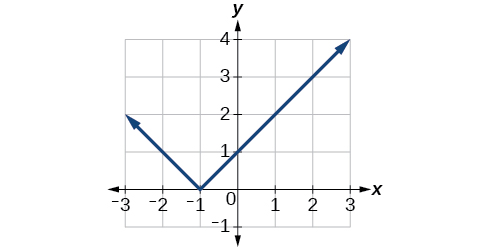
Figure 3.7.17: Graph of an absolute function translated one unit left. The function that describes this graph is h(x)=|−(x+1)| or h(x)=|−x−1|
A function f(x) is given as Table 3.7.3. Create a table for the functions below.
a. g(x)=−f(x)
b. h(x)=f(−x)
| x | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| f(x) | 1 | 3 | 7 | 11 |
a. For g(x), the negative sign outside the function indicates a vertical reflection, so the x-values stay the same and each output value will be the opposite of the original output value. See Table 3.7.4.
| x | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| g(x) | -1 | -3 | -7 | -11 |
b. For h(x), the negative sign inside the function indicates a horizontal reflection, so each input value will be the opposite of the original input value and the h(x) values stay the same as the f(x) values. See Table 3.7.5.
| x | -2 | -4 | -6 | -8 |
|---|---|---|---|---|
| h(x) | 1 | 3 | 7 | 11 |
You Try 3.7.4
Given the basic function f(x)=x2, graph g(x)=−f(x) and h(x)=f(−x).
- Answer
-
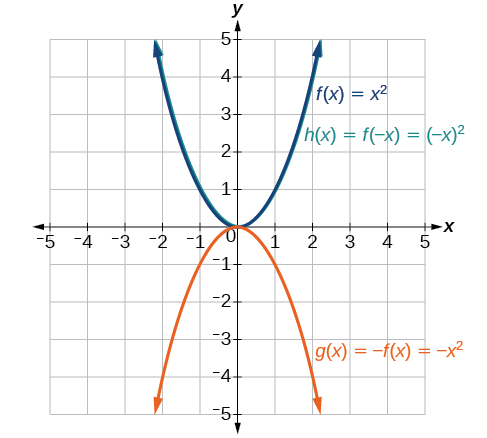
Figure 3.7.18: Graph of x2 and its reflections. Notice: g(x)=f(−x) looks the same as f(x).
Graphing Functions Using Stretches and Compressions
Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect the shape of a graph. We now explore the effects of multiplying the inputs or outputs by some quantity.
We can transform the inside (input values) of a function or we can transform the outside (output values) of a function. Each change has a specific effect that can be seen graphically.
Vertical Stretches and Compressions
When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. If the constant is greater than 1, we get a vertical stretch; if the constant is between 0 and 1, we get a vertical compression. Figure 3.7.19 shows a function multiplied by constant factors 2 and 0.5 and the resulting vertical stretch and compression.
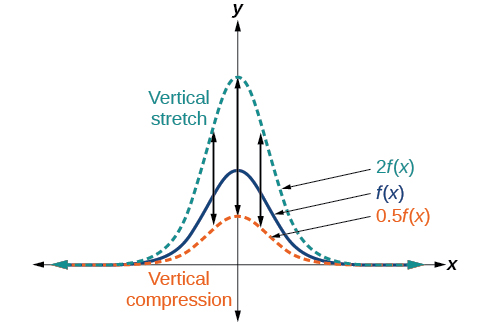
Given a function f(x), a new function g(x)=af(x), where a is a constant, is a vertical stretch or vertical compression of the function f(x).
- If a>1, then the graph will be stretched vertically.
- If 0<a<1, then the graph will be compressed vertically.
- If a<0, then there will be combination of a vertical stretch or compression with a vertical reflection.
A function P(t) models the population of fruit flies. The graph is shown in Figure 3.7.20.
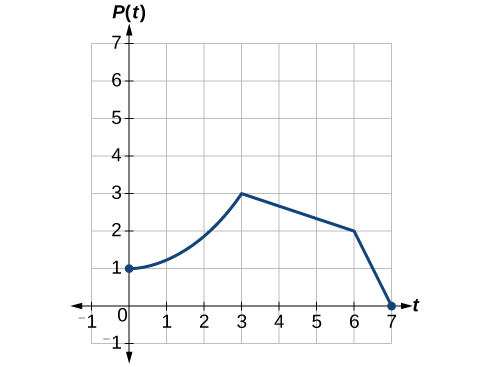
A scientist is comparing this population to another population, Q, whose growth follows the same pattern, but is twice as large. Sketch a graph of this population.
Solution
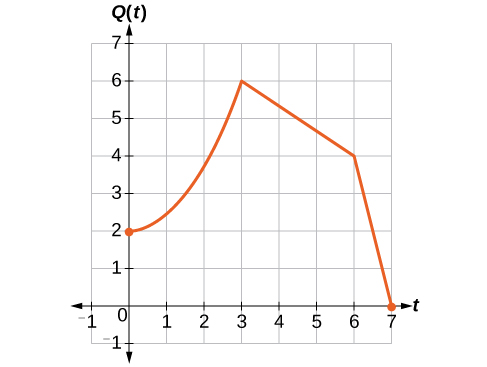
Because the population is always twice as large, the new population’s output values are always twice the original function’s output values. Graphically, this is shown in Figure 3.7.21.
If we choose four reference points, (0,1), (3,3), (6,2) and (7,0) we will multiply all of the outputs by 2.
The following shows where the new points for the new graph will be located.
(0,1)→(0,2)
(3,3)→(3,6)
(6,2)→(6,4)
(7,0)→(7,0)
Symbolically, the relationship is written as
Q(t)=2P(t)
This means that for any input t, the value of the function Q is twice the value of the function P. Notice that the effect on the graph is a vertical stretching of the graph, where every point doubles its distance from the horizontal axis. The input values, t, stay the same while the output values are twice as large as before.
Write an equation for the function, g(x) that models the graph shown in Figure 3.7.22, which is a transformation of the basic cubic function.
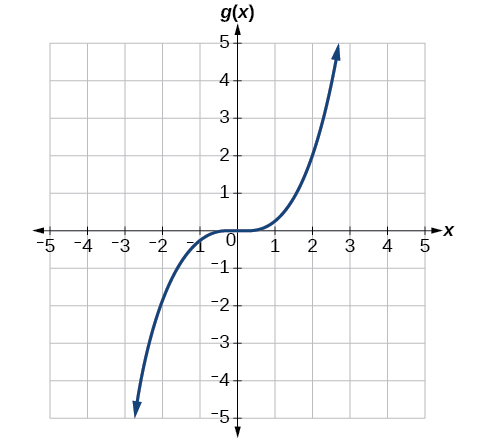
When trying to determine a vertical stretch or shift, it is helpful to look for a point on the graph that is relatively clear. In this graph, it appears that g(2)=2. With the basic cubic function at the same input, f(2)=23=8. Based on that, it appears that the outputs of g are 14 the outputs of the function f because g(2)=14f(2). From this we can fairly safely conclude that g(x)=14f(x).
We can write a formula for g by using the definition of the function f.
g(x)=14f(x)=14x3.
You Try 3.7.5
Write an equation for a function that is a stretch of the basic cubic function vertically by a factor of 4, shifted right 5 units, and then shifted down by 2 units.
- Answer
-
g(x)=4(x−5)3−2
Horizontal Stretches and Compressions
Now we consider changes to the inside of a function. When we multiply a function’s input by a positive constant, we get a function whose graph is stretched or compressed horizontally in relation to the graph of the original function. If the constant is between 0 and 1, we get a horizontal stretch; if the constant is greater than 1, we get a horizontal compression of the function.
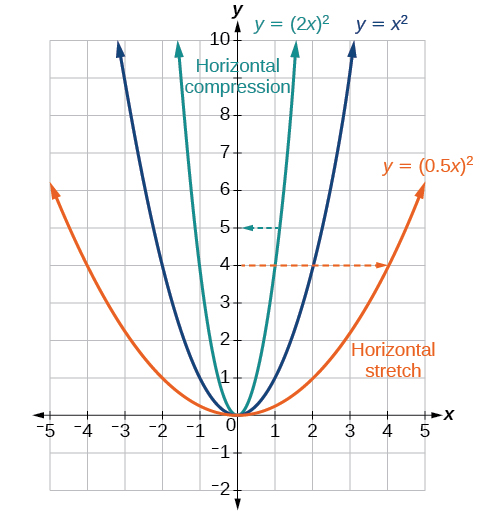
Given a function y=f(x), the form y=f(bx) results in a horizontal stretch or compression. Consider the function y=x2. Observe Figure 3.7.23. The graph of y=(0.5x)2 is a horizontal stretch of the graph of the function y=x2 by a factor of 2. The graph of y=(2x)2 is a horizontal compression of the graph of the function y=x2 by a factor of 2.
Given a function f(x), a new function g(x)=f(bx), where b is a constant, is a horizontal stretch or horizontal compression of the function f(x).
- If b>1, then the graph will be compressed horizontally by 1b.
- If 0<b<1, then the graph will be stretched horizontally by 1b.
- If b<0, then there will be combination of a horizontal stretch or compression with a horizontal reflection.
Suppose a scientist is comparing a population of fruit flies to a population that progresses through its lifespan twice as fast as the original population. In other words, this new population, R, will progress in 1 hour the same amount as the original population does in 2 hours, and in 2 hours, it will progress as much as the original population does in 4 hours. Sketch a graph of this population.
Solution
Symbolically, we could write
R(1)=P(2),R(2)=P(4),and in general,R(t)=P(2t).
See Figure 3.7.24 for a graphical comparison of the original population and the compressed population.
![Two side-by-side graphs. The first graph has function for original population whose domain is [0,7] and range is [0,3]. The maximum value occurs at (3,3). The second graph has the same shape as the first except it is half as wide. It is a graph of transformed population, with a domain of [0, 3.5] and a range of [0,3]. The maximum occurs at (1.5, 3).](https://math.libretexts.org/@api/deki/files/995/CNX_Precalc_Figure_01_05_029ab.jpg?revision=1)
Analysis
Note that the effect on the graph is a horizontal compression where all input values are half of their original distance from the vertical axis.
Use transformations to describe the function g(x) in terms of f(x) in Figure 3.7.25.
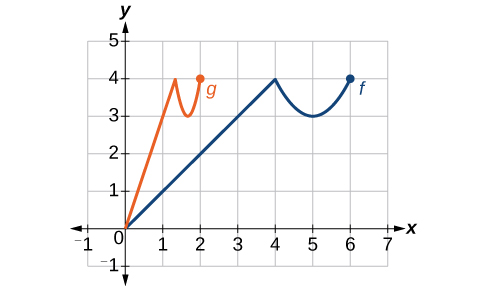
Solution
The graph of g(x) looks like the graph of f(x) horizontally compressed. Because f(x) ends at (6,4) and g(x) ends at (2,4), we can see that the x-values have been compressed by 13, because 6(13)=2. We might also notice that g(2)=f(6) and g(1)=f(3). Either way, we can describe this relationship as g(x)=f(3x). This is a horizontal compression by 13.
Analysis
Notice that the coefficient needed for a horizontal stretch or compression is the reciprocal of the stretch or compression. So to stretch the graph horizontally by a scale factor of 4, we need a coefficient of 14 in our function: f(14x). This means that the input values must be four times larger to produce the same result, requiring the input to be larger, causing the horizontal stretching.
You Try 3.7.6
Write a formula for the basic square root function horizontally stretched by a factor of 3.
- Answer
-
g(x)=f(13x), so using the square root function we get g(x)=√13x
Performing a Sequence of Transformations
When combining transformations, it is very important to consider the order of the transformations. For example, vertically shifting by 3 and then vertically stretching by 2 does not create the same graph as vertically stretching by 2 and then vertically shifting by 3, because when we shift first, both the original function and the shift get stretched, while only the original function gets stretched when we stretch first.
When we see an expression such as 2f(x)+3, which transformation should we start with? The answer here follows nicely from the order of operations. Given the output value of f(x), we first multiply by 2, causing the vertical stretch, and then add 3, causing the vertical shift. In other words, multiplication before addition.
Horizontal transformations are a little trickier to think about sometimes. When we write g(x)=f(2x+6), for example, we have to think about how the inputs to the function g relate to the inputs to the function f. A way to identify the transformations is to factor inside the functionfirst to rewrite the function in a form that we can identify all the transformations, g(x)=f(2x+6)=f(2(x+3). Function g(x) is a horizontal compression of f(x) by 2 and a horizontal shifting of f(x) to the left by 3.
Let’s work through an example.
f(x)=(3x−12)2
We can factor out a 3.
f(x)=(3(x−4))2
Now we can more clearly observe a horizontal shift to the right 4 units and a horizontal compression by 3. Factoring in this way allows us to horizontally compress first and then shift horizontally.
- When combining vertical transformations written in the form af(x)+k, first vertically stretch by a and then vertically shift by k.
- When combining horizontal transformations written in the form f(b(x+h)), first horizontally stretch by 1b and then horizontally shift by h. If b<0 there is also a horizontal reflection over the y-axis.
- When combining horizontal transformations written in the form f(b(x+h)), first horizontally stretch by 1b and then horizontally shift by h. If b<0 there is also a horizontal reflection over the y-axis.
- Horizontal and vertical transformations are independent. It does not matter whether horizontal or vertical reflections are performed first.
Use the graph of f(x) in Figure 3.7.26 to sketch a graph of k(x)=f(12x+1)−3.
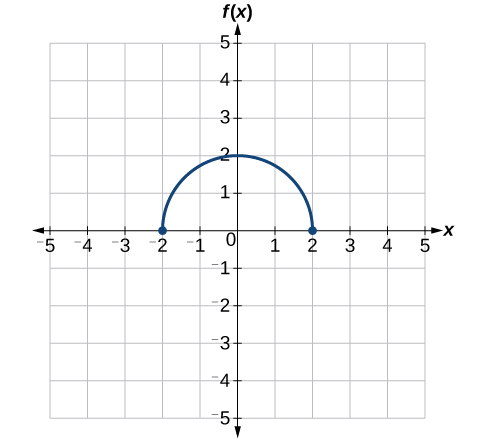
To simplify, let’s start by factoring out the inside of the function.
f(12x+1)−3=f(12(x+2))−3
By factoring the inside, we can first horizontally stretch by 2, as indicated by the 12 on the inside of the function. Remember that twice the size of 0 is still 0, so the point (0,2) remains at (0,2) while the point (2,0) will stretch to (4,0). See Figure 3.7.27.
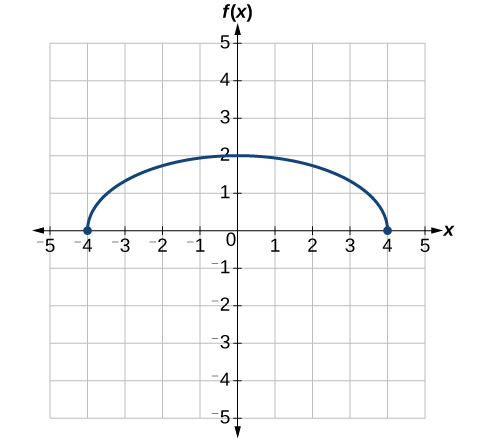
Next, we horizontally shift left by 2 units, as indicated by x+2. See Figure 3.7.28.
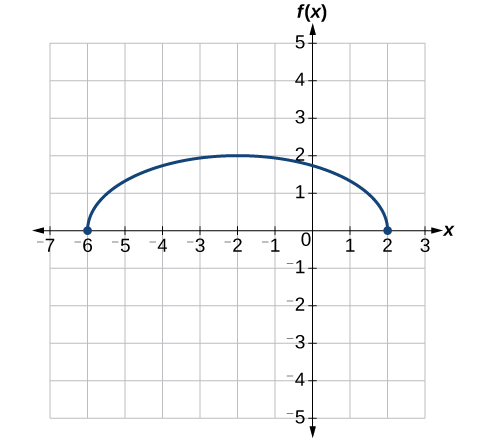
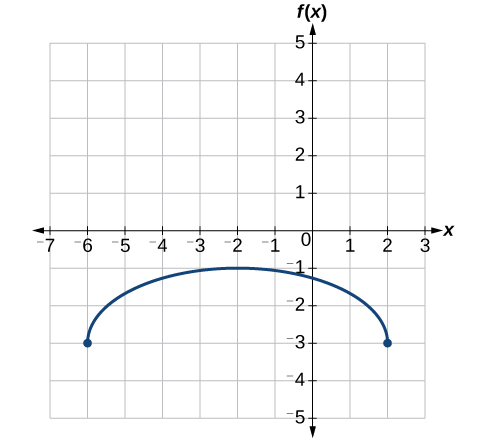
Last, we vertically shift down by 3 to complete our sketch, as indicated by the −3 on the outside of the function. See Figure 3.7.29.
Given the function r(x)=√x−3−5,
- Identify the transformations and use them to sketch the graph.
- Based on what you found in part 1, how many x-intercepts do you expect there to be for this function? Explain.
- Find the x-intercept(s) of r(x).
Solution
- The basic function shifts right 3 units and down 5 units.
_transformations.png?revision=1&size=bestfit&width=414&height=414)
- It is expected that there is one x-intercept based on the transformations and the shape of the square root function. The x-intercept should have a fairly large x-coordinate, likely larger than 10, since this square root function increases fairly slowly.
- Solving for the x-intercept: 0=√x−3−55=√x−3(5)2=(√x−3)225=x−328=xThe x-intercept is (28,0).
Given the function p(x)=−5(x−4)2+2,
- Identify the transformations and use them to sketch the graph.
- Based on what you found in part 1, how many x-intercepts do you expect there to be for this function? Explain.
- Now, use your knowledge of solving equations to find the x-intercept(s) of p(x) algebraically, if they exist.
Solution
- The basic function shifts right 4 units and up 2 units. There is an x-axis reflection and a vertical stretch by 5.
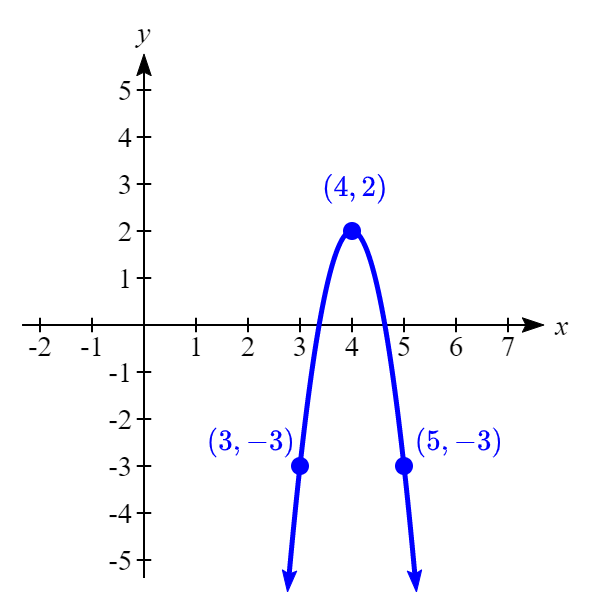.png?revision=1&size=bestfit&width=414&height=415)
- Based on the transformations and shape of the basic graph, it is expected that there should be two x-intercepts with x-coordinates within the intervals (3,4) and (4,5).
- Solving for the x-intercepts: 0=−5(x−4)2+2−2=−5(x−4)225=(x−4)2±√25=√(x−4)2±√25=x−44±√25=xThe x-intercepts are (4−√25,0) and (4+√25,0).
Note: (4−√25,0)≈(3.37,0) and (4+√25,0)≈(4.63,0) which follows what was expected visually.
Given the function k(x)=4(x+2)3−3:
- Based on your knowledge of transformations, how many x-intercepts do you expect to have and where do you anticipate the x-intercept(s) to be within the coordinate system? Explain.
- Now, use your knowledge of solving equations to find the x-intercept(s) of k(x)algebraically, if they exist.
- Answer
-
- This is a cubic function with a vertical stretch by 4 with a horizontal shift left 2 units and vertical shift down 3 units. Based on this knowledge, there should be one x-intercept with a x-coordinate within the interval (−2,−1).
- The x-intercept is (−2+3√34,0).
Determining Even and Odd Functions
Some functions exhibit symmetry so that reflections result in the original graph. For example, horizontally reflecting the basic functions f(x)=x2 or f(x)=|x| will result in the original graph. We say that these types of graphs are symmetric about the y-axis. Functions whose graphs are symmetric about the y-axis are called even functions.
If the graphs of f(x)=x3 or f(x)=1x were reflected over both axes, the result would be the original graph, as shown in Figure 3.7.32.
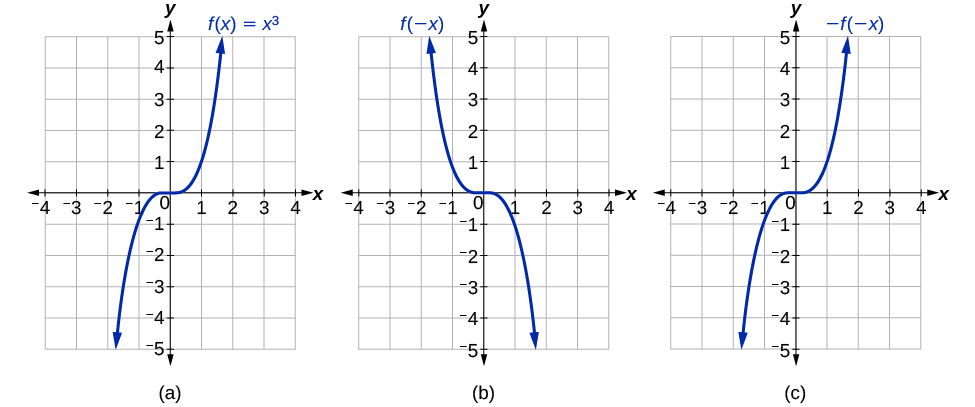
We say that these graphs are symmetric about the origin. A function with a graph that is symmetric about the origin is called an odd function.
Note: A function can be neither even nor odd if it does not exhibit either symmetry. For example, f(x)=2x is neither even nor odd. Also, the only function that is both even and odd is the constant function f(x)=0.
A function is called an even function if for every input x
f(x)=f(−x)
The graph of an even function is symmetric about the y-axis.
A function is called an odd function if for every input x
f(x)=−f(−x)
The graph of an odd function is symmetric about the origin.
Is the function f(x)=x3+2x even, odd, or neither?
Solution
Without looking at a graph, we can determine whether the function is even or odd by finding formulas for the reflections and determining if they return us to the original function. Let’s begin with the rule for even functions.
f(−x)=(−x)3+2(−x)=−x3−2x
This does not return us to the original function, so this function is not even. We can now test the rule for odd functions.
−f(−x)=−(−x3−2x)=x3+2x
Because −f(−x)=f(x), this is an odd function.
Analysis
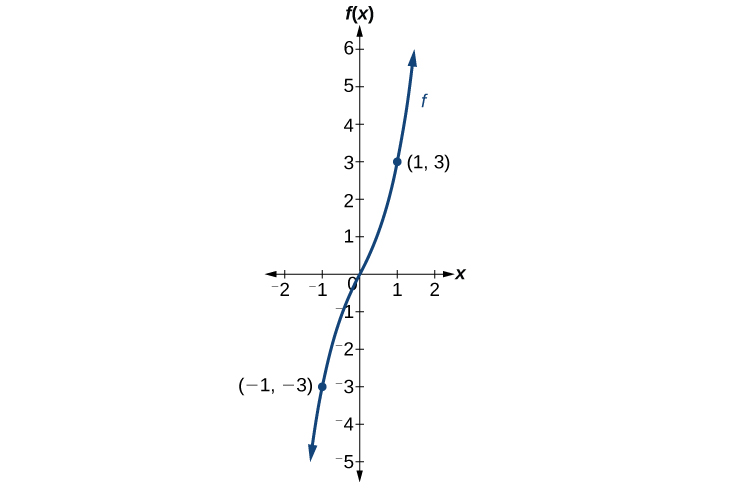
Consider the graph of f in Figure 3.7.33. Notice that the graph is symmetric about the origin. For every point (x,y) on the graph, the corresponding point (−x,−y) is also on the graph. For example, (1,3) is on the graph of f, and the corresponding point (−1,−3) is also on the graph.
You Try 3.7.8
Is the function f(s)=s4+3s2+7 even, odd, or neither?
- Answer
-
even
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


