1.6: Visualize Fractions
- Last updated
- May 3, 2019
- Save as PDF
- Page ID
- 18925
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Find equivalent fractions
- Simplify fractions
- Multiply fractions
- Divide fractions
- Simplify expressions written with a fraction bar
- Translate phrases to expressions with fractions
Note
A more thorough introduction to the topics covered in this section can be found in the Prealgebra chapter, Fractions.
Find Equivalent Fractions
Fractions are a way to represent parts of a whole. The fraction 13 means that one whole has been divided into 3 equal parts and each part is one of the three equal parts. See Figure 1.6.1. The fraction 23 represents two of three equal parts. In the fraction 23, the 2 is called the numerator and the 3 is called the denominator.
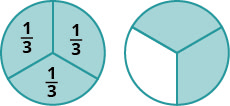
Doing the Manipulative Mathematics activity “Model Fractions” will help you develop a better understanding of fractions, their numerators and denominators.
FRACTION
A fraction is written ab, where b≠0 and
- a is the numerator and b is the denominator.
A fraction represents parts of a whole. The denominator b is the number of equal parts the whole has been divided into, and the numerator a indicates how many parts are included.
If a whole pie has been cut into 6 pieces and we eat all 6 pieces, we ate 66 pieces, or, in other words, one whole pie.
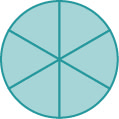
So 66=1. This leads us to the property of one that tells us that any number, except zero, divided by itself is 1.
PROPERTY OF ONE
aa=1(a≠0)
Any number, except zero, divided by itself is one.
Note
Doing the Manipulative Mathematics activity “Fractions Equivalent to One” will help you develop a better understanding of fractions that are equivalent to one.
If a pie was cut in 6 pieces and we ate all 6, we ate 66 pieces, or, in other words, one whole pie. If the pie was cut into 8 pieces and we ate all 8, we ate 88 pieces, or one whole pie. We ate the same amount—one whole pie.
The fractions 66 and 88 have the same value, 1, and so they are called equivalent fractions. Equivalent fractions are fractions that have the same value.
Let’s think of pizzas this time. Figure 1.6.3 shows two images: a single pizza on the left, cut into two equal pieces, and a second pizza of the same size, cut into eight pieces on the right. This is a way to show that 12 is equivalent to 48. In other words, they are equivalent fractions.
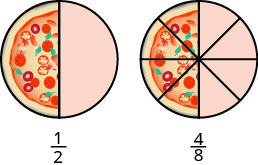
EQUIVALENT FRACTIONS
Equivalent fractions are fractions that have the same value.
How can we use mathematics to change 12 into 48? How could we take a pizza that is cut into 2 pieces and cut it into 8 pieces? We could cut each of the 2 larger pieces into 4 smaller pieces! The whole pizza would then be cut into 88 pieces instead of just 2. Mathematically, what we’ve described could be written like this as 1⋅42⋅4=48. See Figure 1.6.4.
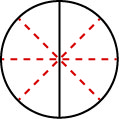
This model leads to the following property:
EQUIVALENT FRACTIONS PROPERTY
If a,b,c are numbers where b≠0,c≠0, then
ab=a⋅cb⋅c
If we had cut the pizza differently, we could get
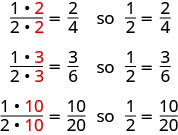
So, we say 12, 24, 36, and 1020 are equivalent fractions.
Note
Doing the Manipulative Mathematics activity “Equivalent Fractions” will help you develop a better understanding of what it means when two fractions are equivalent.
Example 1.6.1
Find three fractions equivalent to 25.
Solution
To find a fraction equivalent to 25, we multiply the numerator and denominator by the same number. We can choose any number, except for zero. Let’s multiply them by 2, 3, and then 5.
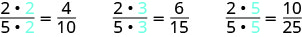
So, 410, 615, and 1025 are equivalent to 25.
Try It 1.6.2
Find three fractions equivalent to 35.
- Answer
-
610, 915, 1220; answers may vary
Try It 1.6.3
Find three fractions equivalent to 45.
- Answer
-
810, 1215, 1620; answers may vary
Simplify Fractions
A fraction is considered simplified if there are no common factors, other than 1, in its numerator and denominator.
For example,
- 23 is simplified because there are no common factors of 2 and 3.
- 1015 is not simplified because 5 is a common factor of 10 and 15.
SIMPLIFIED FRACTION
A fraction is considered simplified if there are no common factors in its numerator and denominator.
The phrase reduce a fraction means to simplify the fraction. We simplify, or reduce, a fraction by removing the common factors of the numerator and denominator. A fraction is not simplified until all common factors have been removed. If an expression has fractions, it is not completely simplified until the fractions are simplified.
In Exercise 1.6.4, we used the equivalent fractions property to find equivalent fractions. Now we’ll use the equivalent fractions property in reverse to simplify fractions. We can rewrite the property to show both forms together.
EQUIVALENT FRACTIONS PROPERTY
If a,b,c are numbers where b≠0,c≠0,
then ab=a⋅cb⋅c and a⋅cb⋅c=ab
Example 1.6.4
Simplify: −3256
Solution
| −3256 | |
| Rewrite the numerator and denominator showing the common factors. | −4⋅87⋅8 |
| Simplify using the equivalent fractions property. | −47 |
Notice that the fraction −47 is simplified because there are no more common factors.
pTry It 1.6.5
Simplify: −4254
- Answer
-
−79
Try It 1.6.6
Simplify: −3054
- Answer
-
−59
Sometimes it may not be easy to find common factors of the numerator and denominator. When this happens, a good idea is to factor the numerator and the denominator into prime numbers. Then divide out the common factors using the equivalent fractions property.
Example 1.6.7
Simplify: −210385
Solution



Try It 1.6.8
Simplify: −69120
- Answer
-
−2340
Try It 1.6.9
Simplify: −120192
- Answer
-
−58
We now summarize the steps you should follow to simplify fractions.
SIMPLIFY A FRACTION.
- Rewrite the numerator and denominator to show the common factors.
If needed, factor the numerator and denominator into prime numbers first. - Simplify using the equivalent fractions property by dividing out common factors.
- Multiply any remaining factors, if needed.
Example 1.6.10
Simplify: 5x5y
Solution
| 5x5y | |
| Rewrite showing the common factors, then divide out the common factors. |  |
| Simplify. |
xy |
Try It 1.6.11
Simplify: 7x7y
- Answer
-
xy
Try It 1.6.12
Simplify: 3a3b
- Answer
-
ab
Multiply Fractions
Many people find multiplying and dividing fractions easier than adding and subtracting fractions. So we will start with fraction multiplication.
Doing the Manipulative Mathematics activity “Model Fraction Multiplication” will help you develop a better understanding of multiplying fractions.
We’ll use a model to show you how to multiply two fractions and to help you remember the procedure. Let’s start with 34.

Now we’ll take 12 of 34.

Notice that now, the whole is divided into 8 equal parts. So 12⋅34=38.
To multiply fractions, we multiply the numerators and multiply the denominators.
FRACTION MULTIPLICATION
If a,b,c and d are numbers where b≠0 and d≠0, then
ab⋅cd=acbd
To multiply fractions, multiply the numerators and multiply the denominators.
When multiplying fractions, the properties of positive and negative numbers still apply, of course. It is a good idea to determine the sign of the product as the first step. In Exercise 1.6.13, we will multiply negative and a positive, so the product will be negative.
Example 1.6.13
Multiply: −1112⋅57
Solution
The first step is to find the sign of the product. Since the signs are the different, the product is negative.
−1112⋅57Determine the sign of the product; multiply.−11⋅512⋅7Are there any common factors in the numeratorand the denominator? No−5584
Try It 1.6.14
Multiply: −1028⋅815
- Answer
-
−421
Try It 1.6.15
Multiply: −920⋅512
- Answer
-
−316
When multiplying a fraction by an integer, it may be helpful to write the integer as a fraction. Any integer, a, can be written as a1. So, for example, 3=31.
Example 1.6.16
Multiply: −125(−20x)
Solution
Determine the sign of the product. The signs are the same, so the product is positive.
| −125(−20x) | |
| Write 20x as a fraction. | 125(20x1) |
| Multiply. | |
| Rewrite 20 to show the common factor 5 and divide it out. |  |
| Simplify. | 48x |
Try It 1.6.17
Multiply: 113(−9a)
- Answer
-
−33a
Try It 1.6.18
Multiply: 137(−14b)
- Answer
-
−26b
Divide Fractions
Now that we know how to multiply fractions, we are almost ready to divide. Before we can do that, that we need some vocabulary.
The reciprocal of a fraction is found by inverting the fraction, placing the numerator in the denominator and the denominator in the numerator. The reciprocal of 23 is 32.
Notice that 23⋅32=1. A number and its reciprocal multiply to 1.
To get a product of positive 1 when multiplying two numbers, the numbers must have the same sign. So reciprocals must have the same sign.
The reciprocal of −107 is −710, since −107(−710)=1.
RECIPROCAL
The reciprocal of ab is ba.
A number and its reciprocal multiply to one ab⋅ba=1
Note
Doing the Manipulative Mathematics activity “Model Fraction Division” will help you develop a better understanding of dividing fractions.
To divide fractions, we multiply the first fraction by the reciprocal of the second.
FRACTION DIVISION
If a,b,c and d are numbers where b≠0,c≠0 and d≠0, then
ab÷cd=ab⋅dc
To divide fractions, we multiply the first fraction by the reciprocal of the second.
We need to say b≠0,c≠0 and d≠0 to be sure we don’t divide by zero!
Example 1.6.19
Divide: −23÷n5
Solution
−23÷n5To divide, multiply the first fraction by the−23⋅5nreciprocal of the second.Multiply.−103n
Try It 1.6.20
Divide: −35÷p7.
- Answer
-
−215p
Try It 1.6.21
Divide: −58÷q3.
- Answer
-
−158q
Example 1.6.22
Find the quotient:
−718÷(−1427)
Solution
| −718÷(−1427) | |
| To divide, multiply the first fraction by the reciprocal of the second. | −718⋅−2714 |
| Determine the sign of the product, and then multiply.. | 7⋅2718⋅14 |
| Rewrite showing common factors. |  |
| Remove common factors. | 32⋅2 |
| Simplify. | 34 |
Try It 1.6.23
Find the quotient:
−78÷(−1427)
- Answer
-
415
Try It 1.6.24
Find the quotient:
−78÷(−1427)
- Answer
-
23
There are several ways to remember which steps to take to multiply or divide fractions. One way is to repeat the call outs to yourself. If you do this each time you do an exercise, you will have the steps memorized.
- “To multiply fractions, multiply the numerators and multiply the denominators.”
- “To divide fractions, multiply the first fraction by the reciprocal of the second.”
Another way is to keep two examples in mind:
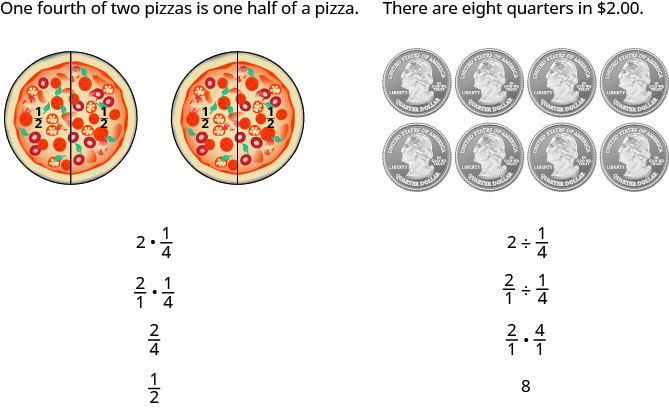
The numerators or denominators of some fractions contain fractions themselves. A fraction in which the numerator or the denominator is a fraction is called a complex fraction.
COMPLEX FRACTION
A complex fraction is a fraction in which the numerator or the denominator contains a fraction.
Some examples of complex fractions are:
6733458x256
To simplify a complex fraction, we remember that the fraction bar means division. For example, the complex fraction 3458 means 34÷58.
Example 1.6.25
Simplify: 3458
Solution
| 3458 | |
| Rewrite as division. | 34÷58 |
| Multiply the first fraction by the reciprocal of the second. | 34⋅85 |
| Multiply. | 3⋅84⋅5 |
| Look for common factors. |  |
| Divide out common factors and simplify. | 65 |
Try It 1.6.26
Simplify: 2356
- Answer
-
45
Try It 1.6.27
Simplify: 37611
- Answer
-
1114
Example 1.6.28
Simplify: x2xy6
Solution
| x2xy6 | |
| Rewrite as division. | x2÷xy6 |
| Multiply the first fraction by the reciprocal of the second. | x2⋅6xy |
| Multiply. | x⋅62⋅xy |
| Look for common factors. | 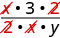 |
| Divide out common factors and simplify. | 3y |
Try It 1.6.29
Simplify: a8ab6
- Answer
-
34b
Try It 1.6.30
Simplify: p2pq8
- Answer
-
4q
Simplify Expressions with a Fraction Bar
The line that separates the numerator from the denominator in a fraction is called a fraction bar. A fraction bar acts as grouping symbol. The order of operations then tells us to simplify the numerator and then the denominator. Then we divide.
To simplify the expression 5−37+1, we first simplify the numerator and the denominator separately. Then we divide.
5−37+12814
SIMPLIFY AN EXPRESSION WITH A FRACTION BAR.
- Simplify the expression in the numerator. Simplify the expression in the denominator.
- Simplify the fraction.
Example 1.6.31
Simplify: 4−2(3)22+2
Solution
4−2(3)22+2Use the order of operations to simplify the4−64+2numerator and the denominator.Simplify the numerator and the denominator−26Simplify. A negative divided by a positive is negative.−13
Try It 1.6.32
Simplify: 6−3(5)32+3
- Answer
-
−34
Try It 1.6.33
Simplify: 4−4(6)32+3
- Answer
-
−53
Where does the negative sign go in a fraction? Usually the negative sign is in front of the fraction, but you will sometimes see a fraction with a negative numerator, or sometimes with a negative denominator. Remember that fractions represent division. When the numerator and denominator have different signs, the quotient is negative.
−13=−13negativepositive=negative1−3=−13positivenegative=negative
PLACEMENT OF NEGATIVE SIGN IN A FRACTION
For any positive numbers a and b,
−ab=a−b=−ab
Example 1.6.34
Simplify: 4(−3)+6(−2)−3(2)−2
Solution
The fraction bar acts like a grouping symbol. So completely simplify the numerator and the denominator separately.
4(−3)+6(−2)−3(2)−2Multiply.−12+(−12)−6−2Simplify.−24−8Divide.3
Try It 1.6.35
Simplify: 8(−2)+4(−3)−5(2)+3
- Answer
-
4
Try It 1.6.36
Simplify: 7(−1)+9(−3)−5(3)−2
- Answer
-
2
Translate Phrases to Expressions with Fractions
Now that we have done some work with fractions, we are ready to translate phrases that would result in expressions with fractions.
The English words quotient and ratio are often used to describe fractions. Remember that “quotient” means division. The quotient of aa and bb is the result we get from dividing a by b, or ab.
Example 1.6.37
Translate the English phrase into an algebraic expression: the quotient of the difference of m and n, and p.
Solution
We are looking for the quotient of the difference of m and n, and p. This means we want to divide the difference of m and n, and p.
m−np
Try It 1.6.38
Translate the English phrase into an algebraic expression: the quotient of the difference of a and b, and cd.
- Answer
-
a−bcd
Try It 1.6.39
Translate the English phrase into an algebraic expression: the quotient of the sum of p and q, and r.
- Answer
-
p+qr
Key Concepts
- Equivalent Fractions Property: If a,b,c are numbers where b≠0,c≠0, then
ab=a⋅cb⋅c and a⋅cb⋅c=ab - Fraction Division: If a,b,c and d are numbers where b≠0,c≠0 and d≠0, then ab÷cd=ab⋅dc. To divide fractions, multiply the first fraction by the reciprocal of the second.
- Fraction Multiplication: If a,b,c and d are numbers where b≠0,d≠0, then ab⋅cd=acbd. To multiply fractions, multiply the numerators and multiply the denominators.
- Placement of Negative Sign in a Fraction: For any positive numbers a and b, −aa=a−a=−ab
- Property of One: aa=1; Any number, except zero, divided by itself is one.
- Simplify a Fraction
- Rewrite the numerator and denominator to show the common factors. If needed, factor the numerator and denominator into prime numbers first.
- Simplify using the equivalent fractions property by dividing out common factors.
- Multiply any remaining factors.
- Simplify an Expression with a Fraction Bar
- Simplify the expression in the numerator. Simplify the expression in the denominator.
- Simplify the fraction.
Glossary
- complex fraction
- A complex fraction is a fraction in which the numerator or the denominator contains a fraction.
- denominator
- The denominator is the value on the bottom part of the fraction that indicates the number of equal parts into which the whole has been divided.
- equivalent fractions
- Equivalent fractions are fractions that have the same value.
- fraction
- A fraction is written ab, where b≠0, a is the numerator and b is the denominator. A fraction represents parts of a whole. The denominator b is the number of equal parts the whole has been divided into, and the numerator aa indicates how many parts are included.
- numerator
- The numerator is the value on the top part of the fraction that indicates how many parts of the whole are included.
- reciprocal
- The reciprocal of ab is ba. A number and its reciprocal multiply to one: ab⋅ba=1.
- simplified fraction
- A fraction is considered simplified if there are no common factors in its numerator and denominator.


