1.8: Decimals
- Last updated
- May 3, 2019
- Save as PDF
- Page ID
- 18927
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Name and write decimals
- Round decimals
- Add and subtract decimals
- Multiply and divide decimals
- Convert decimals, fractions, and percents
Note
A more thorough introduction to the topics covered in this section can be found in the Prealgebrachapter, Decimals.
Name and Write Decimals
Decimals are another way of writing fractions whose denominators are powers of 10.
0.1=1100.1 is "one tenth" 0.01=11000.01 is "one hundredth 0.001=11,0000.001 is "one thousandth 0.0001=110,0000.0001 is "one ten-thousandth"
Notice that “ten thousand” is a number larger than one, but “one ten-thousandth” is a number smaller than one. The “th” at the end of the name tells you that the number is smaller than one.
When we name a whole number, the name corresponds to the place value based on the powers of ten. We read 10,000 as “ten thousand” and 10,000,000 as “ten million.” Likewise, the names of the decimal places correspond to their fraction values. Figure 1.8.1 shows the names of the place values to the left and right of the decimal point.
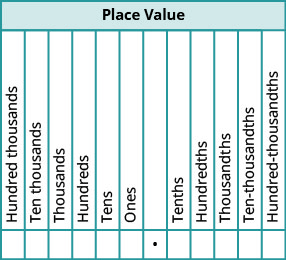
Exercise 1.8.1
Name the decimal 4.3.
- Answer
-




Exercise 1.8.2
Name the decimal 6.7.
- Answer
-
six and seven tenths
Exercise 1.8.3
Name the decimal 5.8.
- Answer
-
five and eight tenths
We summarize the steps needed to name a decimal below.
NAME A DECIMAL.
- Name the number to the left of the decimal point.
- Write “and” for the decimal point.
- Name the “number” part to the right of the decimal point as if it were a whole number.
- Name the decimal place of the last digit.
Exercise 1.8.4
Name the decimal: −15.571.
- Answer
-
−15.571 Name the number to the left of the decimal point. negative fifteen __________________________________ Write “and” for the decimal point. negative fifteen and ______________________________ Name the number to the right of the decimal point. negative fifteen and five hundred seventy-one __________ The 1 is in the thousandths place. negative fifteen and five hundred seventy-one thousandths
Exercise 1.8.5
Name the decimal: −13.461.
- Answer
-
negative thirteen and four hundred sixty-one thousandths
Exercise 1.8.6
Name the decimal: −2.053.
- Answer
-
negative two and fifty-three thousandths
When we write a check we write both the numerals and the name of the number. Let’s see how to write the decimal from the name.
Exercise 1.8.7: How to Write decimals
Write “fourteen and twenty-four thousandths” as a decimal.
- Answer
-




Exercise 1.8.8
Write as a decimal: thirteen and sixty-eight thousandths.
- Answer
-
13.068
Exercise 1.8.9
Write as a decimal: five and ninety-four thousandths.
- Answer
-
5.094
We summarize the steps to writing a decimal.
WRITE A DECIMAL.
- Look for the word “and”—it locates the decimal point.
- Place a decimal point under the word “and.” Translate the words before “and” into the whole number and place it to the left of the decimal point.
- If there is no “and,” write a “0” with a decimal point to its right.
- Mark the number of decimal places needed to the right of the decimal point by noting the place value indicated by the last word.
- Translate the words after “and” into the number to the right of the decimal point. Write the number in the spaces—putting the final digit in the last place.
- Fill in zeros for place holders as needed.
Round Decimals
Rounding decimals is very much like rounding whole numbers. We will round decimals with a method based on the one we used to round whole numbers.
Exercise 1.8.10
Round 18.379 to the nearest hundredth.
- Answer
-




Exercise 1.8.11
Round to the nearest hundredth: 1.047.
- Answer
-
1.05
Exercise 1.8.12
Round to the nearest hundredth: 9.173.
- Answer
-
9.17
We summarize the steps for rounding a decimal here.
ROUND DECIMALS.
- Locate the given place value and mark it with an arrow.
- Underline the digit to the right of the place value.
- Is this digit greater than or equal to 5?
- Yes—add 1 to the digit in the given place value.
- No—do not change the digit in the given place value.
- Rewrite the number, deleting all digits to the right of the rounding digit.
Exercise 1.8.13
Round 18.379 to the nearest
- tenth
- whole number.
- Answer
-
Round 18.379
1. to the nearest tenth
Locate the tenths place with an arrow. 
Underline the digit to the right of the given place value. 
Because 7 is greater than or equal to 5, add 1 to the 3. 
Rewrite the number, deleting all digits to the right of the rounding digit. 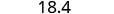
Notice that the deleted digits were NOT replaced with zeros. So, 18.379 rounded to the nearest tenth is 18.4.
2. to the nearest whole numberLocate the ones place with an arrow. 
Underline the digit to the right of the given place value. 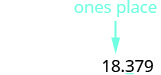
Since 3 is not greater than or equal to 5, do not add 1 to the 8. 
Rewrite the number, deleting all digits to the right of the rounding digit. 
So, 18.379 rounded to the nearest whole number is 18.
Exercise 1.8.14
Round 6.582 to the nearest
- hundredth
- tenth
- whole number.
- Answer
-
- 6.58
- 6.6
- 7
Exercise 1.8.15
Round 15.2175 to the nearest
- thousandth
- hundredth
- tenth.
- Answer
-
- 15.218
- 15.22
- 15.2
Add and Subtract Decimals
To add or subtract decimals, we line up the decimal points. By lining up the decimal points this way, we can add or subtract the corresponding place values. We then add or subtract the numbers as if they were whole numbers and then place the decimal point in the sum.
ADD OR SUBTRACT DECIMALS.
- Write the numbers so the decimal points line up vertically.
- Use zeros as place holders, as needed.
- Add or subtract the numbers as if they were whole numbers. Then place the decimal point in the answer under the decimal points in the given numbers.
Exercise 1.8.16
Add: 23.5+41.38.
- Answer
-
Write the numbers so that the decimal points line up vertically.23.50+41.38
Put 0 as a placeholder after the 5 in 23.5. Remember, 510=50100, so 0.5=0.5023.50+41.38
Add the numbers as if they were whole numbers . Then place the decimal point in the sum.23.50+41.3864.88
Exercise 1.8.17
Add: 4.8+11.69.
- Answer
-
16.49
Exercise 1.8.18
Add: 5.123+18.47.
- Answer
-
23.593
Exercise 1.8.19
Subtract: 20−14.65.
- Answer
-
Write the numbers so that the decimal points line up vertically.20−14.6520.−14.65Remember, 20 is a whole number, so place the decimal point after the 0.
Put zeros to the right as placeholders.20.00−14.65
Write the numbers so that the decimal points line up vertically.991⧸10⧸10⧸10⧸2⧸0.⧸0⧸0−14.655.35
Exercise 1.8.20
Subtract: 10−9.58.
- Answer
-
0.42
Exercise 1.8.21
Subtract: 50−37.42.
- Answer
-
12.58
Multiply and Divide Decimals
Multiplying decimals is very much like multiplying whole numbers—we just have to determine where to place the decimal point. The procedure for multiplying decimals will make sense if we first convert them to fractions and then multiply.
So let’s see what we would get as the product of decimals by converting them to fractions first. We will do two examples side-by-side. Look for a pattern!
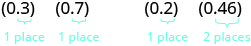 |
|
Convert to fractions. |
 |
| Multiply. |  |
| Convert to decimals. |  |
Notice, in the first example, we multiplied two numbers that each had one digit after the decimal point and the product had two decimal places. In the second example, we multiplied a number with one decimal place by a number with two decimal places and the product had three decimal places.
We multiply the numbers just as we do whole numbers, temporarily ignoring the decimal point. We then count the number of decimal points in the factors and that sum tells us the number of decimal places in the product.
The rules for multiplying positive and negative numbers apply to decimals, too, of course!
When multiplying two numbers,
- if their signs are the same the product is positive.
- if their signs are different the product is negative.
When we multiply signed decimals, first we determine the sign of the product and then multiply as if the numbers were both positive. Finally, we write the product with the appropriate sign.
MULTIPLY DECIMALS.
- Determine the sign of the product.
- Write in vertical format, lining up the numbers on the right. Multiply the numbers as if they were whole numbers, temporarily ignoring the decimal points.
- Place the decimal point. The number of decimal places in the product is the sum of the number of decimal places in the factors.
- Write the product with the appropriate sign.
Exercise 1.8.22
Multiply: (−3.9)(4.075).
- Answer
-
(−3.9)(4.075) The signs are different. The product will be negative. Write in vertical format, lining up the numbers on the right. 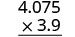
Multiply. 
Add the number of decimal places in the factors (1+3).

Place the decimal point 4 places from the right.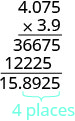
The signs are different, so the product is negative. (−3.9)(4.075)=−15.8925
Exercise 1.8.23
Multiply: −4.5(6.107).
- Answer
-
−27.4815
Exercise 1.8.24
Multiply: −10.79(8.12).
- Answer
-
−87.6148
In many of your other classes, especially in the sciences, you will multiply decimals by powers of 10 (10, 100, 1000, etc.). If you multiply a few products on paper, you may notice a pattern relating the number of zeros in the power of 10 to number of decimal places we move the decimal point to the right to get the product.
MULTIPLY A DECIMAL BY A POWER OF TEN.
- Move the decimal point to the right the same number of places as the number of zeros in the power of 10.
- Add zeros at the end of the number as needed.
Exercise 1.8.25
Multiply 5.63
- by 10
- by 100
- by 1,000.
- Answer
-
By looking at the number of zeros in the multiple of ten, we see the number of places we need to move the decimal to the right.
ⓐ
5.63(10) There is 1 zero in 10, so move the decimal point 1 place to the right. 
ⓑ
5.63(100) There are 2 zeros in 100, so move the decimal point 2 places to the right. 
ⓒ
There are 3 zeros in 1,000, so move the decimal point 3 places to the right. 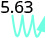
A zero must be added at the end. 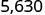
Exercise 1.8.26
Multiply 2.58
- by 10
- by 100
- by 1,000.
- Answer
-
- 25.8
- 258
- 2,580
Exercise 1.8.27
Multiply 14.2
- by 10
- by 100
- by 1,000.
- Answer
-
- 142
- 1,420
- 14,200
Just as with multiplication, division of decimals is very much like dividing whole numbers. We just have to figure out where the decimal point must be placed.
To divide decimals, determine what power of 10 to multiply the denominator by to make it a whole number. Then multiply the numerator by that same power of 10. Because of the equivalent fractions property, we haven’t changed the value of the fraction! The effect is to move the decimal points in the numerator and denominator the same number of places to the right. For example:
0.80.40.8(10)0.4(10)84
We use the rules for dividing positive and negative numbers with decimals, too. When dividing signed decimals, first determine the sign of the quotient and then divide as if the numbers were both positive. Finally, write the quotient with the appropriate sign.
We review the notation and vocabulary for division:
cquotientadividend÷bdivisor=cquotientbdivisor)¯adividend
We’ll write the steps to take when dividing decimals, for easy reference.
DIVIDE DECIMALS.
- Determine the sign of the quotient.
- Make the divisor a whole number by “moving” the decimal point all the way to the right. “Move” the decimal point in the dividend the same number of places—adding zeros as needed.
- Divide. Place the decimal point in the quotient above the decimal point in the dividend.
- Write the quotient with the appropriate sign.
Exercise 1.8.28
Divide: −25.65÷(−0.06).
- Answer
-
Remember, you can “move” the decimals in the divisor and dividend because of the Equivalent Fractions Property.
−25.65÷(−0.06) The signs are the same. The quotient is positive. Make the divisor a whole number by “moving” the decimal point all the way to the right. “Move” the decimal point in the dividend the same number of places. 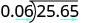
Divide.
Place the decimal point in the quotient above the decimal point in the dividend.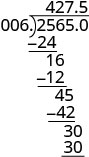
Write the quotient with the appropriate sign. −25.65÷(−0.06)=427.5
Exercise 1.8.29
Divide: −23.492÷(−0.04).
- Answer
-
687.3
Exercise 1.8.30
Divide: −4.11÷(−0.12).
- Answer
-
34.25
A common application of dividing whole numbers into decimals is when we want to find the price of one item that is sold as part of a multi-pack. For example, suppose a case of 24 water bottles costs $3.99. To find the price of one water bottle, we would divide $3.99 by 24. We show this division in Exercise 1.8.31. In calculations with money, we will round the answer to the nearest cent (hundredth).
Exercise 1.8.31
Divide: $3.99÷24.
- Answer
-
.99 divided by 24 is given. A long division problem is set up with 24 dividing 3.99. A table is given with directions on the left and the mathematical steps on the right. The first step reads “Place the decimal point in the quotient above the decimal point in the dividend. Divide as usual. When do we stop? Since this division involves money, we round it to the nearest cent (hundredth). To do this, we must carry the division to the thousandths place.” To the right of this, we have a long division problem set up with 24 dividing 3.990. The quotient is given as 0.166. To show the work, below 3.990 it reads 24, solid horizontal line, 159, 144, solid horizontal line, 150, 144, solid horizontal line, and finally 6. The fifth step reads “Round to the nearest cent.” To the right of this, we have $0.166 is approximately equal to $0.17 and hence >.99 divided by 24 is $0.17.">
$3.99÷24 Place the decimal point in the quotient above the decimal point in the dividend. Divide as usual.
When do we stop? Since this division involves money, we round it to the nearest cent (hundredth.) To do this, we must carry the division to the thousandths place.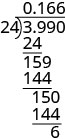
Round to the nearest cent. $0.166≈$0.17
$3.99÷2≈$0.17
Exercise 1.8.32
Divide: $6.99÷36.
- Answer
-
$0.19
Exercise 1.8.33
Divide: $4.99÷12.
- Answer
-
$0.42
Convert Decimals, Fractions, and Percents
We convert decimals into fractions by identifying the place value of the last (farthest right) digit. In the decimal 0.03 the 3 is in the hundredths place, so 100 is the denominator of the fraction equivalent to 0.03.
00.03=3100
Notice, when the number to the left of the decimal is zero, we get a fraction whose numerator is less than its denominator. Fractions like this are called proper fractions.
The steps to take to convert a decimal to a fraction are summarized in the procedure box.
CONVERT A DECIMAL TO A PROPER FRACTION.
- Determine the place value of the final digit.
- Write the fraction.
- numerator—the “numbers” to the right of the decimal point
- denominator—the place value corresponding to the final digit
Exercise 1.8.34
Write 0.374 as a fraction.
- Answer
-
0.374 Determine the place value of the final digit. 
Write the fraction for 0.374:
- The numerator is 374.
- The denominator is 1,000.
3741000 Simplify the fraction. 2⋅1872⋅500 Divide out the common factors. 187500
so, 0.374=187500Did you notice that the number of zeros in the denominator of 3741000 is the same as the number of decimal places in 0.374?
Exercise 1.8.35
Write 0.234 as a fraction.
- Answer
-
117500
Exercise 1.8.36
Write 0.024 as a fraction.
- Answer
-
3125
We’ve learned to convert decimals to fractions. Now we will do the reverse—convert fractions to decimals. Remember that the fraction bar means division. So 45 can be written 4÷5 or 5)¯4. This leads to the following method for converting a fraction to a decimal.
CONVERT A FRACTION TO A DECIMAL.
To convert a fraction to a decimal, divide the numerator of the fraction by the denominator of the fraction.
Exercise 1.8.37
Write −58 as a decimal.
- Answer
-
Since a fraction bar means division, we begin by writing 58 as 8)¯5. Now divide.

Exercise 1.8.38
Write −78 as a decimal.
- Answer
-
−0.875
Exercise 1.8.39
Write −38 as a decimal.
- Answer
-
−0.375
When we divide, we will not always get a zero remainder. Sometimes the quotient ends up with a decimal that repeats. A repeating decimal is a decimal in which the last digit or group of digits repeats endlessly. A bar is placed over the repeating block of digits to indicate it repeats.
REPEATING DECIMAL
A repeating decimal is a decimal in which the last digit or group of digits repeats endlessly.
A bar is placed over the repeating block of digits to indicate it repeats.
Exercise 1.8.40
Write 4322 as a decimal.
- Answer
-
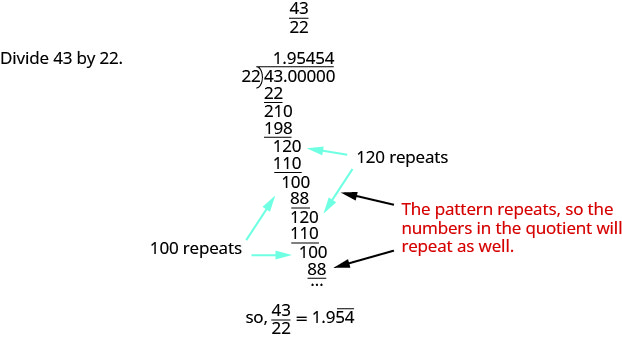
Exercise 1.8.41
Write 2711 as a decimal.
- Answer
-
2.¯45
Exercise 1.8.42
Write 5122 as a decimal.
- Answer
-
2.3¯18
Sometimes we may have to simplify expressions with fractions and decimals together.
Exercise 1.8.43
Simplify: 78+6.4.
- Answer
-
First we must change one number so both numbers are in the same form. We can change the fraction to a decimal, or change the decimal to a fraction. Usually it is easier to change the fraction to a decimal.
78+6.4 Change 78 to a decimal. 
Add. 0.875+6.4 7.275 So, 78+6.4=7.275
Exercise 1.8.44
Simplify: 38+4.9.
- Answer
-
5.275
Exercise 1.8.45
Simplify: 5.7+1320.
- Answer
-
6.35
A percent is a ratio whose denominator is 100. Percent means per hundred. We use the percent symbol, %, to show percent.
PERCENT
A percent is a ratio whose denominator is 100.
Since a percent is a ratio, it can easily be expressed as a fraction. Percent means per 100, so the denominator of the fraction is 100. We then change the fraction to a decimal by dividing the numerator by the denominator.
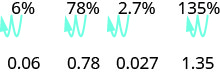
6%78%135% Write as a ratio with denominator 100.610078100135100 Change the fraction to a decimal by dividing0.060.781.35the numerator by the denominator.
Do you see the pattern? To convert a percent number to a decimal number, we move the decimal point two places to the left.
Exercise 1.8.46
Convert each percent to a decimal:
- 62%
- 135%
- 35.7%.
- Answer
-
1. 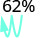
Move the decimal point two places to the left. 0.62 2. 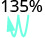
Move the decimal point two places to the left. 1.35 3. 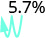
Move the decimal point two places to the left. 0.057
Exercise 1.8.47
Convert each percent to a decimal:
- 9%
- 87%
- 3.9%.
- Answer
-
- 0.09
- 0.87
- 0.039
Exercise 1.8.48
Convert each percent to a decimal:
- 3%
- 91%
- 8.3%.
- Answer
-
- 0.03
- 0.91
- 0.083
Converting a decimal to a percent makes sense if we remember the definition of percent and keep place value in mind.
To convert a decimal to a percent, remember that percent means per hundred. If we change the decimal to a fraction whose denominator is 100, it is easy to change that fraction to a percent.
0.831.050.075Write as a fraction 8310015100751000The denominator is 100.1051007.5100Write the ratio as a percent.83%105%7.5%
Recognize the pattern? To convert a decimal to a percent, we move the decimal point two places to the right and then add the percent sign.
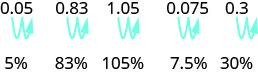
Exercise 1.8.49
Convert each decimal to a percent:
- 0.51
- 1.25
- 0.093.
- Answer
-
1. 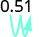
Move the decimal point two places to the right. 51 2. 
Move the decimal point two places to the right. 125 3. 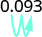
Move the decimal point two places to the right. 9.3
Exercise 1.8.50
Convert each decimal to a percent:
- 0.17
- 1.75
- 0.0825
- Answer
-
- 17%
- 175%
- 8.25%
Exercise 1.8.51
Convert each decimal to a percent:
- 0.41
- 2.25
- 0.0925.
- Answer
-
- 41%
- 225%
- 9.25%
Key Concepts
- Name a Decimal
- Name the number to the left of the decimal point.
- Write ”and” for the decimal point.
- Name the “number” part to the right of the decimal point as if it were a whole number.
- Name the decimal place of the last digit.
- Write a Decimal
- Look for the word ‘and’—it locates the decimal point. Place a decimal point under the word ‘and.’ Translate the words before ‘and’ into the whole number and place it to the left of the decimal point. If there is no “and,” write a “0” with a decimal point to its right.
- Mark the number of decimal places needed to the right of the decimal point by noting the place value indicated by the last word.
- Translate the words after ‘and’ into the number to the right of the decimal point. Write the number in the spaces—putting the final digit in the last place.
- Fill in zeros for place holders as needed.
- Round a Decimal
- Locate the given place value and mark it with an arrow.
- Underline the digit to the right of the place value.
- Is this digit greater than or equal to 5? Yes—add 1 to the digit in the given place value. No—do not change the digit in the given place value.
- Rewrite the number, deleting all digits to the right of the rounding digit.
- Add or Subtract Decimals
- Write the numbers so the decimal points line up vertically.
- Use zeros as place holders, as needed.
- Add or subtract the numbers as if they were whole numbers. Then place the decimal in the answer under the decimal points in the given numbers.
- Multiply Decimals
- Determine the sign of the product.
- Write in vertical format, lining up the numbers on the right. Multiply the numbers as if they were whole numbers, temporarily ignoring the decimal points.
- Place the decimal point. The number of decimal places in the product is the sum of the decimal places in the factors.
- Write the product with the appropriate sign.
- Multiply a Decimal by a Power of Ten
- Move the decimal point to the right the same number of places as the number of zeros in the power of 10.
- Add zeros at the end of the number as needed.
- Divide Decimals
- Determine the sign of the quotient.
- Make the divisor a whole number by “moving” the decimal point all the way to the right. “Move” the decimal point in the dividend the same number of places - adding zeros as needed.
- Divide. Place the decimal point in the quotient above the decimal point in the dividend.
- Write the quotient with the appropriate sign.
- Convert a Decimal to a Proper Fraction
- Determine the place value of the final digit.
- Write the fraction: numerator—the ‘numbers’ to the right of the decimal point; denominator—the place value corresponding to the final digit.
- Convert a Fraction to a Decimal Divide the numerator of the fraction by the denominator.


