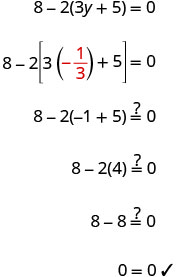2.4: Use a General Strategy to Solve Linear Equations
- Page ID
- 18935
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Solve equations using a general strategy
- Classify equations
Note
Before you get started, take this readiness quiz.
- Simplify: −(a−4).
If you missed this problem, review Exercise 1.10.46 - Multiply: 32(12x+20)
If you missed this problem, review Exercise 1.10.34. - Simplify: 5−2(n+1)
If you missed this problem, review Exercise 1.10.49. - Multiply: 3(7y+9)
If you missed this problem, review Exercise 1.10.34. - Multiply: (2.5)(6.4)
If you missed this problem, review Exercise 1.8.19.
Solve Equations Using the General Strategy
Until now we have dealt with solving one specific form of a linear equation. It is time now to lay out one overall strategy that can be used to solve any linear equation. Some equations we solve will not require all these steps to solve, but many will.
Beginning by simplifying each side of the equation makes the remaining steps easier.
Example 2.4.1: How to Solve Linear Equations Using the General Strategy
Solve: −6(x+3)=24.
Solution





Try It 2.4.2
Solve: 5(x+3)=35
- Answer
-
x=4
Try It 2.4.3
Solve: 6(y−4)=−18
- Answer
-
y=1
GENERAL STRATEGY FOR SOLVING LINEAR EQUATIONS.
- Simplify each side of the equation as much as possible.
Use the Distributive Property to remove any parentheses.
Combine like terms. - Collect all the variable terms on one side of the equation.
Use the Addition or Subtraction Property of Equality. - Collect all the constant terms on the other side of the equation.
Use the Addition or Subtraction Property of Equality. - Make the coefficient of the variable term to equal to 1.
Use the Multiplication or Division Property of Equality.
State the solution to the equation. - Check the solution. Substitute the solution into the original equation to make sure the result is a true statement.
Example 2.4.4
Solve: −(y+9)=8
Solution
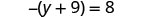 |
||
| Simplify each side of the equation as much as possible by distributing. | 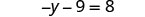 |
|
| The only y term is on the left side, so all variable terms are on the left side of the equation. | ||
| Add 9 to both sides to get all constant terms on the right side of the equation. |  |
|
| Simplify. | 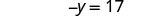 |
|
| Rewrite −y as −1y. | 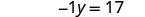 |
|
| Make the coefficient of the variable term to equal to 1 by dividing both sides by −1. | 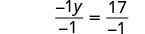 |
|
| Simplify. |  |
|
| Check: | 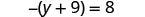 |
|
| Let y=−17. | 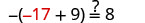 |
|
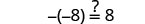 |
||
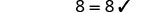 |
||
Try It 2.4.5
Solve: −(y+8)=−2
- Answer
-
y=−6
Try It 2.4.6
Solve: −(z+4)=−12
- Answer
-
z=8
Example 2.4.7
Solve: 5(a−3)+5=−10
Solution
 |
||
| Simplify each side of the equation as much as possible. | ||
| Distribute. |  |
|
| Combine like terms. | 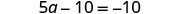 |
|
| The only a term is on the left side, so all variable terms are on one side of the equation. | ||
| Add 10 to both sides to get all constant terms on the other side of the equation. |  |
|
| Simplify. | 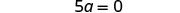 |
|
| Make the coefficient of the variable term to equal to 11 by dividing both sides by 55. | 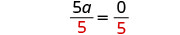 |
|
| Simplify. | 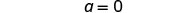 |
|
| Check: | 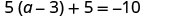 |
|
| Let a=0. | 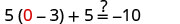 |
|
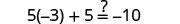 |
||
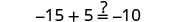 |
||
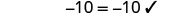 |
||
Try It 2.4.8
Solve: 2(m−4)+3=−1
- Answer
-
m=2
Try It 2.4.9
Solve:7(n−3)−8=−15
- Answer
-
n=2
Example 2.4.10
Solve: 23(6m−3)=8−m
Solution
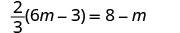 |
||
| Distribute. | 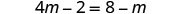 |
|
| Add m to get the variables only to the left. | 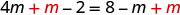 |
|
| Simplify. | 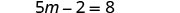 |
|
| Add 2 to get constants only on the right. | 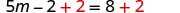 |
|
| Simplify. | 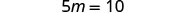 |
|
| Divide by 5. | 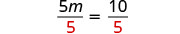 |
|
| Simplify. | 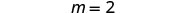 |
|
| Check: | 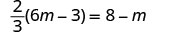 |
|
| Let m=2. | 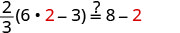 |
|
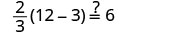 |
||
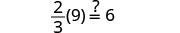 |
||
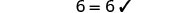 |
||
Try It 2.4.11
Solve: 13(6u+3)=7−u
- Answer
-
u=2
Try It 2.4.12
Solve: 23(9x−12)=8+2x
- Answer
-
x=4
Example 2.4.13
Solve: 8−2(3y+5)=0
Solution
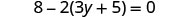 |
|
| Simplify—use the Distributive Property. | 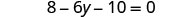 |
| Combine like terms. | 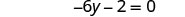 |
| Add 2 to both sides to collect constants on the right. | 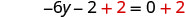 |
| Simplify. | 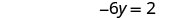 |
| Divide both sides by −6−6. | 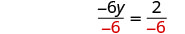 |
| Simplify. |  |
|
Check: Let y=−13.
|
Try It 2.4.14
Solve: 12−3(4j+3)=−17
- Answer
-
j=53
Try It 2.4.15
Solve: −6−8(k−2)=−10
- Answer
-
k=52
Example 2.4.16
Solve: 4(x−1)−2=5(2x+3)+6
Solution
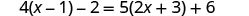 |
||
| Distribute. | 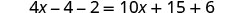 |
|
| Combine like terms. | 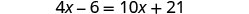 |
|
| Subtract 4x to get the variables only on the right side since 10>4. |  |
|
| Simplify. | 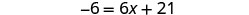 |
|
| Subtract 21 to get the constants on left. | 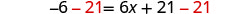 |
|
| Simplify. | 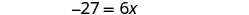 |
|
| Divide by 6. | 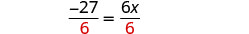 |
|
| Simplify. | 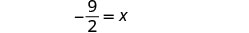 |
|
| Check: |  |
|
| Let x=−92. | 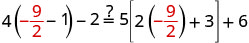 |
|
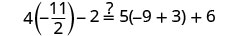 |
||
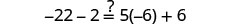 |
||
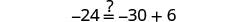 |
||
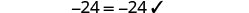 |
||
Try It 2.4.17
Solve: 6(p−3)−7=5(4p+3)−12
- Answer
-
p=−2
Try It 2.4.18
Solve: 8(q+1)−5=3(2q−4)−1
- Answer
-
q=−8
Example 2.4.19
Solve: 10[3−8(2s−5)]=15(40−5s)
Solution
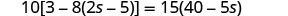 |
||
| Simplify from the innermost parentheses first. | 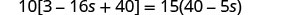 |
|
| Combine like terms in the brackets. | 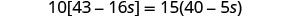 |
|
| Distribute. | 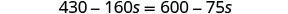 |
|
| Add 160s to get the s’s to the right. | 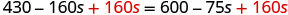 |
|
| Simplify. | 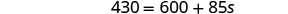 |
|
| Subtract 600 to get the constants to the left. | 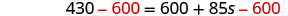 |
|
| Simplify. | 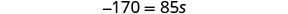 |
|
| Divide. | 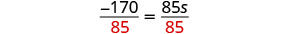 |
|
| Simplify. | 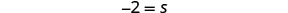 |
|
| Check: | 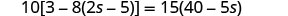 |
|
| Substitute s=−2. | 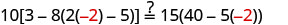 |
|
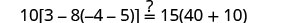 |
||
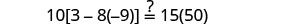 |
||
 |
||
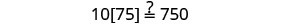 |
||
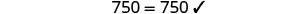 |
||
Try It 2.4.20
Solve: 6[4−2(7y−1)]=8(13−8y).
- Answer
-
y=−175
Try It 2.4.21
Solve: 12[1−5(4z−1)]=3(24+11z).
- Answer
-
z=0
Example 2.4.22
Solve: 0.36(100n+5)=0.6(30n+15).
Solution
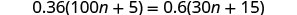 |
||
| Distribute. | 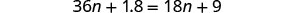 |
|
| Subtract 18n to get the variables to the left. | 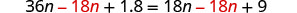 |
|
| Simplify. | 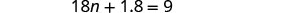 |
|
| Subtract 1.8 to get the constants to the right. | 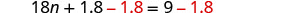 |
|
| Simplify. | 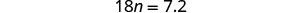 |
|
| Divide. | 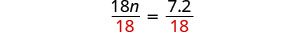 |
|
| Simplify. | 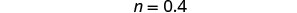 |
|
| Check: | 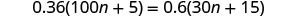 |
|
| Let n=0.4. | 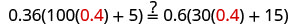 |
|
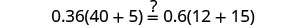 |
||
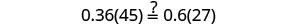 |
||
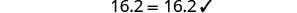 |
||
Try It 2.4.23
Solve: 0.55(100n+8)=0.6(85n+14).
- Answer
-
n=1
Try It 2.4.24
Solve: 0.15(40m−120)=0.5(60m+12).
- Answer
-
m=−1
Classify Equations
Consider the equation we solved at the start of the last section, 7x+8=−13. The solution we found was x=−3. This means the equation 7x+8=−13 is true when we replace the variable, x, with the value −3. We showed this when we checked the solution x=−3 and evaluated 7x+8=−13 for x=−3.
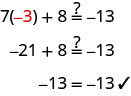
If we evaluate 7x+8 for a different value of x, the left side will not be −13.
The equation 7x+8=−13 is true when we replace the variable, x, with the value −3, but not true when we replace x with any other value. Whether or not the equation 7x+8=−13 is true depends on the value of the variable. Equations like this are called conditional equations.
All the equations we have solved so far are conditional equations.
CONDITIONAL EQUATION
An equation that is true for one or more values of the variable and false for all other values of the variable is a conditional equation.
Now let’s consider the equation 2y+6=2(y+3). Do you recognize that the left side and the right side are equivalent? Let’s see what happens when we solve for y.
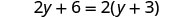 |
|
| Distribute. | 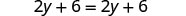 |
| Subtract 2y to get the y’s to one side. | 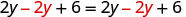 |
| Simplify—the y’s are gone! | 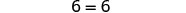 |
But 6=6 is true.
This means that the equation 2y+6=2(y+3) is true for any value of y. We say the solution to the equation is all of the real numbers. An equation that is true for any value of the variable like this is called an identity.
IDENTITY
An equation that is true for any value of the variable is called an identity.
The solution of an identity is all real numbers.
What happens when we solve the equation 5z=5z−1?
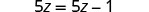 |
|
| Subtract 5z to get the constant alone on the right. | 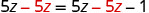 |
| Simplify—the z’s are gone! | 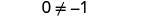 |
But 0≠−1.
Solving the equation 5z=5z−1 led to the false statement 0=−1. The equation 5z=5z−1 will not be true for any value of z. It has no solution. An equation that has no solution, or that is false for all values of the variable, is called a contradiction.
CONTRADICTION
An equation that is false for all values of the variable is called a contradiction.
A contradiction has no solution.
Example 2.4.25
Classify the equation as a conditional equation, an identity, or a contradiction. Then state the solution.
6(2n−1)+3=2n−8+5(2n+1)
Solution
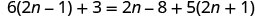 |
|
| Distribute. | 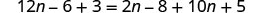 |
| Combine like terms. | 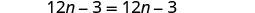 |
| Subtract 12n to get the nn’s to one side. | 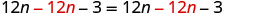 |
| Simplify. | 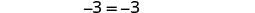 |
| This is a true statement. | The equation is an identity. The solution is all real numbers. |
Try It 2.4.26
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution:
4+9(3x−7)=−42x−13+23(3x−2)
Answer-
identity; all real numbers
Try It 2.4.27
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution:
8(1−3x)+15(2x+7)=2(x+50)+4(x+3)+1
Answer-
identity; all real numbers
Example 2.4.28
Classify as a conditional equation, an identity, or a contradiction. Then state the solution.
10+4(p−5)=0
Solution
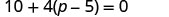 |
|
| Distribute. | 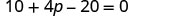 |
| Combine like terms. | 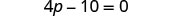 |
| Add 10 to both sides. |  |
| Simplify. | 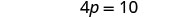 |
| Divide. | 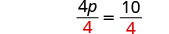 |
| Simplify. | 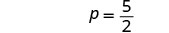 |
| The equation is true when p=frac52. | This is a conditional equation. The solution is p=frac52. |
Try It 2.4.29
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution: 11(q+3)−5=19
- Answer
-
conditional equation; \(q = \frac{9}{11}\
Try It 2.4.30
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution: 6+14(k−8)=95
- Answer
-
conditional equation; k=19314
Example 2.4.31
Classify the equation as a conditional equation, an identity, or a contradiction. Then state the solution.
5m+3(9+3m)=2(7m−11)
Solution
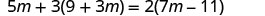 |
|
| Distribute. | 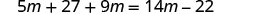 |
| Combine like terms. | 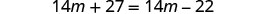 |
| Subtract 14m from both sides. | 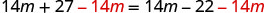 |
| Simplify. | 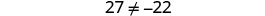 |
| But 27≠−22. | The equation is a contradiction. It has no solution. |
Try It 2.4.32
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution:
12c+5(5+3c)=3(9c−4)
Answer-
contradiction; no solution
Try It 2.4.33
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution:
4(7d+18)=13(3d−2)−11d
Answer-
contradiction; no solution
| Type of equation | What happens when you solve it? | Solution |
|---|---|---|
| Conditional Equation | True for one or more values of the variables and false for all other values | One or more values |
| Identity | True for any value of the variable | All real numbers |
| Contradiction | False for all values of the variable | No solution |
Key Concepts
- General Strategy for Solving Linear Equations
- Simplify each side of the equation as much as possible.
Use the Distributive Property to remove any parentheses.
Combine like terms. - Collect all the variable terms on one side of the equation.
Use the Addition or Subtraction Property of Equality. - Collect all the constant terms on the other side of the equation.
Use the Addition or Subtraction Property of Equality. - Make the coefficient of the variable term to equal to 1.
Use the Multiplication or Division Property of Equality.
State the solution to the equation. - Check the solution.
Substitute the solution into the original equation.
- Simplify each side of the equation as much as possible.