Skip to main content
Mathematics LibreTexts

8.5: Simplify Complex Rational Expressions

  1. Last updated
  2. Save as PDF
  • Page ID
    18981

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Learning Objectives

    By the end of this section, you will be able to:

    • Simplify a complex rational expression by writing it as division
    • Simplify a complex rational expression by using the LCD
    Note

    Before you get started, take this readiness quiz.

    If you miss a problem, go back to the section listed and review the material.

    1. Simplify: \(\frac{\frac{3}{5}}{\frac{9}{10}}\).
      If you missed this problem, review Exercise 1.6.25.
    2. Simplify: \(\frac{1−\frac{1}{3}}{4^2+4·5}\).
      If you missed this problem, review Exercise 1.6.31.

    Complex fractions are fractions in which the numerator or denominator contains a fraction. In Chapter 1 we simplified complex fractions like these:

    \[\begin{array}{cc} {\frac{\frac{3}{4}}{\frac{5}{8}}}&{\frac{\frac{x}{2}}{\frac{xy}{6}}}\\ \nonumber \end{array}\]

    In this section we will simplify complex rational expressions, which are rational expressions with rational expressions in the numerator or denominator.

    Definition: COMPLEX RATIONAL EXPRESSION

    A complex rational expression is a rational expression in which the numerator or denominator contains a rational expression.

    Here are a few complex rational expressions:

    \(\frac{\frac{4}{y−3}}{\frac{8}{y^2−9}}\)

    \(\frac{\frac{1}{x}+\frac{1}{y}}{\frac{x}{y}−\frac{y}{x}}\)

    \(\frac{\frac{2}{x+6}}{\frac{4}{x−6}−\frac{4}{x^2−36}}\)
    Remember, we always exclude values that would make any denominator zero.

    We will use two methods to simplify complex rational expressions.

    Simplify a Complex Rational Expression by Writing it as Division

    We have already seen this complex rational expression earlier in this chapter.

    \(\frac{\frac{6x^2−7x+2}{4x−8}}{\frac{2x^2−8x+3}{x^2−5x+6}}\)

    We noted that fraction bars tell us to divide, so rewrote it as the division problem

    \((\frac{6x^2−7x+2}{4x−8})÷(\frac{2x^2−8x+3}{x^2−5x+6})\)

    Then we multiplied the first rational expression by the reciprocal of the second, just like we do when we divide two fractions.

    This is one method to simplify rational expressions. We write it as if we were dividing two fractions.

    Example \(\PageIndex{1}\)

    \(\frac{\frac{4}{y−3}}{\frac{8}{y^2−9}}\).

    Answer
      \(\frac{\frac{4}{y−3}}{\frac{8}{y^2−9}}\)
    Rewrite the complex fraction as division. \(\frac{4}{y−3}÷\frac{8}{y^2−9}\)
    Rewrite as the product of first times the reciprocal of the second. \(\frac{4}{y−3}·\frac{y^2−9}{8}\)
    Multiply. \(\frac{4(y^2−9)}{8(y−3)}\)
    Factor to look for common factors. \(\frac{4(y−3)(y+3)}{8(y−3)}\)
    Simplify. \(\frac{y+3}{2}\)

    Are there any value(s) of y that should not be allowed? The simplified rational expression has just a constant in the denominator. But the original complex rational expression had denominators of y−3 and \(y^2−9\). This expression would be undefined if y=3 or y=−3

    Example \(\PageIndex{2}\)

    \(\frac{\frac{2}{x^2−1}}{\frac{3}{x+1}}\).

    Answer

    \(\frac{2}{3(x−1)}\)

    Example \(\PageIndex{3}\)

    \(\frac{\frac{1}{x^2−7x+12}}{\frac{2}{x−4}}\).

    Answer

    \(\frac{1}{2(x−3)}\)

    Example \(\PageIndex{4}\)

    \(\frac{\frac{1}{3}+\frac{1}{6}}{\frac{1}{2}−\frac{1}{3}}\).

    Answer
      .
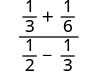
    Simplify the numerator and denominator.  
    Find the LCD and add the fractions in the numerator.
    Find the LCD and add the fractions in the denominator.    		 .
    Simplify the numerator and denominator. .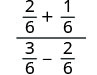
    Simplify the numerator and denominator, again. .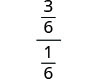
    Rewrite the complex rational expression as a division problem. .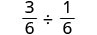
    Multiply the first times by the reciprocal of the second. .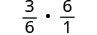
    Simplify. .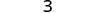
    Example \(\PageIndex{5}\)

    \(\frac{\frac{1}{2}+\frac{2}{3}}{\frac{5}{6}+\frac{1}{12}}\).

    Answer

    \(\frac{14}{11}\)

    Example \(\PageIndex{6}\)

    \(\frac{\frac{3}{4}−\frac{1}{3}}{\frac{1}{8}+\frac{5}{6}}\).

    Answer

    \(\frac{10}{23}\)

    How to Simplify a Complex Rational Expression by Writing it as Division

    Example \(\PageIndex{7}\)

    \(\frac{\frac{1}{x}+\frac{1}{y}}{\frac{x}{y}−\frac{y}{x}}\).

    Answer

    The above image has three columns. The image shows steps on how to divide complex rational expressions in three steps. Step one is to simplify the numerator and denominator. We will simplify the sum in the numerator and difference in the denominator for the example 1 divided by x plus 1 divided by y divided by x divided by y minus y divided by x. Find a common denominator and add the fractions in the numerator and find a common denominator and subtract the fractions in the numerator to get 1 times y divided by x times y plus 1 times x divided by y times x divided by x times x divided by y times x minus y times y divided by x times y. Then, we get y divided by x y plus x plus x y divided by x squared divided by x y minus y squared divided by x y. We now have just one rational expression in the numerator and one in the denominator, y plus x divided by x y divided by x squared minus y squared divided by x y.Step two is to rewrite the complex rational expression as a division problem. We write the numerator divided by the denominator.Step three is to divide the expressions. Multiply the first by the reciprocal of the second to get y plus x divided by x y times x y divided by x squared minus y squared. Factor any expressions if possible. We now have x y times y plus x divided by x y times x minus y times x plus y. Remove common factors. Cross out x, y and y plus x from the numerator. Cross out x, y and x plus y from the denominator. Simplify to get 1 divided by x minus y.

    Example \(\PageIndex{8}\)

    \(\frac{\frac{1}{x}+\frac{1}{y}}{\frac{1}{x}−\frac{1}{y}}\).

    Answer

    \(\frac{y+x}{y−x}\)

    Example \(\PageIndex{9}\)

    \(\frac{\frac{1}{a}+\frac{1}{b}}{\frac{1}{a^2}−\frac{1}{b^2}}\).

    Answer

    \(\frac{ab}{b−a}\)

    Definition: SIMPLIFY A COMPLEX RATIONAL EXPRESSION BY WRITING IT AS DIVISION.
    1. Simplify the numerator and denominator.
    2. Rewrite the complex rational expression as a division problem.
    3. Divide the expressions.
    Example \(\PageIndex{10}\)

    \(\frac{n−\frac{4n}{n+5}}{\frac{1}{n+5}+\frac{1}{n−5}}\)

    Answer
      .
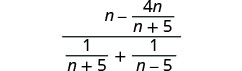
    Simplify the numerator and denominator.  
    Find the LCD and add the fractions in the numerator.
    Find the LCD and add the fractions in the denominator.    		 .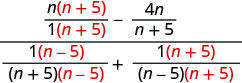
    Simplify the numerators. .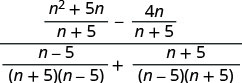

    Subtract the rational expressions in the numerator and add in the denominator.    		 .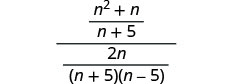
    Rewrite as fraction division. .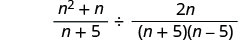
    Multiply the first times the reciprocal of the second. .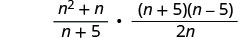
    Factor any expressions if possible. .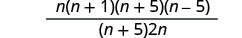
    Remove common factors. .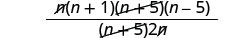
    Simplify. .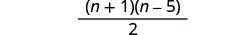
    Example \(\PageIndex{11}\)

    \(\frac{b−\frac{3b}{b+5}}{\frac{2}{b+5}+\frac{1}{b−5}}\).

    Answer

    b(b+2)

    Example \(\PageIndex{12}\)

    \(\frac{1−\frac{3}{c+4}}{\frac{1}{c+4}+\frac{c}{3}}\).

    Answer

    3c+3

    Simplify a Complex Rational Expression by Using the LCD

    We “cleared” the fractions by multiplying by the LCD when we solved equations with fractions. We can use that strategy here to simplify complex rational expressions. We will multiply the numerator and denominator by LCD of all the rational expressions.

    Let’s look at the complex rational expression we simplified one way in Example. We will simplify it here by multiplying the numerator and denominator by the LCD. When we multiply by \(\frac{LCD}{LCD}\) we are multiplying by 1, so the value stays the same.

    Example \(\PageIndex{13}\)

    Simplify: \(\frac{\frac{1}{3}+\frac{1}{6}}{\frac{1}{2}−\frac{1}{3}}\).

    Answer
      .
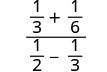
    The LCD of all the fractions in the whole expression is 6.  
    Clear the fractions by multiplying the numerator and denominator by that LCD. .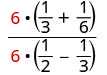
    Distribute. .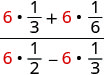
    Simplify. .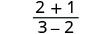
      .
      .
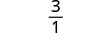
    Example \(\PageIndex{14}\)

    Simplify: \(\frac{\frac{1}{2}+\frac{1}{5}}{\frac{1}{10}+\frac{1}{5}}\).

    Answer

    \(\frac{7}{3}\)

    Example \(\PageIndex{15}\)

    Simplify: \(\frac{\frac{1}{4}+\frac{3}{8}}{\frac{1}{2}−\frac{5}{16}}\).

    Answer

    \(\frac{7}{3}\)

    How to Simplify a Complex Rational Expression by Using the LCD

    Example \(\PageIndex{16}\)

    Simplify: \(\frac{\frac{1}{x}+\frac{1}{y}}{\frac{x}{y}−\frac{y}{x}}\).

    Answer

    The above image has 3 columns. It shows the steps on how to simplify a complex rational expression using the LCD for 1 divided by x plus 1 divided by y divided by x divided by y minus y divided by x. Step one is to find the LCD of all fractions in the complex rational expression. The LCD of all the fractions is x y. Multiply the numerator and denominator by the LCD.Step two is to multiply both the numerator and denominator by x y to get x y times 1 divided by x plus 1 divided by y divided x y times x divided by y minus y divided by x.Step three is to simplify the expression. Distribute to get x y times 1 divided by x plus x y times 1 divided y divided by x y times x divided by y minus x y times y divided by x. Simplify to get y plus x divided by x squared minus y squared. Remove common factors. Cross out y plus x in the numerator. Cross out x plus y in the numerator. Simplify to get 1 divided by x minus y.

    Example \(\PageIndex{17}\)

    Simplify: \(\frac{\frac{1}{a}+\frac{1}{b}}{\frac{a}{b}−\frac{b}{a}}\).

    Answer

    \(\frac{b+a}{a^2+b^2}\)

    Example \(\PageIndex{18}\)

    Simplify: \(\frac{\frac{1}{x^2}−\frac{1}{y^2}}{\frac{1}{x}−\frac{1}{y}}\).

    Answer

    \(\frac{y−x}{xy}\)

    Definition: SIMPLIFY A COMPLEX RATIONAL EXPRESSION BY USING THE LCD.
    1. Find the LCD of all fractions in the complex rational expression.
    2. Multiply the numerator and denominator by the LCD.
    3. Simplify the expression.

    Be sure to start by factoring all the denominators so you can find the LCD.

    Example \(\PageIndex{19}\)

    Simplify: \(\frac{\frac{2}{x+6}}{\frac{4}{x−6}−\frac{4}{x^2−36}}\).

    Answer
      .
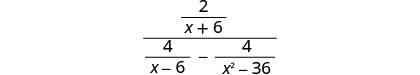
    Find the LCD of all fractions in the complex rational expression. The LCD is (x+6)(x−6)  
    Multiply the numerator and denominator by the LCD. .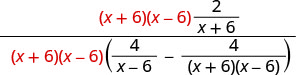
    Simplify the expression.  
    Distribute in the denominator. .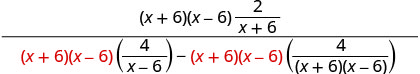
    Simplify. .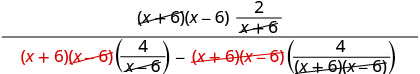
    Simplify. .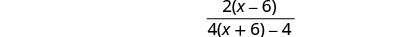
    To simplify the denominator, distribute and combine like terms. .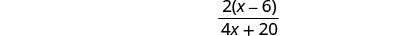
    Remove common factors. .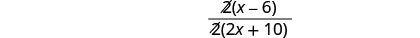
    Simplify. .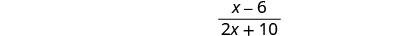
    Notice that there are no more factors common to the numerator and denominator.  
    Example \(\PageIndex{20}\)

    Simplify: \(\frac{\frac{3}{x+2}}{\frac{5}{x−2}−\frac{3}{x^2−4}}\).

    Answer

    \(\frac{3x−6}{5x+7}\)

    Example \(\PageIndex{21}\)

    Simplify: \(\frac{\frac{2}{x−7}−\frac{1}{x+7}}{\frac{6}{x+7}−\frac{1}{x^2−49}}\).

    Answer

    \(\frac{x+21}{6x+43}\)

    Example \(\PageIndex{22}\)

    Simplify: \(\frac{\frac{4}{m^2−7m+12}}{\frac{3}{m−3}−\frac{2}{m−4}}\).

    Answer
      .
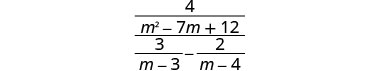
    Find the LCD of all fractions in the complex rational expression. The LCD is (m−3)(m−4)  
    Multiply the numerator and denominator by the LCD. .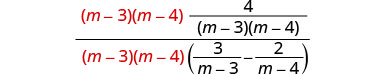
    Simplify. .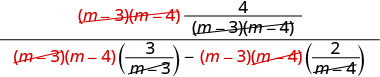
    Simplify. .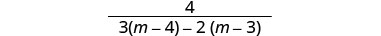
    Distribute. .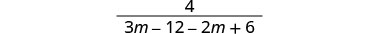
    Combine like terms. .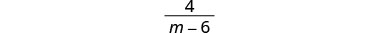
    Example \(\PageIndex{23}\)

    Simplify: \(\frac{\frac{3}{x^2+7x+10}}{\frac{4}{x+2}+\frac{1}{x+5}}\).

    Answer

    \(\frac{3}{5x+22}\)

    Example \(\PageIndex{24}\)

    Simplify: \(\frac{\frac{4y}{y+5}+\frac{2}{y+6}}{\frac{3y}{y^2+11y+30}}\).

    Answer

    \(\frac{6y+34}{3y}\)

    Example \(\PageIndex{25}\)

    Simplify: \(\frac{\frac{y}{y+1}}{1+\frac{1}{y−1}}\).

    Answer
      .
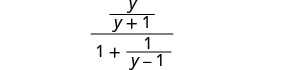
    Find the LCD of all fractions in the complex rational expression.  
    The LCD is (y+1)(y−1)  
    Multiply the numerator and denominator by the LCD. .
    Distribute in the denominator and simplify. .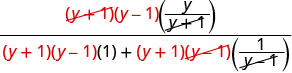
    Simplify. .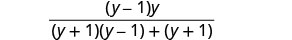
    Simplify the denominator, and leave the numerator factored. .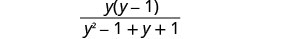
      .
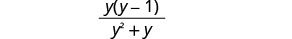
    Factor the denominator, and remove factors common with the numerator. .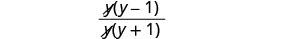
    Simplify. .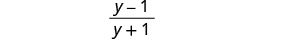
    Example \(\PageIndex{26}\)

    Simplify: \(\frac{\frac{x}{x+3}}{1+\frac{1}{x+3}}\).

    Answer

    \(\frac{x}{x+4}\)

    Example \(\PageIndex{27}\)

    Simplify: \(\frac{1+\frac{1}{x−1}}{\frac{3}{x+1}}\).

    Answer

    \(\frac{x(x+1)}{3(x−1)}\)

    Key Concepts

    • To Simplify a Rational Expression by Writing it as Division
      1. Simplify the numerator and denominator.
      2. Rewrite the complex rational expression as a division problem.
      3. Divide the expressions.
    • To Simplify a Complex Rational Expression by Using the LCD
      1. Find the LCD of all fractions in the complex rational expression.
      2. Multiply the numerator and denominator by the LCD.
      3. Simplify the expression.

    Glossary

    complex rational expression
    A complex rational expression is a rational expression in which the numerator or denominator contains a rational expression.

    This page titled 8.5: Simplify Complex Rational Expressions is shared under a CC BY-NC-SA license and was authored, remixed, and/or curated by OpenStax.