6.6: Graph Theory

Last updated
Save as PDF

Page ID: 51604

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

In the modern world, planning efficient routes is essential for business and industry, with applications as varied as product distribution, laying new fiber optic lines for broadband internet, and suggesting new friends within social network websites like Facebook.

This field of mathematics started nearly 300 years ago as a look into a mathematical puzzle (we’ll look at it in a bit). The field has exploded in importance in the last century, both because of the growing complexity of business in a global economy and because of the computational power that computers have provided us.

Drawing Graphs

Example 1

Here is a portion of a housing development from Missoula, Montana. As part of her job, the development’s lawn inspector has to walk down every street in the development making sure homeowners’ landscaping conforms to the community requirements.

$Fig2_5_1$

Naturally, she wants to minimize the amount of walking she has to do. Is it possible for her to walk down every street in this development without having to do any backtracking? While you might be able to answer that question just by looking at the picture for a while, it would be ideal to be able to answer the question for any picture regardless of its complexity.

To do that, we first need to simplify the picture into a form that is easier to work with. We can do that by drawing a simple line for each street. Where streets intersect, we will place a dot.

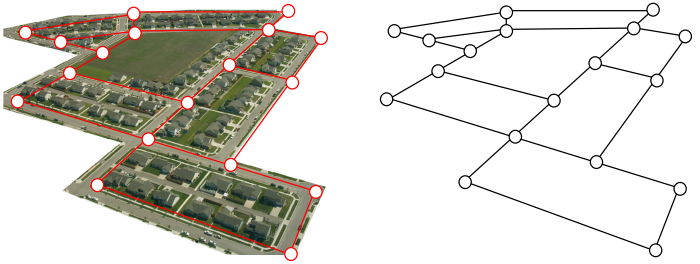
$Fig2_5_2$

This type of simplified picture is called a graph.

Graphs, Vertices, and Edges

A graph consists of a set of dots, called vertices, and a set of edges connecting pairs of vertices.

While we drew our original graph to correspond with the picture we had, there is nothing particularly important about the layout when we analyze a graph. Both of the graphs below are equivalent to the one drawn above.

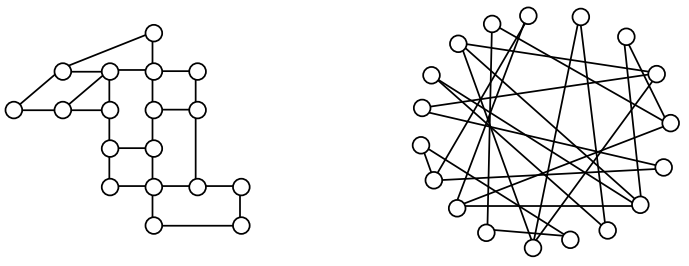
$Fig2_5_3$

You probably already noticed that we are using the term graph differently than you may have used the term in the past to describe the graph of a mathematical function.

Example 2

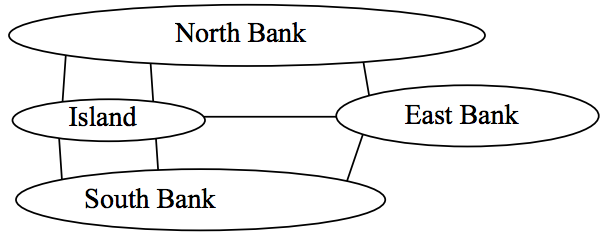
$Fig2_5_4$ Back in the 18th century in the Prussian city of Königsberg, a river ran through the city and seven bridges crossed the forks of the river. The river and the bridges are highlighted in the picture to the right.^[1]

As a weekend amusement, townsfolk would see if they could find a route that would take them across every bridge once and return them to where they started.

Leonard Euler (pronounced OY-lur), one of the most prolific mathematicians ever, looked at this problem in 1735, laying the foundation for graph theory as a field in mathematics. To analyze this problem, Euler introduced edges representing the bridges:

$Fig2_5_5$

Since the size of each land mass it is not relevant to the question of bridge crossings, each can be shrunk down to a vertex representing the location:

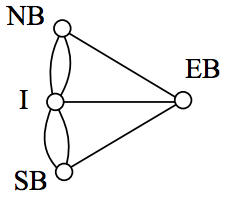
$Fig2_5_6$

Notice that in this graph there are two edges connecting the north bank and island, corresponding to the two bridges in the original drawing. Depending upon the interpretation of edges and vertices appropriate to a scenario, it is entirely possible and reasonable to have more than one edge connecting two vertices.

While we haven’t answered the actual question yet of whether or not there is a route which crosses every bridge once and returns to the starting location, the graph provides the foundation for exploring this question.

Definitions

While we loosely defined some terminology earlier, we now will try to be more specific.

Vertex

A vertex is a dot in the graph that could represent an intersection of streets, a land mass, or a general location, like “work” or “school”. Vertices are often connected by edges. Note that vertices only occur when a dot is explicitly placed, not whenever two edges cross. Imagine a freeway overpass—the freeway and side street cross, but it is not possible to change from the side street to the freeway at that point, so there is no intersection and no vertex would be placed.

Edges

Edges connect pairs of vertices. An edge can represent a physical connection between locations, like a street, or simply that a route connecting the two locations exists, like an airline flight.

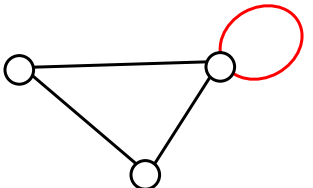
Loop

A loop is a special type of edge that connects a vertex to itself. Loops are not used much in street network graphs.

$Fig2_5_7$

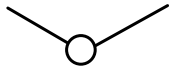
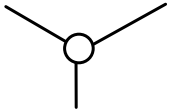
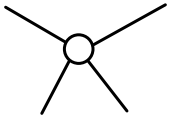
Degree of a vertex

The degree of a vertex is the number of edges meeting at that vertex. It is possible for a vertex to have a degree of zero or larger.

Degree 0	Degree 1	Degree 2	Degree 3	Degree 4
$Fig2_5_8$	$Fig2_5_9$	$Fig2_5_10$	$Fig2_5_11$	$Fig2_5_12$

Path

A path is a sequence of vertices using the edges. Usually we are interested in a path between two vertices. For example, a path from vertex A to vertex M is shown below. It is one of many possible paths in this graph.

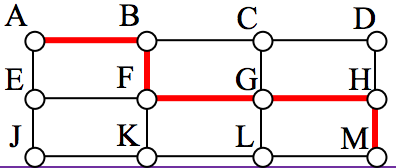
$Fig2_5_13$

Circuit

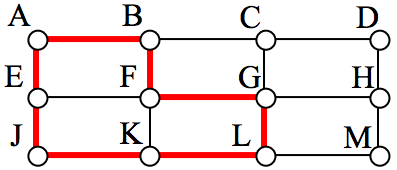
A circuit is a path that begins and ends at the same vertex. A circuit starting and ending at vertex A is shown below.

$Fig2_5_14$

Connected

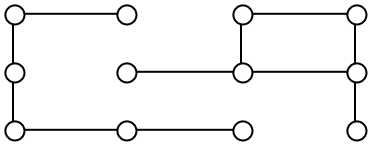
A graph is connected if there is a path from any vertex to any other vertex. Every graph drawn so far has been connected. The graph below is disconnected; there is no way to get from the vertices on the left to the vertices on the right.

$Fig2_5_15$

Weights

Depending upon the problem being solved, sometimes weights are assigned to the edges. The weights could represent the distance between two locations, the travel time, or the travel cost. It is important to note that the distance between vertices in a graph does not necessarily correspond to the weight of an edge.

Euler Circuits and the Chinese Postman Problem

In the first section, we created a graph of the Königsberg bridges and asked whether it was possible to walk across every bridge once. Because Euler first studied this question, these types of paths are named after him.

Euler Path

An Euler path is a path that uses every edge in a graph with no repeats. Being a path, it does not have to return to the starting vertex.

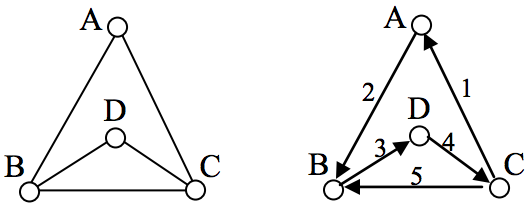
Example 3

In the graph shown below, there are several Euler paths. One such path is CABDCB. The path is shown in arrows to the right, with the order of edges numbered.

$Fig2_5_16$

Euler Circuit

An Euler circuit is a circuit that uses every edge in a graph with no repeats. Being a circuit, it must start and end at the same vertex.

Example 4

The graph below has several possible Euler circuits. Here’s a couple, starting and ending at vertex A: ADEACEFCBA and AECABCFEDA. The second is shown in arrows.

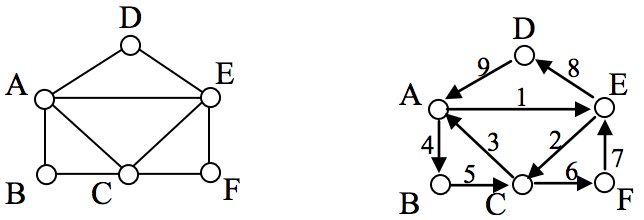
$Fig2_5_17$

Look back at the example used for Euler paths—does that graph have an Euler circuit? A few tries will tell you no; that graph does not have an Euler circuit. When we were working with shortest paths, we were interested in the optimal path. With Euler paths and circuits, we’re primarily interested in whether an Euler path or circuit exists.

Why do we care if an Euler circuit exists? Think back to our housing development lawn inspector from the beginning of the chapter. The lawn inspector is interested in walking as little as possible. The ideal situation would be a circuit that covers every street with no repeats. That’s an Euler circuit! Luckily, Euler solved the question of whether or not an Euler path or circuit will exist.

Euler’s Path and Circuit Theorems

A graph will contain an Euler path if it contains at most two vertices of odd degree.

A graph will contain an Euler circuit if all vertices have even degree

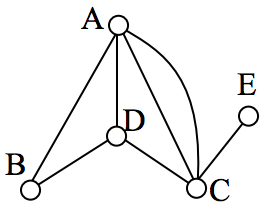
Example 5

In the graph below, vertices A and C have degree 4, since there are 4 edges leading into each vertex. B is degree 2, D is degree 3, and E is degree 1. This graph contains two vertices with odd degree (D and E) and three vertices with even degree (A, B, and C), so Euler’s theorems tell us this graph has an Euler path, but not an Euler circuit.

$Fig2_5_18$

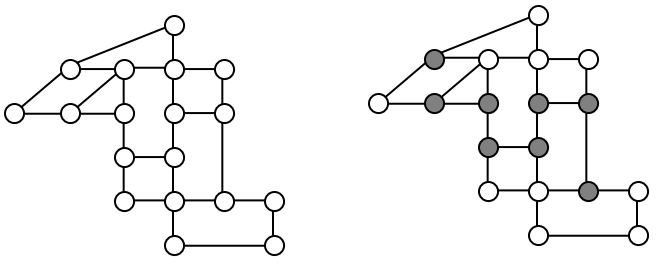
Example 6

Is there an Euler circuit on the housing development lawn inspector graph we created earlier in the chapter? All the highlighted vertices have odd degree. Since there are more than two vertices with odd degree, there are no Euler paths or Euler circuits on this graph. Unfortunately our lawn inspector will need to do some backtracking.

$Fig2_5_19$

Example 7

When it snows in the same housing development, the snowplow has to plow both sides of every street. For simplicity, we’ll assume the plow is out early enough that it can ignore traffic laws and drive down either side of the street in either direction. This can be visualized in the graph by drawing two edges for each street, representing the two sides of the street.

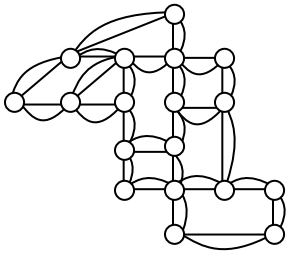
$Fig2_5_20$

Notice that every vertex in this graph has even degree, so this graph does have an Euler circuit.

Bogdan Giuşcă. http://en.wikipedia.org/wiki/File:Konigsberg_bridges.png ↵

Graph Theory. Authored by: David Lippman. Located at: http://www.opentextbookstore.com/mathinsociety/. Project: Math in Society. License: CC BY: Attribution
Pleasant View housing development. Authored by: Sam Beebe. Located at: https://flic.kr/p/5kTroZ. License: CC BY: Attribution