19.2: M1.02- Power Models Part I
( \newcommand{\kernel}{\mathrm{null}\,}\)
Section 1: Dimensional relationships—the Power model 
Processes in which the relationship of input to output depends on volume, area, or distance often can be modeled by formulas in which output is computed by raising the input variable to a particular exponent power, then multiplying the result by a scaling factor. This differs from the earlier exponential formula because here the exponent is a parameter rather than being the input variable x, while x is used as the base rather than the exponent.
In addition to obvious relationships such as those between size, area, and volume for geometric shapes, power-function models are useful for many situations where the geometry involved is indirect. The rate at which animals use food, for example, depends on size based on interactions between weight (which grows rapidly with size) and breathing rate (which slows down), resulting in power-function relationships with fractional powers. The concentration of a fixed amount of a chemical dissolved in water has the reciprocal power-function relationship (where the power equals –1) to the amount of water. If the power equals exactly 1, the power function is a straight line through the origin; if the power is exactly 2, the power function is a parabola whose vertex is at the origin.
The power parameter may have any value, including fractional and negative numbers. However, for fractional powers (such as the x0.5 for square roots) power functions are well-defined only for values of x that are greater than or equal to zero. The scale parameter can be any value, although it is usually positive (a zero value will make all output values zero and a negative value will flip all values around the x axis); the effect of the scale parameter is to uniformly stretch or shrink the graph vertically.
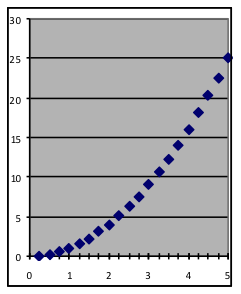 | 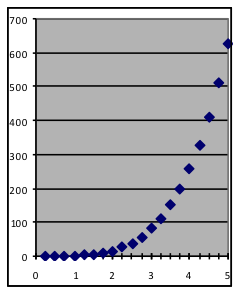 | 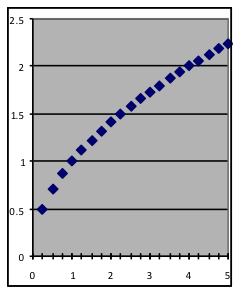 |
| Power models can take many shapes, depending on the value of the power. | ||
Examples of power-formula models:
y = 122.3 x0.667 predicts the surface area of a steel ball in mm2 based on its mass in grams.
y = 0.018 x3 predicts the weight of a cantaloupe in pounds based on its diameter in inches.
y = 2×108 x-1 predicts daily visitors to web sites based on the order of popularity of the sites.
y = 1.80 x0.667 predicts a planet’s orbit radius in miles based on the length of its year in days.
The process of fitting a power model to a dataset is the same as for the other models you have studied—put the data into a worksheet in Models.xls, then use Solver to find the best-fit parameters. But in this case you will not have a preset worksheet template in which C3 already contains the right kind of formula. Instead, you will need to make a modeling worksheet yourself, or modify a copy of one of the ones you used earlier in Models.xls. The description below assumes that you will use the same row and column numbers as in Model.xls for the same kind of purposes, although you may vary them as long as you do so consistently.
- Mathematics for Modeling. Authored by: Mary Parker and Hunter Ellinger. License: CC BY: Attribution

