7.1: Finding Composite and Inverse Functions
- Last updated
- Dec 16, 2019
- Save as PDF
- Page ID
- 29084
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Find and evaluate composite functions
- Determine whether a function is one-to-one
- Find the inverse of a function
Before you get started, take this readiness quiz.
- If f(x)=2x−3 and g(x)=x2+2x−3, find f(4).
If you missed this problem, review Example 3.48. - Solve for x, 3x+2y=12.
If you missed this problem, review Example 2.31. - Simplify: 5(x+4)5−4.
If you missed this problem, review Example 1.25.
In this chapter, we will introduce two new types of functions, exponential functions and logarithmic functions. These functions are used extensively in business and the sciences as we will see.
Find and Evaluate Composite Functions
Before we introduce the functions, we need to look at another operation on functions called composition. In composition, the output of one function is the input of a second function. For functions f and g, the composition is written f∘g and is defined by (f∘g)(x)=f(g(x)).
We read f(g(x)) as “f of g of x.”
To do a composition, the output of the first function, g(x), becomes the input of the second function, f, and so we must be sure that it is part of the domain of f.
Definition 7.1.1
The composition of functions f and g is written f⋅g and is defined by
(f∘g)(x)=f(g(x))
We read f(g(x)) as f of g of x.
We have actually used composition without using the notation many times before. When we graphed quadratic functions using translations, we were composing functions. For example, if we first graphed g(x)=x2 as a parabola and then shifted it down vertically four units, we were using the composition defined by (f∘g)(x)=f(g(x)) where f(x)=x−4.
Example 7.1.1
For functions f(x)=4x−5 and g(x)=2x+3, find
- (f∘g)(x)
- (g∘f)(x)
- (f⋅g)(x)
Solution:
-
Use the definition of (f∘g)(x). 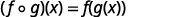

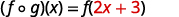

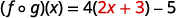
Distribute. 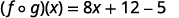
Simplify. 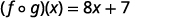
Table 10.1.1 -
Use the definition of (f∘g)(x). 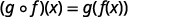

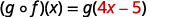

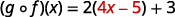
Distribute. 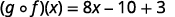
Simplify. 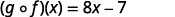
Table 10.1.2
Notice the difference in the result in part a. and part b.
c. Notice that (f⋅g)(x) is different than (f∘g)(x). In part a. we did the composition of the functions. Now in part c. we are not composing them, we are multiplying them.
Use the definition of (f⋅g)(x).
(f⋅g)(x)=f(x)⋅g(x)
Substitute f(x)=4x−5 and g(x)=2x+3.
(f⋅g)(x)=(4x−5)⋅(2x+3)
Multiply.
(f⋅g)(x)=8x2+2x−15
Exercise 7.1.1
For functions f(x)=3x−2 and g(x)=5x+1, find
- (f∘g)(x)
- (g∘f)(x)
- (f⋅g)(x)
- Answer
-
- 15x+1
- 15x−9
- 15x2−7x−2
Exercise 7.1.2
For functions f(x)=4x−3, and g(x)=6x−5, find
- (f∘g)(x)
- (g∘f)(x)
- (f⋅g)(x)
- Answer
-
- 24x−23
- 24x−23
- 24x2−38x+15
In the next example we will evaluate a composition for a specific value.
Example 7.1.2
For functions f(x)=x2−4, and g(x)=3x+2, find:
- (f∘g)(−3)
- (g∘f)(−1)
- (f∘f)(2)
Solution:
-
Use the definition of (f∘g)(−3). 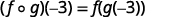

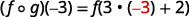
Simplify. 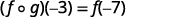

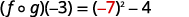
Simplify. 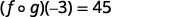
Table 10.1.3 -
Use the definition of (g∘f)(−1). 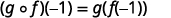

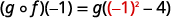
Simplify. 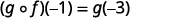

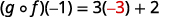
Simplify. 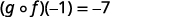
Table 10.1.4 -
Use the definition of (f∘f)(2). 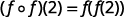

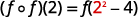
Simplify. 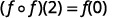

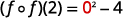
Simplify. 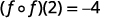
Table 10.1.5
Exercise 7.1.3
For functions f(x)=x2−9, and g(x)=2x+5, find
- (f∘g)(−2)
- (g∘f)(−3)
- (f∘f)(4)
- Answer
-
- −8
- 5
- 40
Exercise 7.1.4
For functions f(x)=x2+1, and g(x)=3x−5, find
- (f∘g)(−1)
- (g∘f)(2)
- (f∘f)(−1)
- Answer
-
- 65
- 10
- 5
Determine Whether a Function is One-to-One
When we first introduced functions, we said a function is a relation that assigns to each element in its domain exactly one element in the range. For each ordered pair in the relation, each x-value is matched with only one y-value.
We used the birthday example to help us understand the definition. Every person has a birthday, but no one has two birthdays and it is okay for two people to share a birthday. Since each person has exactly one birthday, that relation is a function.

A function is one-to-one if each value in the range has exactly one element in the domain. For each ordered pair in the function, each y-value is matched with only one x-value.
Our example of the birthday relation is not a one-to-one function. Two people can share the same birthday. The range value August 2 is the birthday of Liz and June, and so one range value has two domain values. Therefore, the function is not one-to-one.
Definition 7.1.2
A function is one-to-one if each value in the range corresponds to one element in the domain. For each ordered pair in the function, each y-value is matched with only one x-value. There are no repeated y-values.
Example 7.1.3
For each set of ordered pairs, determine if it represents a function and, if so, if the function is one-to-one.
- {(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}
- {(0,0),(1,1),(4,2),(9,3),(16,4)}
Solution:
- {(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}
Each x-value is matched with only one y-value. So this relation is a function.
But each y-value is not paired with only one x-value, (−3,27) and (3,27), for example. So this function is not one-to-one.
- {(0,0),(1,1),(4,2),(9,3),(16,4)}
Each x-value is matched with only one y-value. So this relation is a function.
Since each y-value is paired with only one x-value, this function is one-to-one.
Exercise 7.1.5
For each set of ordered pairs, determine if it represents a function and if so, is the function one-to-one.
- {(−3,−6),(−2,−4),(−1,−2),(0,0),(1,2),(2,4),(3,6)}
- {(−4,8),(−2,4),(−1,2),(0,0),(1,2),(2,4),(4,8)}
- Answer
-
- One-to-one function
- Function; not one-to-one
Exercise 7.1.6
For each set of ordered pairs, determine if it represents a function and if so, is the function one-to-one.
- {(27,−3),(8,−2),(1,−1),(0,0),(1,1),(8,2),(27,3)}
- {(7,−3),(−5,−4),(8,0),(0,0),(−6,4),(−2,2),(−1,3)}
- Answer
-
- Not a function
- Function; not one-to-one
To help us determine whether a relation is a function, we use the vertical line test. A set of points in a rectangular coordinate system is the graph of a function if every vertical line intersects the graph in at most one point. Also, if any vertical line intersects the graph in more than one point, the graph does not represent a function.
The vertical line is representing an x-value and we check that it intersects the graph in only one y-value. Then it is a function.
To check if a function is one-to-one, we use a similar process. We use a horizontal line and check that each horizontal line intersects the graph in only one point. The horizontal line is representing a y-value and we check that it intersects the graph in only one x-value. If every horizontal line intersects the graph of a function in at most one point, it is a one-to-one function. This is the horizontal line test.
Definition 7.1.3
Horizontal Line Test
If every horizontal line intersects the graph of a function in at most one point, it is a one-to-one function.
We can test whether a graph of a relation is a function by using the vertical line test. We can then tell if the function is one-to-one by applying the horizontal line test.
Example 7.1.4
Determine
- whether each graph is the graph of a function and, if so,
- whether it is one-to-one
Solution:
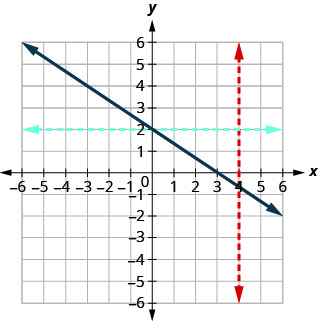
Figure 10.1.40
Since any vertical line intersects the graph in at most one point, the graph is the graph of a function. Since any horizontal line intersects the graph in at most one point, the graph is the graph of a one-to-one function.
b.
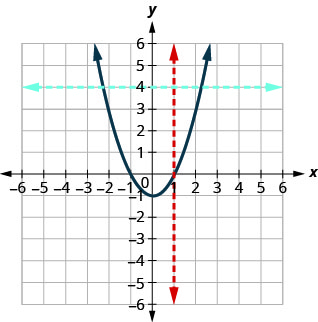
Since any vertical line intersects the graph in at most one point, the graph is the graph of a function. The horizontal line shown on the graph intersects it in two points. This graph does not represent a one-to-one function.
Exercise 7.1.7
Determine
- whether each graph is the graph of a function and, if so,
- whether it is one-to-one
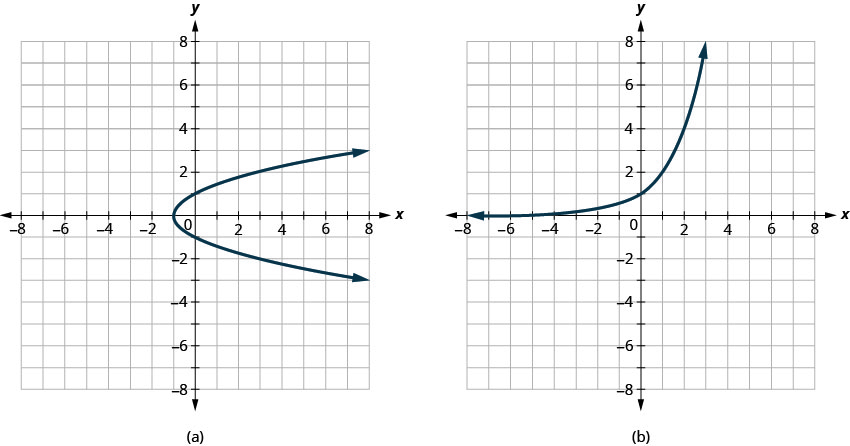
- Answer
-
- Not a function
- One-to-one function
Exercise 7.1.8
Determine
- whether each graph is the graph of a function and, if so,
- whether it is one-to-one
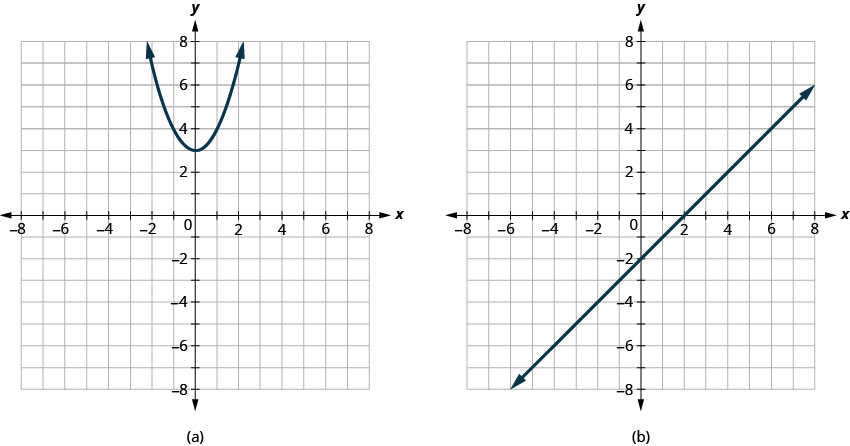
- Answer
-
- Function; not one-to-one
- One-to-one function
Find the Inverse of a Function
Let’s look at a one-to one function, f, represented by the ordered pairs {(0,5),(1,6),(2,7),(3,8)}. For each x-value, f adds 5 to get the y-value. To ‘undo’ the addition of 5, we subtract 5 from each y-value and get back to the original x-value. We can call this “taking the inverse of f” and name the function f−1.
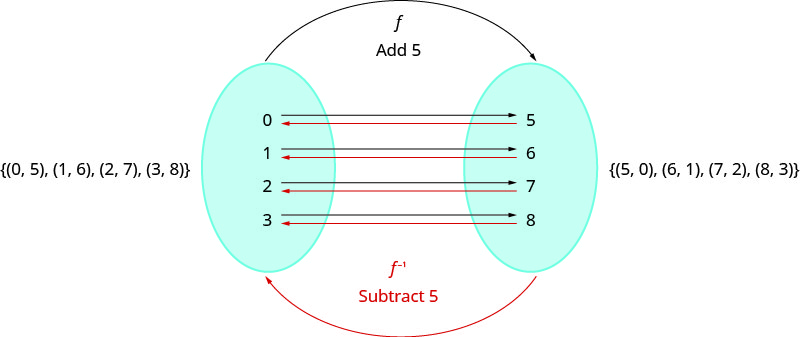
Notice that that the ordered pairs of f and f−1 have their x-values and y-values reversed. The domain of f is the range of f−1 and the domain of f−1 is the range of f.
Definition 7.1.4
Inverse of a Function Defined by Ordered Pairs
If f(x) is a one-to-one function whose ordered pairs are of the form (x,y), then its inverse function f−1(x) is the set of ordered pairs (y,x).
In the next example we will find the inverse of a function defined by ordered pairs.
Example 7.1.5
Find the inverse of the function {(0,3),(1,5),(2,7),(3,9)}. Determine the domain and range of the inverse function.
Solution:
This function is one-to-one since every x-value is paired with exactly one y-value.
To find the inverse we reverse the x-values and y-values in the ordered pairs of the function.
Function{(0,3),(1,5),(2,7),(3,9)}Inverse Function{(3,0),(5,1),(7,2),(9,3)}Domain of Inverse Function{3,5,7,9}Range of Inverse Function{0,1,2,3}
Exercise 7.1.9
Find the inverse of {(0,4),(1,7),(2,10),(3,13)}. Determine the domain and range of the inverse function.
- Answer
-
Inverse function: {(4,0),(7,1),(10,2),(13,3)}. Domain: {4,7,10,13}. Range: {0,1,2,3}.
Exercise 7.1.10
Find the inverse of {(−1,4),(−2,1),(−3,0),(−4,2)}. Determine the domain and range of the inverse function.
- Answer
-
Inverse function: {(4,−1),(1,−2),(0,−3),(2,−4)}. Domain: {0,1,2,4}. Range: {−4,−3,−2,−1}.
We just noted that if f(x) is a one-to-one function whose ordered pairs are of the form (x,y), then its inverse function f−1(x) is the set of ordered pairs (y,x).
So if a point (a,b) is on the graph of a function f(x), then the ordered pair (b,a) is on the graph of f−1(x). See Figure 10.1.43.
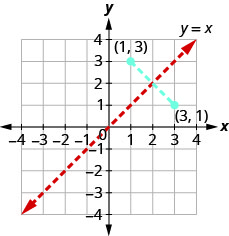
The distance between any two pairs (a,b) and (b,a) is cut in half by the line y=x. So we say the points are mirror images of each other through the line y=x.
Since every point on the graph of a function f(x) is a mirror image of a point on the graph of f−1(x), we say the graphs are mirror images of each other through the line y=x. We will use this concept to graph the inverse of a function in the next example.
Example 7.1.6
Graph, on the same coordinate system, the inverse of the one-to one function shown.
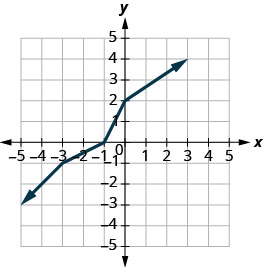
Solution:
We can use points on the graph to find points on the inverse graph. Some points on the graph are: (−5,−3),(−3,−1),(−1,0),(0,2),(3,4).
So, the inverse function will contain the points: (−3,−5),(−1,−3),(0,−1),(2,0),(4,3).
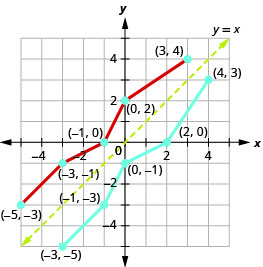
Notice how the graph of the original function and the graph of the inverse functions are mirror images through the line y=x.
Exercise 7.1.11
Graph, on the same coordinate system, the inverse of the one-to one function.
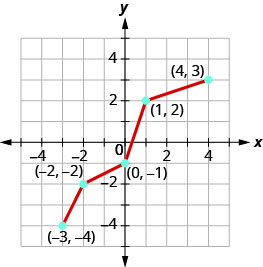
- Answer
-
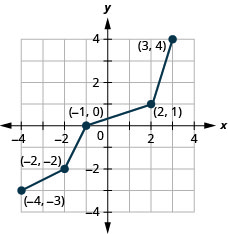
Figure 10.1.49
Exercise 7.1.12
Graph, on the same coordinate system, the inverse of the one-to one function.
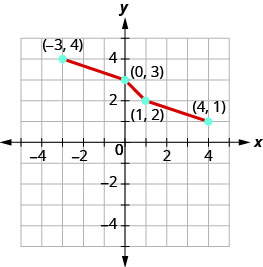
- Answer
-
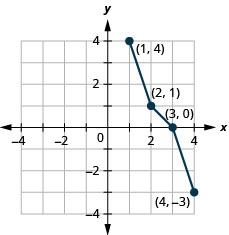
Figure 10.1.51
When we began our discussion of an inverse function, we talked about how the inverse function ‘undoes’ what the original function did to a value in its domain in order to get back to the original x-value.

Definition 7.1.5
Inverse Functions
f−1(f(x))=x, for all x in the domain of f
f(f−1(x))=x, for all x in the domain of f−1
We can use this property to verify that two functions are inverses of each other.
Example 7.1.7
Verify that f(x)=5x−1 and g(x)=x+15 are inverse functions.
Solution:
The functions are inverses of each other if g(f(x))=x and f(g(x))=x.
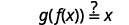 |
|
| Substitue 5x−1 for f(x). | 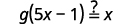 |
 |
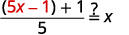 |
| Simplify. | 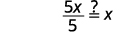 |
| Simplify. | 
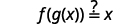
|
| Substitute x+15 for g(x). | 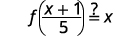 |
 |
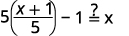 |
| Simplify. | 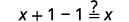 |
| Simplify. |  |
Since both g(f(x))=x and f(g(x))=x are true, the functions f(x)=5x−1 and g(x)=x+15 are inverse functions. That is, they are inverses of each other.
Exercise 7.1.13
Verify that the functions are inverse functions. f(x)=4x−3 and g(x)=x+34.
- Answer
-
g(f(x))=x, and f(g(x))=x, so they are inverses.
Exercise 7.1.14
Verify that the functions are inverse functions. f(x)=2x+6 and g(x)=x−62
- Answer
-
g(f(x))=x, and f(g(x))=x, so they are inverses.
We have found inverses of function defined by ordered pairs and from a graph. We will now look at how to find an inverse using an algebraic equation. The method uses the idea that if f(x) is a one-to-one function with ordered pairs (x,y), then its inverse function f−1(x) is the set of ordered pairs (y,x).
If we reverse the x and y in the function and then solve for y, we get our inverse function.
Example 7.1.8 How to Find the Inverse of a One-to-One Function
Find the inverse of f(x)=4x+7.
Solution:
| Step 1. Substitute y for f(x). | Replace f(x) with y. | f(x)=4x+7y=4x+7 |
| Step 2: Interchange the variables x and y. | Replace x with y and then y with x. | x=4y+7 |
| Step 3: Solve for y. |
Subtract 7 from each side. Divide by 4. |
x−7=4y x−74=y |
| Step 4: Substitute f−1(x) for y. | Replace y with f−1(x). | x−74=f−1(x) |
| Step 5: Verify that the functions are inverses. |
Show f−1(f(x))=x and f(f−1(x))=x |
f−1(f(x))?=xf−1(4x+7)?=x(4x+7)−74?=x4x4?=xx=xf(f−1(x))?=xf(x−74)?=x4(x−74)+7?=xx−7+7?=xx=x |
Exercise 7.1.15
Find the inverse of the function f(x)=5x−3.
- Answer
-
f−1(x)=x+35
Exercise 7.1.16
Find the inverse of the function f(x)=8x+5.
- Answer
-
f−1(x)=x−58
We summarize the steps below.
How to Find the Inverse of a One-to-One Function
- Substitute y for f(x).
- Interchange the variables x and y.
- Solve for y.
- Substitute f−1(x) for y.
- Verify that the functions are inverses.
Example 7.1.9 How to Find the Inverse of a One-to-One Function
Find the inverse of f(x)=5√2x−3.
Solution:
f(x)=5√2x−3
Substitute y for f(x).
y=5√2x−3
Interchange the variables x and y.
x=5√2y−3
Solve for y.
(x)5=(5√2y−3)5x5=2y−3x5+3=2yx5+32=y
Substitute f−1(x) for y.
f−1(x)=x5+32
Verify that the functions are inverses.
f−1(f(x))?=xf(f−1(x))?=xf−1(5√2x−3)?=xf(x5+32)?=x(5√2x−3)5+32?=x5√2(x5+32)−3?=x2x−3+32?=x5√x5+3−3?=x2x2?=x5√x5?=xx=xx=x
Exercise 7.1.17
Find the inverse of the function f(x)=5√3x−2.
- Answer
-
f−1(x)=x5+23
Exercise 7.1.18
Find the inverse of the function f(x)=4√6x−7.
- Answer
-
f−1(x)=x4+76
Key Concepts
- Composition of Functions: The composition of functions f and g, is written f∘g and is defined by
(f∘g)(x)=f(g(x))
We read f(g(x)) as f of g of x. - Horizontal Line Test: If every horizontal line, intersects the graph of a function in at most one point, it is a one-to-one function.
- Inverse of a Function Defined by Ordered Pairs: If f(x) is a one-to-one function whose ordered pairs are of the form (x,y), then its inverse function f−1(x) is the set of ordered pairs (y,x).
- Inverse Functions: For every x in the domain of one-to-one function f and f−1,
f−1(f(x))=x
f(f−1(x))=x - How to Find the Inverse of a One-to-One Function:
- Substitute y for f(x).
- Interchange the variables x and y.
- Solve for y.
- Substitute f−1(x) for y.
- Verify that the functions are inverses.
Glossary
- one-to-one function
- A function is one-to-one if each value in the range has exactly one element in the domain. For each ordered pair in the function, each y-value is matched with only one x-value.


