9.2: Arithmetic Sequences

Last updated

Dec 16, 2019
Save as PDF
- 9.1: Sequences
- 9.3: Geometric Sequences and Series

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

By the end of this section, you will be able to:

Determine if a sequence is arithmetic
Find the general term ( $n$ th term) of an arithmetic sequence
Find the sum of the first $n$ terms of an arithmetic sequence

Before you get started, take this readiness quiz.

Evaluate $4n−1$ for the integers $1, 2, 3$ , and $4$ .
If you missed this problem, review Example 1.6.
Solve the system of equations: $\left\{\begin{array}{l}{x+y=7} \\ {3 x+4 y=23}\end{array}\right.$ .
If you missed this problem, review Example 4.9.
If $f(n)=\frac{n}{2}(3 n+5)$ , find $f(1)+f(20)$ .
If you missed this problem, review Example 3.49.

Determine if a Sequence is Arithmetic

The last section introduced sequences and now we will look at two specific types of sequences that each have special properties. In this section we will look at arithmetic sequences and in the next section, geometric sequences.

An arithmetic sequence is a sequence where the difference between consecutive terms is constant. The difference between consecutive terms in an arithmetic sequence, a_{n}-a_{n-1}, is $d$ , the common difference, for $n$ greater than or equal to two.

Definition $\PageIndex{1}$

An arithmetic sequence is a sequence where the difference between consecutive terms is always the same.

The difference between consecutive terms, a_{n}-a_{n-1}, is $d$ , the common difference, for $n$ greater than or equal to two.

This figure has two rows and three columns. The first row reads “7”, “10”,”13”, “16”, “19”, “22”, and an ellipsis, “10 minus 7, divided by 3”, “13 minus 10, divided by 3”, “16 minus 13, divided by 3”, nth term equals nth term minus 1 divided by d” — Figure 12.2.1

Example $\PageIndex{1}$

Determine if each sequence is arithmetic. If so, indicate the common difference.

$5,9,13,17,21,25, \dots$
$4,9,12,17,20,25, \dots$
$10,3,-4,-11,-18,-25, \dots$

Solution:

To determine if the sequence is arithmetic, we find the difference of the consecutive terms shown.

a. $\begin{array}{cccccc}{5,} & {9,} & {13,} & {17} & {21,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-5} & {13-9} & {17-13} & {21-17} & {25-21} \\ & {4} & {4} & {4} & {4}&{4}\end{array}$

The sequence is arithmetic. The common difference is $d=4$ .

b. $\begin{array}{cccccc}{4,} & {9,} & {12,} & {17} & {20,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-4} & {12-9} & {17-12} & {20-17} & {25-20} \\ & {2} & {3} & {5} & {3}&{5}\end{array}$

The sequence is not arithmetic as all the differences between the consecutive terms are not the same. There is no common difference.

c. $\begin{array}{cccccc}{10,} & {3,} & {-4,} & {-11} & {-18,} & {-25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {3-10} & {-4-3} & {-11-(-4)} & {-18-(-11)} & {-25-(-18)} \\ & {-7} & {-7} & {-7} & {-7}&{-7}\end{array}$

Answer:

The sequence is arithmetic. The common difference is $d=-7$ .

Exercise $\PageIndex{1}$

Determine if each sequence is arithmetic. If so, indicate the common difference.

$9,20,31,42,53,64, \dots$
$12,6,0,-6,-12,-18, \dots$
$7,1,10,4,13,7, \dots$

Answer

The sequence is arithmetic with common difference $d=11$ .
The sequence is arithmetic with common difference $d=-6$ .
The sequence is not arithmetic as all the differences between the consecutive terms are not the same.

Exercise $\PageIndex{2}$

Determine if each sequence is arithmetic. If so, indicate the common difference.

$-4,4,2,10,8,16, \dots$
$-3,-1,1,3,5,7, \dots$
$7,2,-3,-8,-13,-18, \dots$

Answer

The sequence is not arithmetic as all the differences between the consecutive terms are not the same.
The sequence is arithmetic with common difference $d=2$ .
The sequence is arithmetic with common difference $d=−5$ .

If we know the first term, $a_{1}$ , and the common difference, $d$ , we can list a finite number of terms of the sequence.

Example $\PageIndex{2}$

Write the first five terms of the sequence where the first term is $5$ and the common difference is $d=−6$ .

Solution:

We start with the first term and add the common difference. Then we add the common difference to that result to get the next term, and so on.

$\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {5} & {5+(-6)} & {-1+(-6)} & {-7+(-6)} & {-13+(-6)} \\ {}&{-1} & {-7} & {-13} & {-19}\end{array}$

Answer:

The sequence is $5,-1,-7,-13,-19, \dots$

Exercise $\PageIndex{3}$

Write the first five terms of the sequence where the first term is $7$ and the common difference is $d=−4$ .

Answer: $7,3,-1,-5,-9, \dots$

Exercise $\PageIndex{4}$

Write the first five terms of the sequence where the first term is $11$ and the common difference is $d=−8$ .

Answer: $11,3,-5,-13,-21, \dots$

Find the General Term ( $n$ th Term) of an Arithmetic Sequence

Just as we found a formula for the general term of a sequence, we can also find a formula for the general term of an arithmetic sequence.

Let’s write the first few terms of a sequence where the first term is $a_{1}$ and the common difference is $d$ . We will then look for a pattern.

As we look for a pattern we see that each term starts with $a_{1}$ .

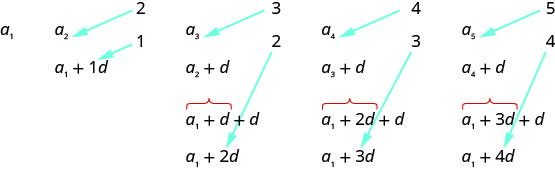
This figures shows an image of a sequence. — Figure 12.2.2

The first term adds $0d$ to the $a_{1}$ , the second term adds $1d$ , the third term adds $2d$ , the fourth term adds $3d$ , and the fifth term adds $4d$ . The number of $ds$ that were added to $a_{1}$ is one less than the number of the term. This leads us to the following

$a_{n}=a_{1}+(n-1) d$

Definition $\PageIndex{2}$

The general term of an arithmetic sequence with first term $a_{1}$ and the common difference $d$ is

$a_{n}=a_{1}+(n-1) d$

We will use this formula in the next example to find the 15^th term of a sequence.

Example $\PageIndex{3}$

Find the fifteenth term of a sequence where the first term is $3$ and the common difference is $6$ .

Solution:

$\begin{array}{cc}{\text{To find the fifteenth term, }a_{15}\text{, use the formula with } a_{1}=3 \:\text{and} \:d=6.}&{a_{n}=a_{1}+(n-1) d} \\ {\text{Substitute in the values.}}&{a_{15}=3+(15-1) 6} \\{\text{Simplify.}}& {a_{15}=3+(14) 6} \\ {}&{a_{15}=87}\end{array}$

Exercise $\PageIndex{5}$

Find the twenty-seventh term of a sequence where the first term is $7$ and the common difference is $9$ .

Answer: $241$

Exercise $\PageIndex{6}$

Find the eighteenth term of a sequence where the first term is $13$ and the common difference is $−7$ .

Answer: $-106$

Sometimes we do not know the first term and we must use other given information to find it before we find the requested term.

Example $\PageIndex{4}$

Find the twelfth term of a sequence where the seventh term is $10$ and the common difference is $−2$ . Give the formula for the general term.

Solution:

To first find the first term, $a_{1}$ , use the formula with $a_{7}=10$ , $n=7$ , and $d=−2$ . Substitute in the values. Simplify.

$a_{n}=a_{1}+(n-1) d$
$10=a_{1}+(7-1)(-2)$
$10=a_{1}+(6)(-2)$
$10=a_{1}-12$
$a_{1}=22$

Find the twelfth term, $a_{12}$ ,using the formula with $a_{1}=22$ , $n=12$ , and $d=-2$ . Substitute in the values. Simplify.

$a_{n}=a_{1}+(n-1) d$
$a_{12}=22+(12-1)(-2)$
$a_{12}=22+(11)(-2)$
$a_{12}=0$

The twelfth term of the sequence is $0, a_{12}=0$

To find the general term, substitute the values into the formula.

$a_{n}=a_{1}+(n-1) d$
$a_{n}=22+(n-1)(-2)$
$a_{n}=22-2 n+2$

Answer:
The general term is $a_{n}=-2 n+24$

Exercise $\PageIndex{7}$

Find the eleventh term of a sequence where the ninth term is $8$ and the common difference is $−3$ . Give the formula for the general term.

Answer: $a_{11}=2 .$ The general term is $a_{n}=-3 n+35$

Exercise $\PageIndex{8}$

Find the nineteenth term of a sequence where the fifth term is $1$ and the common difference is $−4$ .Give the formula for the general term.

Answer: $a_{19}=-55 .$ The general term is $a_{n}=-4 n+21$

Sometimes the information given leads us to two equations in two unknowns. We then use our methods for solving systems of equations to find the values needed.

Example $\PageIndex{5}$

Find the first term and common difference of a sequence where the fifth term is $19$ and the eleventh term is $37$ . Give the formula for the general term.

Solution:

Since we know two terms, we can make a system of equations using the formula for the general term.

Table 12.2.1
	$.$
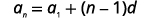We know the value of $a_{5}$ and $a_{11}$ , so we will use $n=5$ and $n=11$ .	$.$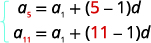
Substitute in the values, $a_{5}=19$ and $a_{11}=37$ .	$.$
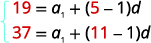Simplify.	$.$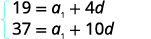
Prepare to eliminate the $a_{1}$ term by multiplying the top equation by $−1$ . Add the equations.	$.$
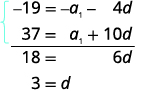Substituting $d=3$ back into the first equation.	$.$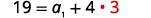
Solve for $a_{1}$ .	$.$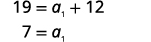
Use the formula with $a_{1}=7$ and $d=3$ .	$.$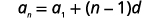
Substitute in the values.	$.$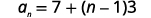
Simplify.	$.$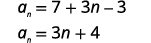
	The first term is $a_{1}=7$ . The common difference is $d=3$ .
	The general term of the sequence is $a_{n}=3n+4$ .

Answer:

The general term of the sequence is $a_{n}=3n+4$ .

Exercise $\PageIndex{9}$

Find the first term and common difference of a sequence where the fourth term is $17$ and the thirteenth term is $53$ . Give the formula for the general term.

Answer: $a_{1}=5, d=4 .$ The general term is $a_{n}=4 n+1$ .

Exercise $\PageIndex{10}$

Find the first term and common difference of a sequence where the third term is $2$ and the twelfth term is $−25$ . Give the formula for the general term.

Answer: $a_{1}=8, d=-3 .$ The general term is $a_{n}=-3 n+11$ .

Find the Sum of the First $n$ Terms of an Arithmetic Sequence

As with the general sequences, it is often useful to find the sum of an arithmetic sequence. The sum, $S_{n}$ , of the first $n$ terms of any arithmetic sequence is written as $S_{n} =a_{1} +a_{2} +a_{3} +\ldots +a_{n}$ . To find the sum by merely adding all the terms can be tedious. So we can also develop a formula to find the sum of a sequence using the first and last term of the sequence.

We can develop this new formula by first writing the sum by starting with the first term, $a_{1}$ , and keep adding a $d$ to get the next term as:

$S_{n}=a_{1}+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n}$ .

We can also reverse the order of the terms and write the sum by starting with $a_{n}$ and keep subtracting $d$ to get the next term as

$S_{n}=a_{n}+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1}$ .

If we add these two expressions for the sum of the first $n$ terms of an arithmetic sequence, we can derive a formula for the sum of the first $n$ terms of any arithmetic series.

$\begin{aligned} &S_{n}= a_{1} \quad+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n} \\+&S_{n} =a_{n} \quad+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1} \\ \hline \\ &2S_{n}=(a_{1}+a_{n})+(a_{1}+a_{n})+(a_{1}+a_{n})+\dots+(a_{1}+a_{n}) \end{aligned}$

Because there are $n$ sums of $(a_{1}+a_{n})$ on the right side of the equation, we rewrite the right side as $n(a_{1}+a_{n})$ .

$2 S_{n}=n\left(a_{1}+a_{n}\right)$

We divide by two to solve for $S_{n}$ .

$S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)$

This give us a general formula for the sum of the first $n$ terms of an arithmetic sequence.

Definition $\PageIndex{3}$

The sum, $S_{n}$ , of the first $n$ terms of an arithmetic sequence is

$S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)$

where $a_{1}$ is the first term and $a_{n}$ is the $n$ th term.

We apply this formula in the next example where the first few terms of the sequence are given.

Example $\PageIndex{6}$

Find the sum of the first $30$ terms of the arithmetic sequence: $8, 13, 18, 23, 28, …$

Solution:

To find the sum, we will use the formula $S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)$ . We know $a_{1}=8, d=5$ and $n=30$ , but we need to find $a_{n}$ in order to use the sum formula.

Find $a_{n}$ where $a_{1}=8, d=5$ and $n=30$ . Simplify.

$\begin{aligned} a_{n} &=a_{1}+(n-1) d \\ a_{30} &=8+(30-1) 5 \\ a_{30} &=8+(29) 5 \\ a_{30} &=153 \end{aligned}$

Knowing $a_{1}=8, n=30$ , and $a_{30}=153$ , use the sum formula. Substitute in the values. Simplify. Simplify.

$\begin{aligned} S_{n} &=\frac{n}{2}\left(a_{1}+a_{n}\right) \\ S_{30} &=\frac{30}{2}(8+153) \\ S_{30} &=15(161) \\ S_{30} &=2,415 \end{aligned}$

Exercise $\PageIndex{11}$

Find the sum of the first $30$ terms of the arithmetic sequence: $5, 9, 13, 17, 21, …$

Answer: $1,890$

Exercise $\PageIndex{12}$

Find the sum of the first $30$ terms of the arithmetic sequence: $7, 10, 13, 16, 19, …$

Answer: $1,515$

In the next example, we are given the general term for the sequence and are asked to find the sum of the first $50$ terms.

Example $\PageIndex{7}$

Find the sum of the first $50$ terms of the arithmetic sequence whose general term is $a_{n}=3n−4$ .

Solution:

To find the sum, we will use the formula $S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)$ . We know $n=50$ , but we need to find $a_{1}$ and $a_{n}$ in order to use the sum formula.

Table 12.2.2
	$.$
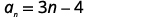Find $a_{1}$ , by substituting $n=1$ .	$.$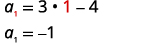
Find $a_{n}$ by substituting $n=50$ .	$.$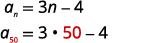
Simplify.	$.$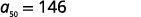
Knowing $n=50, a_{1}=−1,$ and $a_{50}=146$ use the sum formula.	$.$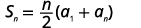
Substitute in the values.	$.$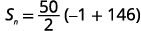
Simplify.	$.$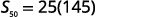
Simplify.	$.$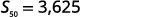

Exercise $\PageIndex{13}$

Find the sum of the first $50$ terms of the arithmetic sequence whose general term is $a_{n}=2n−5$ .

Answer: $2,300$

Exercise $\PageIndex{14}$

Find the sum of the first $50$ terms of the arithmetic sequence whose general term is $a_{n}=4n+3$ .

Answer: $5,250$

In the next example we are given the sum in summation notation. To add all the terms would be tedious, so we extract the information needed to use the formula to find the sum of the first $n$ terms.

Example $\PageIndex{8}$

Find the sum: $\sum_{i=1}^{25}(4 i+7)$ .

Solution:

To find the sum, we will use the formula $S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)$ . We know $n=25$ , but we need to find $a_{1}$ and $a_{n}$ in order to use the sum formula.

Table 12.2.3
Expand the summation notation.	$.$ Figure 12.2.21
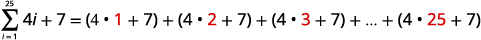
Simplify.	$.$ Figure 12.2.22
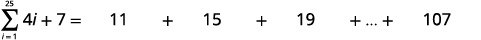
Identify $a_{1}$ .	$.$
Identify $a_{25}$ .	$.$ Figure 12.2.24
Knowing $n=25, a_{1}=11$ , and $a_{25} = 107$ use the sum formula.	$.$
Substitute in the values.	$.$
Simplify.	$.$
Simplify.	$.$

Exercise $\PageIndex{15}$

Find the sum: $\sum_{i=1}^{30}(6 i-4)$ .

Answer: $2,670$

Exercise $\PageIndex{16}$

Find the sum: $\sum_{i=1}^{35}(5 i-3)$ .

Answer: $3,045$

Access these online resources for additional instruction and practice with arithmetic sequences

Key Concepts

General Term ( $n$ th term) of an Arithmetic Sequence
The general term of an arithmetic sequence with first term $a_{1}$ and the common difference $d$ is
$a_{n}=a_{1}+(n-1) d$
Sum of the First $n$ Terms of an Arithmetic Sequence
The sum, $S_{n}$ , of the first \ $n$ terms of an arithmetic sequence, where $a_{1}$ is the first term and $a_{n}$ is the $n$ th term is
$S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)$

Glossary

arithmetic sequence: An arithmetic sequence is a sequence where the difference between consecutive terms is constant.

common difference: The difference between consecutive terms in an arithmetic sequence, $a_{n}−a_{n−1}$ , is $d$ , the common difference, for $n$ greater than or equal to two.