2.2E: Limits of Functions Exercises

Last updated
Save as PDF

Page ID: 10101

$OpenStax.jpg$
Contributed by OpenStax
Mathematics at OpenStax CNX

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

2.2: The Limit of a Function

Estimating limits from TABLES

For the following exercises, consider the function $f(x)=\frac{∣x^2−1∣}{x−1}$ .

30) [T] Complete the following table for the function. Round your solutions to four decimal places.

$x$	$f(x)$	$x$	$f(x)$
0.9	a.	1.1	e.
0.99	b.	1.01	f.
0.999	c.	1.001	g.
0.9999	d.	1.0001	h.

31) What do your results in the preceding exercise indicate about the two-sided limit $\displaystyle \lim_{x→1}f(x)$? Explain your response.

Answer:

$\displaystyle \lim_{x \to 1}f(x)$ does not exist because

$\displaystyle \lim_{x \to 1^−}f(x)=−2$ ≠ $\displaystyle \lim_{x \to 1^+}f(x)=2$.

For the following exercises, consider the function $f(x)=(1+x)^{1/x}$.

32) [T] Make a table showing the values of f for $x=−0.01,−0.001,−0.0001,−0.00001$ and for $x=0.01,0.001,0.0001,0.00001$. Round your solutions to five decimal places.

$x$	$f(x)$	\(x)\	$f(x)$
-0.01	a.	0.01	e.
-0.001	b.	0.001	f.
-0.0001	c.	0.0001	g.
-0.00001	d.	0.00001	h.

33) What does the table of values in the preceding exercise indicate about the function $f(x)=(1+x)^{1/x}$?

Answer:: It appears that: $\displaystyle \lim_{x \to 0}(1+x)^{1/x}=2.7183$

34) To which mathematical constant does the limit in the preceding exercise appear to be getting closer?

In the following exercises, use the given values to set up a table to evaluate the limits. Round your solutions to eight decimal places.

35) [T] $\displaystyle \lim_{x \to 0}\frac{\sin(2x)}{x};±0.1,±0.01,±0.001,±.0001$

$x$	$\frac{sin2x}{x}$	$x$	$\frac{sin2x}{x}$
-0.1	a.	0.1	e.
-0.01	b.	0.01	f.
-0.001	c.	0.001	g.
-0.0001	d.	0.0001	h.

Answer:: a. 1.98669331
b. 1.99986667
c. 1.99999867
d. 1.99999999
e. 1.98669331
f. 1.99986667
g. 1.99999867
h. 1.99999999
It appears that: $\displaystyle \lim_{x \to 0}\frac{sin2x}{x}=2$

36) [T] $\displaystyle \lim_{x \to 0}\frac{\sin(3x)}{x} ±0.1, ±0.01, ±0.001, ±0.0001$

$x$	$\frac{sin3x}{x}$	$x$	$\frac{sin3x}{x}$
-0.1	a.	0.1	e.
-0.01	b.	0.01	f.
-0.001	c.	0.001	g.
-0.0001	d.	0.0001	h.

37) Use the preceding two exercises to conjecture (guess) the value of the following limit: $\displaystyle \lim_{x \to 0}\frac{\sin(ax)}{x}$ for a, a positive real value.

Answer:: It appears that: $\displaystyle \lim_{x \to 0}\frac{sinax}{x}=a$

[T] In the following exercises, set up a table of values to find the indicated limit. Round to eight digits.

38) $\displaystyle \lim_{x \to 2}\frac{x^2−4}{x^2+x−6}$

$x$	$\frac{x^2−4}{x^2+x−6}$	$x$	$\frac{x^2−4}{x^2+x−6}$
1.9	a.	2.1	e.
1.99	b.	2.01	f.
1.999	c.	2.001	g.
1.9999	d.	2.0001	h.

39) $\displaystyle \lim_{x \to 1}(1−2x)$

$x$	$1−2x$	$x$	$1−2x$
0.9	a.	1.1	e.
0.99	b.	1.01	f.
0.999	c.	1.001	g.
0.9999	d.	1.0001	h.

Answer:

a. −0.80000000
b. −0.98000000
c. −0.99800000
d. −0.99980000
e. −1.2000000
f. −1.0200000
g. −1.0020000
h. −1.0002000;

It appears that: $\displaystyle \lim_{x \to 1}(1−2x)=−1$

40) $\displaystyle \lim_{x \to 0}\frac{5}{1−e^{1/x}}$

$x$	$\frac{5}{1−e^{1/x}}$	$x$	$\frac{5}{1−e^{1/x}}$
-0.1	a.	0.1	e.
-0.01	b.	0.01	f.
-0.001	c.	0.001	g.
-0.0001	d.	0.0001	h.

41) $\displaystyle \lim_{z \to 0}\frac{z−1}{z^2(z+3)}$

$z$	$\frac{z−1}{z^2(z+3)}$	$z$	$\frac{z−1}{z^2(z+3)}$
-0.1	a.	0.1	e.
-0.01	b.	0.01	f.
-0.001	c.	0.001	g.
-0.0001	d.	0.0001	h.

Answer:

a. −37.931934
b. −3377.9264
c. −333,777.93
d. −33,337,778
e. −29.032258
f. −3289.0365
g. −332,889.04
h. −33,328,889

It appears that: $\lim_{x \to 0}\frac{z−1}{z^2(z+3)}=−∞$

42) $\displaystyle \lim_{t \to 0^+}\frac{\cos(t)}{t}$

\(t)	$\frac{cost}{t}$
0.1	a.
0.01	b.
0.001	c.
0.0001	d.

43) $\displaystyle \lim_{x \to 2}\frac{1−\frac{2}{x}}{x^2−4}$

$x$	$\frac{1−\frac{2}{x}}{x^2−4}$	$x$	$\frac{1−\frac{2}{x}}{x^2−4}$
1.9	a.	2.1	e.
1.99	b.	2.01	f.
1.999	c.	2.001	g.
1.9999	d.	2.0001	h.

Answer:

a. 0.13495277
b. 0.12594300
c. 0.12509381
d. 0.12500938
e. 0.11614402
f. 0.12406794
g. 0.12490631
h. 0.12499063

It appears that: $\displaystyle \lim_{x \to 2}\frac{1−\frac{2}{x}}{x^2−4}=0.1250=\frac{1}{8}$

[T] In the following exercises, set up a table of values and round to eight significant digits. Based on the table of values, make a guess about what the limit is. Then, use a calculator to graph the function and determine the limit. Was the conjecture correct? If not, why does the method of tables fail?

44) $\displaystyle \lim_{θ \to 0}sin(\frac{π}{θ})$

$θ$	$sin(\frac{π}{θ})$	$θ$	$sin(\frac{π}{θ})$
-0.1	a.	0.1	e.
-0.01	b.	0.01	f.
-0.001	c.	0.001	g.
-0.0001	d.	0.0001	h.

45) $\displaystyle \lim_{α \to 0^+} \frac{1}{α}\cos(\frac{π}{α})$

$a$	$\frac{1}{α}cos(\frac{π}{α})$
0.1	a.
0.01	b.
0.001	c.
0.0001	d.

Answer:

a. −10.00000; b. −100.00000; c. −1000.0000; d. −10,000.000

It appears from the table: $\displaystyle \lim_{α→0^+}\frac{1}{α}\cos(\frac{π}{α})=-∞$
actual answer (see graph): DNE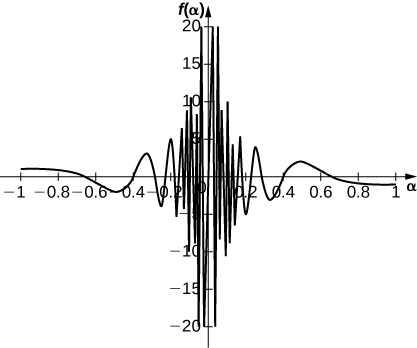

Estimating limits from GRAPHS

Note: Exercises #46 - #49 moved to section 2.4 Exercises

In the following exercises, use the following graph of the function $y=f(x)$ to find the values, if possible. Estimate when necessary.

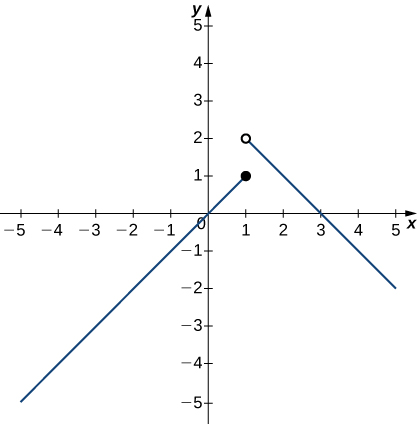
50) $\displaystyle \lim_{x→1^−}f(x)$

51) $\displaystyle \lim_{x→1^+}f(x)$

Answer:: 2

52) $\displaystyle \lim_{x→1}f(x)$

53) $\displaystyle \lim_{x→2}f(x)$

Answer:: 1

54) $f(1)$

In the following exercises, use the graph of the function $y=f(x)$ shown here to find the values, if possible. Estimate when necessary.

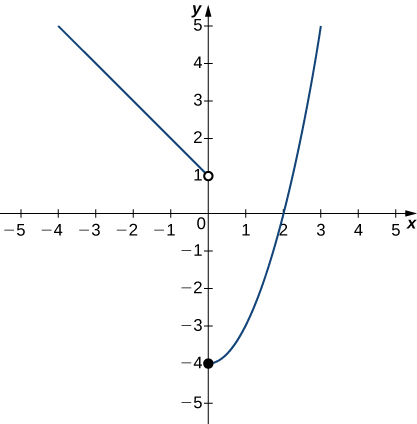
55) $\displaystyle \lim_{x→0^−}f(x)$

Answer:: 1

56) $\displaystyle \lim_{x→0^+}f(x)$

57) $\displaystyle \lim_{x→0}f(x)$

Answer:: DNE

58) $\displaystyle \lim_{x→2}f(x)$

In the following exercises, use the graph of the function $y=f(x)$ shown here to find the values, if possible. Estimate when necessary.

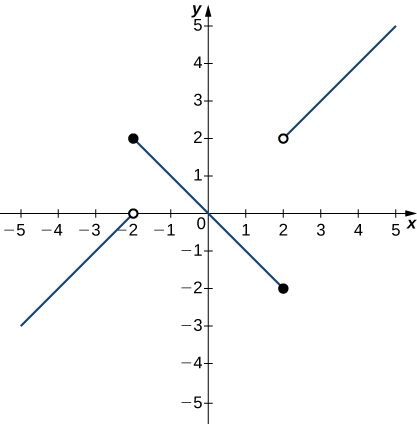
59) $\displaystyle \lim_{x→−2^−}f(x)$

Answer:: 0

60) $\displaystyle \lim_{x→−2^+}f(x)$

61) $\displaystyle \lim_{x→−2}f(x)$

Answer:: DNE

62) $\displaystyle \lim_{x→2^−}f(x)$

63) $\displaystyle \lim_{x→2^+}f(x)$

Answer:: 2

64) $\displaystyle \lim_{x→2}f(x)$

In the following exercises, use the graph of the function $y=g(x)$ shown here to find the values, if possible. Estimate when necessary.

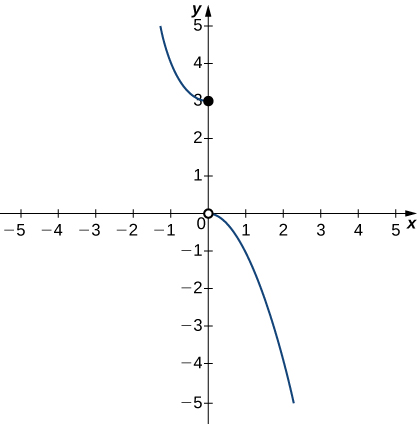
65) $\displaystyle \lim_{x→0^−}g(x)$

Answer:: 3

66) $\displaystyle \lim_{x→0^+}g(x)$

67) $\displaystyle \lim_{x→0}g(x)$

Answer:: DNE

In the following exercises, use the graph of the function $y=h(x)$ shown here to find the values, if possible. Estimate when necessary.

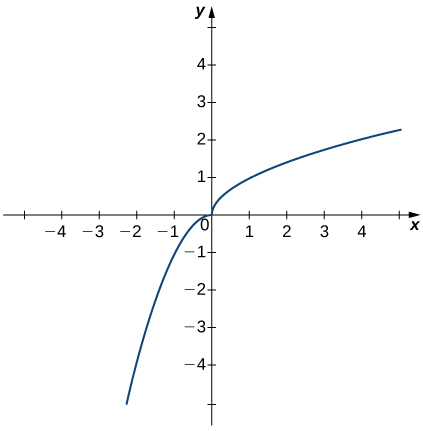
68) $\displaystyle \lim_{x→0^−}h(x)$

69) $\displaystyle \lim_{x→0^+}h(x)$

Answer:: 0

70) $\displaystyle \lim_{x→0}h(x)$

In the following exercises, use the graph of the function $y=f(x)$ shown here to find the values, if possible. Estimate when necessary.

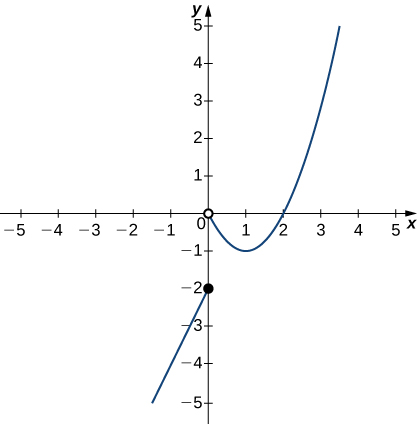
71) $\displaystyle \lim_{x→0^−}f(x)$

Answer:: −2

72) $\displaystyle \lim_{x→0^+}f(x)$

73) $\displaystyle \lim_{x→0}f(x)$

Answer:: DNE

74) $\displaystyle \lim_{x→1}f(x)$

75) $\displaystyle \lim_{x→2}f(x)$

Answer:: 0

In the following exercises, sketch the graph of a function with the given properties.

76) $\displaystyle \lim_{x→2}f(x)=1, \displaystyle \lim_{x→4^−}f(x)=3, \displaystyle \lim_{x→4^+}f(x)=6,x=4$ is not defined.

77) $\displaystyle \lim_{x→−∞}f(x)=0, \displaystyle \lim_{x→−1^−}f(x)=−∞, \displaystyle \lim_{x→−1^+}f(x)=∞, \displaystyle \lim_{x→0}f(x)=f(0), f(0)=1, \displaystyle \lim_{x→∞}f(x)=−∞$

Answer:

Answer may vary

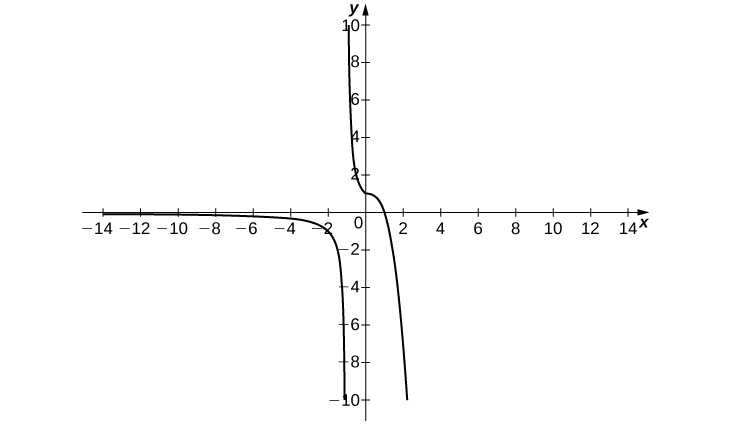
78) $\displaystyle \lim_{x→−∞}f(x)=2, \displaystyle \lim_{x→3^−}f(x)=−∞, \displaystyle \lim_{x→3^+}f(x)=∞, \displaystyle \lim_{x→∞}f(x)=2,f(0)=\frac{−1}{3}$

79) $ \displaystyle \lim_{x→−∞}f(x)=2, \displaystyle \lim_{x→−2}f(x)=−∞, \displaystyle \lim_{x→∞} f(x)=2,f(0)=0$

Answer:

Answer may vary

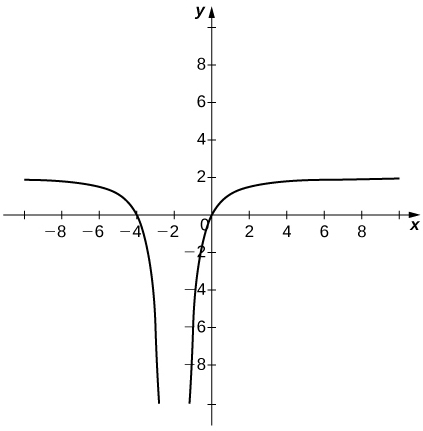
80)$\displaystyle \lim_{x→−∞}f(x)=0, \displaystyle \lim_{x→−1^−}f(x)=∞, \displaystyle \lim_{x→−1^+}f(x)=−∞, f(0)=−1, \displaystyle \lim_{x→1^−}f(x)=−∞, \displaystyle \lim_{x→1^+}f(x)=∞, \displaystyle \lim_{x→∞}f(x)=0$

81) Shock waves arise in many physical applications, ranging from supernovas to detonation waves. A graph of the density of a shock wave with respect to distance, x, is shown here. We are mainly interested in the location of the front of the shock, labeled xSF in the diagram.

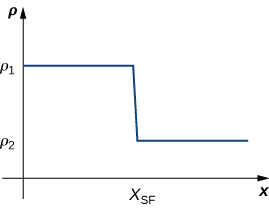
a. Evaluate $\displaystyle \lim_{x→x_{SF}^+}ρ(x)$.

b. Evaluate $\displaystyle \lim_{x→x_{SF}^−}ρ(x)$.

c. Evaluate $\displaystyle \lim_{x→x_{SF}}ρ(x)$. Explain the physical meanings behind your answers.

Answer:: a. $ρ_2$
b. $ρ_1$
c. DNE unless $ρ_1=ρ_2$. As you approach xSF from the right, you are in the high-density area of the shock. When you approach from the left, you have not experienced the “shock” yet and are at a lower density.

82) A track coach uses a camera with a fast shutter to estimate the position of a runner with respect to time. A table of the values of position of the athlete versus time is given here, where x is the position in meters of the runner and t is time in seconds. What is $\displaystyle \lim_{t→2}x(t)$? What does it mean physically?

$t(sec)$	$x(m)$
1.75	4.5
1.95	6.1
1.99	6.42
2.01	6.58
2.05	6.9
2.25	8.5