4.5: Optimization Problems
- Page ID
- 13659
One common application of calculus is calculating the minimum or maximum value of a function. For example, companies often want to minimize production costs or maximize revenue. In manufacturing, it is often desirable to minimize the amount of material used to package a product with a certain volume. In this section, we show how to set up these types of minimization and maximization problems and solve them by using the tools developed in this chapter.
The basic idea of the optimization problems that follow is the same. We have a particular quantity that we are interested in maximizing or minimizing. However, we also have some auxiliary condition that needs to be satisfied. For example, in Example \(\PageIndex{1}\), we are interested in maximizing the area of a rectangular garden. Certainly, if we keep making the side lengths of the garden larger, the area will continue to become larger. However, what if we have some restriction on how much fencing we can use for the perimeter? In this case, we cannot make the garden as large as we like. Let’s look at how we can maximize the area of a rectangle subject to some constraint on the perimeter.
Example \(\PageIndex{1}\): Maximizing the Area of a Garden
A rectangular garden is to be constructed using a rock wall as one side of the garden and wire fencing for the other three sides (Figure). Given \(100\) ft of wire fencing, determine the dimensions that would create a garden of maximum area. What is the maximum area?
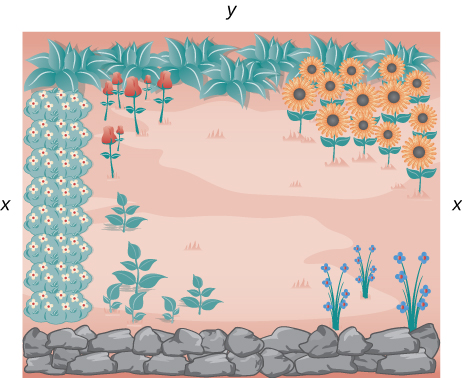
Figure \(\PageIndex{1}\): We want to determine the measurements x and y that will create a garden with a maximum area using 100 ft of fencing.
Solution: Let \(x\) denote the length of the side of the garden perpendicular to the rock wall and \(y\) denote the length of the side parallel to the rock wall. Then the area of the garden is
\(A=x⋅y.\)
We want to find the maximum possible area subject to the constraint that the total fencing is \(100ft.\) From Figure, the total amount of fencing used will be \(2x+y.\) Therefore, the constraint equation is
\(2x+y=100.\)
Solving this equation for \(y\), we have \(y=100−2x.\) Thus, we can write the area as
\(A(x)=x⋅(100−2x)=100x−2x^2.\)
Before trying to maximize the area function \(A(x)=100x−2x^2,\) we need to determine the domain under consideration. To construct a rectangular garden, we certainly need the lengths of both sides to be positive. Therefore, we need \(x>0\) and \(y>0\). Since \(y=100−2x\), if \(y>0\), then \(x<50\). Therefore, we are trying to determine the maximum value of A(x) for x over the open interval \((0,50)\).
Maximize \(A(x)=100x−2x^2\) over the interval \((0,50)\).
Differentiating the function \(A(x)\), we obtain
\(A′(x)=100−4x.\)
Solving for x, we get the only critical point is \(x=25\)
We use the same process to look for a maximum or a minimum. At this point, we use the Second Derivative Test (SDT) determine if this critical point corresponds to a minimum or a maximum.
\(A′′(x)=−4,\) thus \(A′′(25)=−4\). Since the second derivative at \(x=25\) is negative, we conclude that the maximum area must occur when \(x=25\). Then we have \(y=100−2x=100−2(25)=50.\) To maximize the area of the garden, let \(x=25\) ft and \(y=50\) ft. The area of this garden is \(1250\) \(ft^2\).
ANSWER: The maximum area of this garden is \(1250\) \(ft^2\).
See Figure\(\PageIndex{2}\).
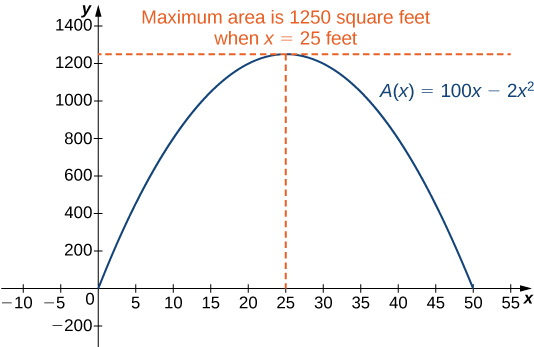
Figure \(\PageIndex{2}\): To maximize the area of the garden, we need to find the maximum value of the function \(A(x)=100x−2x^2\).
![]() Exercise \(\PageIndex{1}\)
Exercise \(\PageIndex{1}\)
Determine the maximum area if we want to make the same rectangular garden as in Figure, but we have \(200\) ft of fencing.
- Hint
-
We need to maximize the function \(A(x)=200x−2x^2\) over the interval \([0,100].\)
- Answer
-
The maximum area is \(5000\) \(ft^2\).
Now let’s look at a general strategy for solving optimization problems similar to Example \(\PageIndex{1}\).
 Steps to Solve Optimization Problems
Steps to Solve Optimization Problems
- Determine which quantity is to be optimized; is it to be maximized or minimized? If applicable, draw a figure and label all variables.
- Write a formula (function) for the quantity to be optimized in terms of the variables. Write constraint equation(s) on the side.
- Write your function from step \(2\) in terms of one variable (use the constraints to relate variables). Identify the domain based on the physical problem to be solved.
- Find the derivative of your function.
- Set the derivative equal to zero & solve to find critical points.
- Test the critical point to see if it yields a maximum or minimum value of the function; use second derivative test (SDT) (or first (FDT)) & also consider endpoints.
- If needed, find the value of the "other" variable.
- If needed, calculate the quantity to optimize.
- State the answer to the question.
Now let’s apply this strategy to maximize the volume of an open-top box given a constraint on the amount of material to be used.
Example \(\PageIndex{2}\): Maximizing the Volume of a Box
An open-top box is to be made from a \(24\) in. by \(36\) in. piece of cardboard by removing a square from each corner of the box and folding up the flaps on each side. What size square should be cut out of each corner to get a box with the maximum volume?
Solution: Step 0: Let x be the side length of the square to be removed from each corner (Figure). Then, the remaining four flaps can be folded up to form an open-top box. Let \(V\) be the volume of the resulting box.
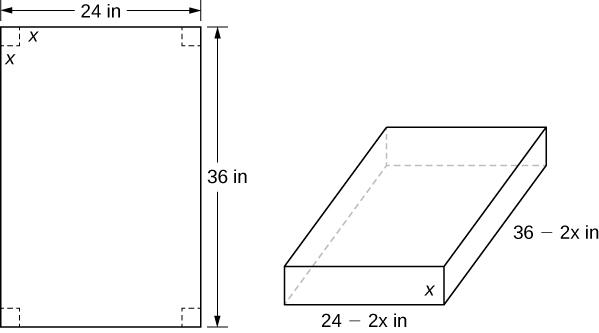
Figure \(\PageIndex{3}\): A square with side length x inches is removed from each corner of the piece of cardboard. The remaining flaps are folded to form an open-top box.
Step 1: We are trying to maximize the volume of a box. Therefore, the problem is to maximize \(V\).
Step 2: The volume of a box is \(V=L⋅W⋅H\), where \(L,W,\)and \(H\) are the length, width, and height, respectively.
Step 3: From Figure, we see that the height of the box is \(x\) inches, the length is \(36−2x\) inches, and the width is \(24−2x\) inches. Therefore, the volume of the box is
\(V(x)=(36−2x)(24−2x)x=4x^3−120x^2+864x\).
To determine the domain of consideration, let’s examine Figure \(\PageIndex{3}\). Certainly, we need \(x>0.\) Furthermore, the side length of the square cannot be greater than or equal to half the length of the shorter side, \(24\) in.; otherwise, one of the flaps would be completely cut off. Therefore, we are trying to determine whether there is a maximum volume of the box for x over the open interval \((0,12).\)
Step 4: The derivative is \(V′(x)=12x^2−240x+864.\)
Step 5: To find the critical points, we need to solve the equation
\(12x^2−240x+864=0.\)
Dividing both sides of this equation by \(12\), the problem simplifies to solving the equation
\(x^2−20x+72=0.\)
Using the quadratic formula, we find that the critical points are
\(x=\dfrac{20±\sqrt{(−20)^2−4(1)(72)}}{2}=\dfrac{20±\sqrt{112}}{2}=\dfrac{20±4\sqrt{7}}{2}=10±2\sqrt{7}\).
Since \(10+2\sqrt{7}\) is not in the domain of consideration, the only critical point we need to consider is \(10−2\sqrt{7}\).
Step 6: SDT: The second derivative is \(V′′(x)=24x−240.\) \(V′′(10-2\sqrt{7})=24(10-2\sqrt{7})−240 =−48\sqrt{7}.\) Since \(V′′(x)<0,\) we have found a maximum.
Step 7: there is no other variable.
Step 8: Therefore, the volume is maximized if we let \(x=10−2\sqrt{7}\) in. The maximum volume is \(V(10−2\sqrt{7})=640+448\sqrt{7}≈1825\) \(in.^3\) as shown in the following graph.
Step 9: ANSWER: Squares with sides of \(10−2\sqrt{7}\) in. should be cut out of the corners to obtain the maximum volume.
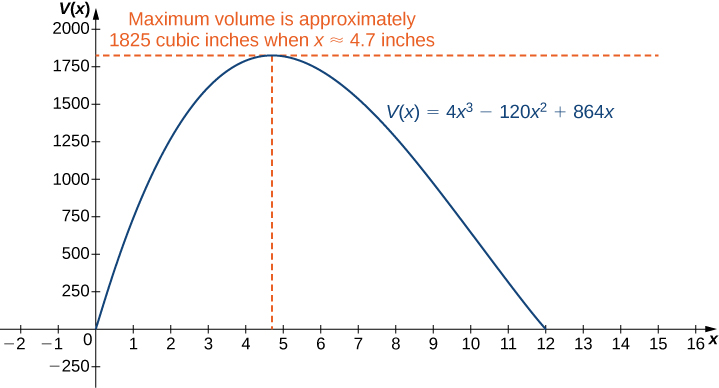
Figure \(\PageIndex{4}\): Maximizing the volume of the box leads to finding the maximum value of a cubic polynomial.
Watch a video about optimizing the volume of a box.
![]() Exercise \(\PageIndex{2}\)
Exercise \(\PageIndex{2}\)
Suppose the dimensions of the cardboard in Example are 20 in. by 30 in. Let \(x\) be the side length of each square and write the volume of the open-top box as a function of \(x\). Determine the domain of consideration for \(x\).
- Hint
-
The volume of the box is \(L⋅W⋅H.\)
- Answer
-
\(V(x)=x(20−2x)(30−2x).\) The domain is \((0,10)\).
Example \(\PageIndex{3}\): Minimizing Travel Time
An island is \(2\) mi due north of its closest point along a straight shoreline. A visitor is staying at a cabin on the shore that is \(6\) mi west of that point. The visitor is planning to go from the cabin to the island. Suppose the visitor runs at a rate of \(8\) mph and swims at a rate of \(3\) mph. How far should the visitor run before swimming to minimize the time it takes to reach the island?
Solution
Step 0: Let \(x\) be the distance running and let \(y\) be the distance swimming (Figure). Let \(T\) be the time it takes to get from the cabin to the island.
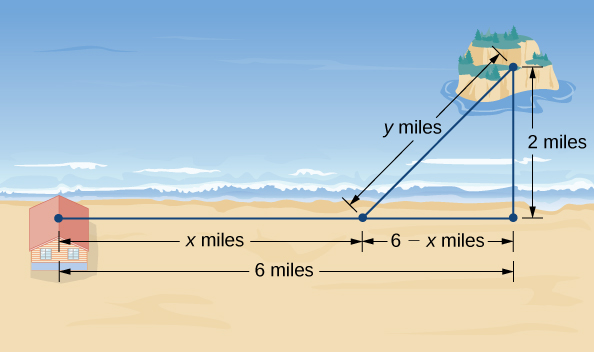
Figure \(\PageIndex{5}\): How can we choose \(x\) and y to minimize the travel time from the cabin to the island?
Step 1: The problem is to minimize \(T\), the travel time.
Step 2: To find the time spent traveling from the cabin to the island, add the time spent running and the time spent swimming. Since Distance = Rate × Time \((D=R×T),\) the time spent running is
\(T_{running}=\dfrac{D_{running}}{R_{running}}=\dfrac{x}{8}\),
and the time spent swimming is
\(T_{swimming}=\dfrac{D_{swimming}}{R_{swimming}}=\dfrac{y}{3}\).
Therefore, the total time spent traveling is
\(T=\dfrac{x}{8}+\dfrac{y}{3}\).
Step 3: From Figure, the line segment of \(y\) miles forms the hypotenuse of a right triangle with legs of length \(2\) mi and \(6−x\) mi. Therefore, by the Pythagorean theorem, \(2^2+(6−x)^2=y^2\), and we obtain \(y=\sqrt{(6−x)^2+4}\). Thus, the total time spent traveling is given by the function
\(T(x)=\dfrac{x}{8}+\dfrac{\sqrt{(6−x)^2+4}}{3}\).
From Figure, we see that \(0≤x≤6\). Therefore, \([0,6]\) is the domain of consideration.
Step 4: The derivative is
\[T′(x)=\dfrac{1}{8}−\dfrac{1}{2}\dfrac{[(6−x)^2+4]^{−1/2}}{3}⋅2(6−x)=\dfrac{1}{8}−\dfrac{(6−x)}{3\sqrt{(6−x)^2+4}}\]
Step 5: If \(T′(x)=0,\) then
\[\dfrac{1}{8}=\dfrac{6−x}{3\sqrt{(6−x)^2+4}}\]
Therefore,
\[3\sqrt{(6−x)^2+4}=8(6−x).\]
Squaring both sides of this equation, we see that if \(x\) satisfies this equation, then \(x\) must satisfy
\[9[(6−x)^2+4]=64(6−x)^2,\]
which implies
\[55(6−x)^2=36.\]
We conclude that if \(x\) is a critical point, then \(x\) satisfies
\[(x−6)^2=\dfrac{36}{55}.\]
Therefore, the possibilities for critical points are
\[x=6±\dfrac{6}{\sqrt{55}}.\]
Since \(x=6+6/\sqrt{55}\) is not in the domain, it is not a possibility for a critical point. On the other hand, \(x=6−6/\sqrt{55}\) is in the domain. Since we squared both sides of an equation to arrive at the possible critical points, it remains to verify that \(x=6−6/\sqrt{55}\) satisfies does satisfy the equation. \(x=6−6/\sqrt{55}\) does satisfy that equation, we conclude that \(x=6−6/\sqrt{55}\) is a critical point, and it is the only one.
Step 6: Rather than use the Second Derivative Test (which does not look quick to use) we can use the fact that \(T(x)\) is a continuous function over a closed, bounded interval, and thus must have a maximum and a minimum. We just need to check the values of \(T(x)\) at the endpoints \(x=0\) and \(x=6\), and compare them with the value of \(T(x)\) at the critical point \(x=6−6/\sqrt{55}\). We find that \(T(0)≈2.108h\) and \(T(6)≈1.417\) h, whereas \(T(6−6/\sqrt{55})≈1.368\) h. Therefore, we conclude that \(T\) has a local minimum at \(x≈5.19\) mi.
Step 7 & Step 8: not asked for in this problem.
Step 9: ANSWER: The visitor should run \(6−6/\sqrt{55}\) mi (about \(5.19\) mi) before swimming in order to minimize the time traveled.
![]() Exercise \(\PageIndex{3}\)
Exercise \(\PageIndex{3}\)
Suppose the island is \(1\) mi from shore, and the distance from the cabin to the point on the shore closest to the island is \(15\) mi. Suppose a visitor swims at the rate of \(2.5\) mph and runs at a rate of \(6\) mph. Let \(x\) denote the distance the visitor will run before swimming, and find a function for the time it takes the visitor to get from the cabin to the island.
- Hint
-
The time \(T=T_{running}+T_{swimming}.\)
- Answer
-
\[T(x)=\dfrac{x}{6}+\dfrac{\sqrt{(15−x)^2+1}}{2.5}\]
In business, companies are interested in maximizing revenue. In the following example, we consider a scenario in which a company has collected data on how many cars it is able to lease, depending on the price it charges its customers to rent a car. Let’s use these data to determine the price the company should charge to maximize the amount of money it brings in.
Example \(\PageIndex{4}\): Maximizing Revenue
Owners of a car rental company have determined that if they charge customers \(p\) dollars per day to rent a car, where \(50≤p≤200\), the number of cars \(n\) they rent per day can be modeled by the linear function \(n(p)=1000−5p\). If they charge \($50\) per day or less, they will rent all their cars. If they charge \($200\) per day or more, they will not rent any cars. Assuming the owners plan to charge customers between \($50\) per day and \($200\) per day to rent a car, how much should they charge to maximize their revenue?
Solution
Step 0: Let \(p\) be the price charged per car per day and let n be the number of cars rented per day. Let \(R\) be the revenue per day.
Step 1: The problem is to maximize \(R.\)
Step 2: The revenue (per day) is equal to the number of cars rented per day times the price charged per car per day—that is, \(R=n×p.\)
Step 3: Since the number of cars rented per day is modeled by the linear function \(n(p)=1000−5p,\) the revenue \(R\) can be represented by the function
\(R(p)=n×p=(1000−5p)p=−5p^2+1000p.\)
Since the owners plan to charge between \($50\) per car per day and \($200\) per car per day, the problem is to find the maximum revenue \(R(p)\) for \(p\) in the closed interval \([50,200]\).
Step 4: The derivative is \(R′(p)=−10p+1000.\)
Step 5: Set the derivative equal to zero \(−10p+1000=0\)
Therefore, the critical point is \(p=100\)
Step 6: SDT: \(R′′(p)=−10,\) so \(R′′(100)=−10,\) \(R′′(x)<0,\) we have found a maximum.
When \(p=100, R(100)=$50,000.\)
Checking the endpoints: when \(p=50, R(p)=$37,500\) & when \(p=200, R(p)=$0\). Therefore, the absolute maximum occurs at \(p=$100\). T
Step 7 & Step 8: not asked for in this problem.
Step 9: ANSWER: The car rental company should charge \($100\) per car per day to maximize revenue as shown in the following figure.
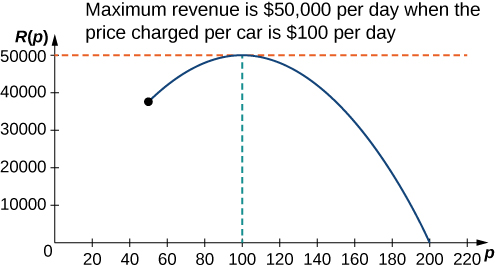
Figure \(\PageIndex{6}\): To maximize revenue, a car rental company has to balance the price of a rental against the number of cars people will rent at that price.
Exercise \(\PageIndex{4}\)
A car rental company charges its customers \(p\) dollars per day, where \(60≤p≤150\). It has found that the number of cars rented per day can be modeled by the linear function \(n(p)=750−5p.\) How much should the company charge each customer to maximize revenue?
- Hint
-
\(R(p)=n×p,\) where \(n\) is the number of cars rented and \(p\) is the price charged per car.
- Answer
-
The company should charge \($75\) per car per day.
Example \(\PageIndex{5}\): Maximizing the Area of an Inscribed Rectangle
A rectangle is to be inscribed in the ellipse given by this equation:
\[\dfrac{x^2}{4}+y^2=1.\]
What should the dimensions of the rectangle be to maximize its area? What is the maximum area?
Solution:
Step 0: For a rectangle to be inscribed in the ellipse, the sides of the rectangle must be parallel to the axes. Let \(L\) be the length of the rectangle and \(W\) be its width. Let \(A\) be the area of the rectangle.
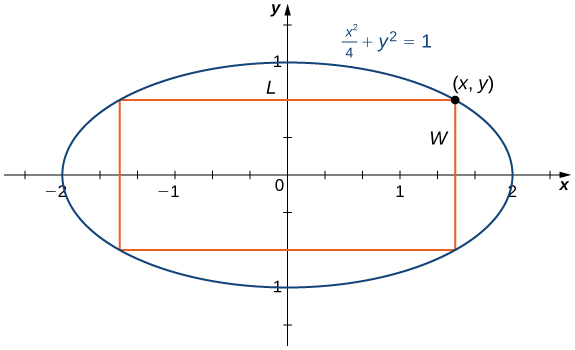
Figure \(\PageIndex{7}\): We want to maximize the area of a rectangle inscribed in an ellipse.
Step 1: The problem is to maximize the area of the rectangle, \(A\).
Step 2: The area of the rectangle is \(A=LW.\)
Step 3: Let \((x,y)\) be the corner of the rectangle that lies in the first quadrant, as shown in Figure. We can write length \(L=2x\) and width \(W=2y\). Since \(\dfrac{x^2}{4+y^2=1}\) and \(y>0\), we have \(y=\sqrt{\dfrac{1−x^2}{4}}\). Therefore, the area is
\(A=LW=(2x)(2y)=4x\sqrt{\dfrac{1−x^2}{4}}=2x\sqrt{4−x^2}\)
From Figure, we see that to inscribe a rectangle in the ellipse, the \(x\)-coordinate of the corner in the first quadrant must satisfy \(0<x<2\). Therefore, the problem reduces to looking for the maximum value of \(A(x)\) over the open interval \((0,2)\).
Step 4: Taking the derivative of \(A(x)\), we obtain
\(A'(x)=2\sqrt{4−x^2}+2x⋅\dfrac{1}{2\sqrt{4−x^2}}(−2x)\)
\(=2\sqrt{4−x^2}−\dfrac{2x^2}{\sqrt{4−x^2}}\)
\(=\dfrac{8−4x^2}{\sqrt{4−x^2}}\).
Step 5: Setting the derivative equal to zero
\(\dfrac{8−4x^2}{\sqrt{4−x^2}}=0\),
then \(x\) must satisfy
\(8−4x^2=0.\)
Therefore, \(x^2=2.\) Thus, \(x=±\sqrt{2}\) are the possible solutions of our equation. Since we are considering \(x\) over the interval \([0,2]\), \(x=\sqrt{2}\) is a possibility for a critical point, but \(x=−\sqrt{2}\) is not. Therefore, we check whether \(\sqrt{2}\) is a solution of our equation. Since \(x=\sqrt{2}\) is a solution of our equation, we conclude that \(\sqrt{2}\) is the only critical point of \(A(x)\) in the interval \((0,2)\).
Step 6: The First Derivative Test might be easier than finding the second derivative. Staying within the domain we get:
\(A'\) + -
____|_______*_________|
0.1 \(\sqrt{2}\) 1.9 indicating we have a maximum at \(x=\sqrt{2}.\)
If you use the SDT, you get \(A''(x)=\dfrac{4x(x^2-6)}{(4−x^2)^{3/2}}\) and \(A''(\sqrt{2})<0\), therefore a maximum at \(x=\sqrt{2}.\)
\(A(x)\) has an absolute maximum at the critical point \(x=\sqrt{2}\).
Step 7: To determine the dimensions of the rectangle, we need to find the length \(L\) and the width \(W\). If \(x=\sqrt{2}\) then
\[y=\sqrt{1−\dfrac{(\sqrt{2})^2}{4}}=\sqrt{1−\dfrac{1}{2}}=\dfrac{1}{\sqrt{2}}.\]
length \(L=2x\) and width \(W=2y\), so \(L=2\sqrt{2}\) and \(W=\dfrac{2}{\sqrt{2}}=\sqrt{2}\).
Step 8: The area of this rectangle is\( A=LW=(2\sqrt{2})(\sqrt{2})=4.\)
Step 9: ANSWER: (a) The dimensions of the rectangle to maximize the area are \(L=2\sqrt{2}\) and \(W=\sqrt{2}\).
(b) The maximum area of this rectangle is \(4.\)
![]() Exercise \(\PageIndex{5}\)
Exercise \(\PageIndex{5}\)
Modify the area function \(A\) if the rectangle is to be inscribed in the unit circle \(x^2+y^2=1\). What is the domain of consideration?
- Hint
-
If \((x,y)\) is the vertex of the square that lies in the first quadrant, then the area of the square is \(A=(2x)(2y)=4xy.\)
- Answer
-
\(A(x)=4x\sqrt{1−x^2}.\) The domain of consideration is \((0,1)\).
In the previous examples, we considered functions on closed, bounded domains. Consequently, by the extreme value theorem, we were guaranteed that the functions had absolute extrema. Let’s now consider functions for which the domain is neither closed nor bounded.
Many functions still have at least one absolute extrema, even if the domain is not closed or the domain is unbounded. For example, the function \(f(x)=x^2+4\) over \((−∞,∞)\) has an absolute minimum of \(4\) at \(x=0\). Therefore, we can still consider functions over unbounded domains or open intervals and determine whether they have any absolute extrema. In the next example, we try to minimize a function over an unbounded domain. We will see that, although the domain of consideration is \((0,∞),\) the function has an absolute minimum.
In the following example, we look at constructing a box of least surface area with a prescribed volume. It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the smallest surface area. Consequently, we consider the modified problem of determining which open-topped box with a specified volume has the smallest surface area.
Example \(\PageIndex{6}\): Minimizing Surface Area
A rectangular box with a square base, an open top, and a volume of \(216 in.^3\) is to be constructed. What should the dimensions of the box be to minimize the surface area of the box? What is the minimum surface area?
Solution
Step 0: Draw a rectangular box and introduce the variable \(x\) to represent the length of each side of the square base; let \(y\) represent the height of the box. Let \(S\) denote the surface area of the open-top box.
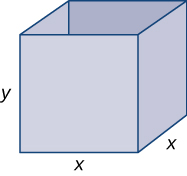
Figure \(\PageIndex{8}\): We want to minimize the surface area of a square-based box with a given volume.
Step 1: We need to minimize the surface area, \(S\).
Step 2: Since the box has an open top, we need only determine the area of the four vertical sides and the base. The area of each of the four vertical sides is \(x⋅y.\) The area of the base is \(x^2\). Therefore, the surface area of the box is
\(S=4xy+x^2\).
Step 3: Since the volume of this box is \(x^2y\) and the volume is given as \(216in.^3\), the constraint equation is
\(x^2y=216\).
Solving the constraint equation for \(y\), we have \(y=\dfrac{216}{x^2}\). Therefore, we can write the surface area as a function of \(x\) only:
\[S(x)=4x(\dfrac{216}{x^2})+x^2.\]
Therefore, \(S(x)=\dfrac{864}{x}+x^2\).
Since we are requiring that \(x^2y=216\), we cannot have \(x=0\). Therefore, we need \(x>0\). On the other hand, \(x\) is allowed to have any positive value. Note that as \(x\) becomes large, the height of the box \(y\) becomes correspondingly small so that \(x^2y=216\). Similarly, as \(x\) becomes small, the height of the box becomes correspondingly large. We conclude that the domain is the open, unbounded interval \((0,∞)\).
Step 4: The derivative is \[S′(x)=−\dfrac{864}{x^2}+2x.\]
Step 5: setting the derivative equal to zero, \(2x=\dfrac{864}{x^2}\). Solving this equation for \(x\), we obtain \(x^3=432\), so \(x=\sqrt[3]{432}=6\sqrt[3]{2}.\)
Step 6: The second derivative is \[S′′(x)=\dfrac{1728}{x^3}+2.\]
\(S′′(6\sqrt[3]{2})>0\) so we have a minimum at \(x=6\sqrt[3]{2}.\)
Since this is the only critical point of \(S\), the absolute minimum must occur at \(x=6\sqrt[3]{2}\)
Step 7: When \(x=6\sqrt[3]{2}\), \(y=\dfrac{216}{(6\sqrt[3]{2})^2}=3\sqrt[3]{2}\).
Step 8:
With these dimensions, the surface area is
\[S(6\sqrt[3]{2})=\dfrac{864}{6\sqrt[3]{2}}+(6\sqrt[3]{2})^2=108\sqrt[3]{4}\]
Step 9: ANSWER: (a) The dimensions for the minimum surface area are \(6\sqrt[3]{2}\) in. for the length & width of the base and \(3\sqrt[3]{2}\) in. for the height.
(b) The minimum surface area \(108\sqrt[3]{4}\) \(in.^2\)
(see Figure \(\PageIndex{9}\)).
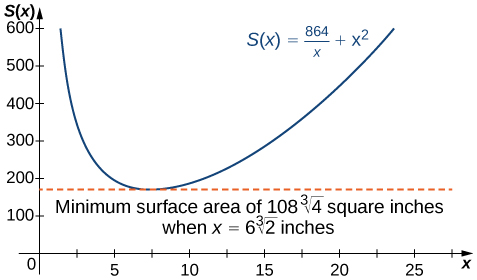
Figure \(\PageIndex{9}\): We can use a graph to determine the dimensions of a box of given the volume and the minimum surface area.
![]() Exercise \(\PageIndex{6}\)
Exercise \(\PageIndex{6}\)
Consider the same open-top box, which is to have volume \(216\) \(in.^3\). Suppose the cost of the material for the base is \(20¢/in.^2\) and the cost of the material for the sides is \(30¢/in.^2\) and we are trying to minimize the cost of this box. Write the cost as a function of the side lengths of the base. (Let \(x\) be the side length of the base and \(y\) be the height of the box.)
- Hint
-
If the cost of one of the sides is \(30¢/in.^2,\) the cost of that side is \(0.30xy.\)
- Answer
-
\(c(x)=\dfrac{259.2}{x}+0.2x^2\) dollars
Key Concepts
- To solve an optimization problem, begin by drawing a picture and introducing variables.
- Find an equation relating the variables.
- Find a function of one variable to describe the quantity that is to be minimized or maximized.
- Look for critical points to locate local extrema.
Glossary
- optimization problems
- problems that are solved by finding the maximum or minimum value of a function
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


