7.4E: Exercises for Integration by Partial Fractions

Use partial fraction decomposition (or a simpler technique) to express the rational function as a sum or difference of two or more simpler rational expressions.

1) $\dfrac{1}{(x−3)(x−2)}$

2) $\dfrac{x^2+1}{x(x+1)(x+2)}$

Answer

$\dfrac{x^2+1}{x(x+1)(x+2)} \quad = \quad −\dfrac{2}{x+1}+\dfrac{5}{2(x+2)}+\dfrac{1}{2x}$

3) $\dfrac{1}{x^3−x}$

4) $\dfrac{3x+1}{x^2}$

Answer

$\dfrac{3x+1}{x^2} \quad = \quad \dfrac{1}{x^2}+\dfrac{3}{x}$

5) $\dfrac{3x^2}{x^2+1}$ (Hint: Use long division first.)

6) $\dfrac{2x^4}{x^2−2x}$

Answer

$\dfrac{2x^4}{x^2−2x} \quad = \quad 2x^2+4x+8+\dfrac{16}{x−2}$

7) $\dfrac{1}{(x−1)(x^2+1)}$

8) $\dfrac{1}{x^2(x−1)}$

Answer

$\dfrac{1}{x^2(x−1)} \quad = \quad −\dfrac{1}{x^2}−\dfrac{1}{x}+\dfrac{1}{x−1}$

9) $\dfrac{x}{x^2−4}$

10) $\dfrac{1}{x(x−1)(x−2)(x−3)}$

Answer

$\dfrac{1}{x(x−1)(x−2)(x−3)} \quad = \quad −\dfrac{1}{2(x−2)}+\dfrac{1}{2(x−1)}−\dfrac{1}{6x}+\dfrac{1}{6(x−3)}$

11) $\dfrac{1}{x^4−1}=\dfrac{1}{(x+1)(x−1)(x^2+1)}$

12) $\dfrac{3x^2}{x^3−1}=\dfrac{3x^2}{(x−1)(x^2+x+1)}$

Answer

$\dfrac{3x^2}{x^3−1} \quad = \quad \dfrac{1}{x−1}+\dfrac{2x+1}{x^2+x+1}$

13) $\dfrac{2x}{(x+2)^2}$

14) $\dfrac{3x^4+x^3+20x^2+3x+31}{(x+1)(x^2+4)^2}$

Answer

$\dfrac{3x^4+x^3+20x^2+3x+31}{(x+1)(x^2+4)^2} \quad = \quad \dfrac{2}{x+1}+\dfrac{x}{x^2+4}−\dfrac{1}{(x^2+4)^2}$

In exercises 15 - 25, use the method of partial fractions to evaluate each of the following integrals.

15) $\displaystyle ∫\frac{dx}{(x−3)(x−2)}$

16) $\displaystyle ∫\frac{3x}{x^2+2x−8}\,dx$

Answer

$\displaystyle ∫\frac{3x}{x^2+2x−8}\,dx \quad = \quad 2\ln|x+4|+\ln|x-2|+C = \ln\left| (x+4)^2(x-2) \right| + C$

17) $\displaystyle ∫\frac{dx}{x^3−x}$

18) $\displaystyle ∫\frac{x}{x^2−4}\,dx$

Answer

Note that you don't need Partial Fractions here. We use a simple $u$-substitution.
$\displaystyle ∫\frac{x}{x^2−4}\,dx \quad = \quad \tfrac{1}{2}\ln|4−x^2|+C$

19) $\displaystyle ∫\frac{dx}{x(x−1)(x−2)(x−3)}$

20) $\displaystyle ∫\frac{2x^2+4x+22}{x^2+2x+10}\,dx$

Answer

Note that since the degree of the numerator is equal to the degree of the denominator, we need to start with long division.
Then note that we will need to use completing the square to continue since we cannot factor the trinomial in the denominator.
$\displaystyle ∫\frac{2x^2+4x+22}{x^2+2x+10}\,dx \quad = \quad 2\left(x+\tfrac{1}{3}\arctan\left(\frac{1+x}{3}\right)\right)+C$

21) $\displaystyle ∫\frac{dx}{x^2−5x+6}$

22) $\displaystyle ∫\frac{2−x}{x^2+x}\,dx$

Answer

$\displaystyle ∫\frac{2−x}{x^2+x}\,dx \quad = \quad 2\ln|x|−3\ln|1+x|+C = \ln\left| \frac{x^2}{(1+x)^3} \right|+C$

23) $\displaystyle ∫\frac{2}{x^2−x−6}\,dx$

24) $\displaystyle ∫\frac{dx}{x^3−2x^2−4x+8}$

Answer

$\displaystyle ∫\frac{dx}{x^3−2x^2−4x+8} \quad = \quad \tfrac{1}{16}\left(−\frac{4}{−2+x}−\ln|−2+x|+\ln|2+x|\right)+C = \tfrac{1}{16}\left(−\frac{4}{−2+x}+\ln\left| \frac{x+2}{x-2} \right|\right)+C$

25) $\displaystyle ∫\frac{dx}{x^4−10x^2+9}$

In exercises 26 - 29, evaluate the integrals with irreducible quadratic factors in the denominators.

26) $\displaystyle ∫\frac{2}{(x−4)(x^2+2x+6)}\,dx$

Answer

$\displaystyle ∫\frac{2}{(x−4)(x^2+2x+6)}\,dx \quad = \quad \tfrac{1}{30}(−2\sqrt{5}\arctan\left[\frac{1+x}{\sqrt{5}}\right]+2\ln|−4+x|−\ln|6+2x+x^2|)+C$

27) $\displaystyle ∫\frac{x^2}{x^3−x^2+4x−4}\,dx$

28) $\displaystyle ∫\frac{x^3+6x^2+3x+6}{x^3+2x^2}\,dx$

Answer

Note that we need to use long division first, since the degree of the numerator is greater than the degree of the denominator.
$\displaystyle ∫\frac{x^3+6x^2+3x+6}{x^3+2x^2}\,dx \quad = \quad −\frac{3}{x}+4\ln|x+2|+x+C$

29) $\displaystyle ∫\frac{x}{(x−1)(x^2+2x+2)^2}\,dx$

In exercises 30 - 32, use the method of partial fractions to evaluate the integrals.

30) $\displaystyle ∫\frac{3x+4}{(x^2+4)(3−x)}\,dx$

Answer

$\displaystyle ∫\frac{3x+4}{(x^2+4)(3−x)}\,dx \quad = \quad −\ln|3−x|+\tfrac{1}{2}\ln|x^2+4|+C$

31) $\displaystyle ∫\frac{2}{(x+2)^2(2−x)}\,dx$

32) $\displaystyle ∫\frac{3x+4}{x^3−2x−4}\,dx$ (Hint: Use the rational root theorem.)

Answer

$\displaystyle ∫\frac{3x+4}{x^3−2x−4}\,dx \quad = \quad \ln|x−2|−\tfrac{1}{2}\ln|x^2+2x+2|+C$

In exercises 33 - 46, use substitution to convert the integrals to integrals of rational functions. Then use partial fractions to evaluate the integrals.

33) $\displaystyle ∫^1_0\frac{e^x}{36−e^{2x}}\,dx$ (Give the exact answer and the decimal equivalent. Round to five decimal places.)

34) $\displaystyle ∫\frac{e^x}{e^{2x}−e^x}\,dx$

Answer

$\displaystyle ∫\frac{e^x}{e^{2x}−e^x}\,dx \quad = \quad −x+\ln|1−e^x|+C$

35) $\displaystyle ∫\frac{\sin x\,dx}{1−\cos^2x}$

36) $\displaystyle ∫\frac{\sin x}{\cos^2 x+\cos x−6}\,dx$

Answer

$\displaystyle ∫\frac{\sin x}{\cos^2 x+\cos x−6}\,dx \quad = \quad \tfrac{1}{5}\ln\left|\frac{\cos x+3}{\cos x−2}\right|+C$

37) $\displaystyle ∫\frac{1−\sqrt{x}}{1+\sqrt{x}}\,dx$

38) $\displaystyle ∫\frac{dt}{(e^t−e^{−t})^2}$

Answer

$\displaystyle ∫\frac{dt}{(e^t−e^{−t})^2} \quad = \quad \frac{1}{2−2e^{2t}}+C$

39) $\displaystyle ∫\frac{1+e^x}{1−e^x}\,dx$

40) $\displaystyle ∫\frac{dx}{1+\sqrt{x+1}}$

Answer

$\displaystyle ∫\frac{dx}{1+\sqrt{x+1}} \quad = \quad 2\sqrt{1+x}−2\ln|1+\sqrt{1+x}|+C$

41) $\displaystyle ∫\frac{dx}{\sqrt{x}+\sqrt[4]{x}}$

42) $\displaystyle ∫\frac{\cos x}{\sin x(1−\sin x)}\,dx$

Answer

$\displaystyle ∫\frac{\cos x}{\sin x(1−\sin x)}\,dx \quad = \quad \ln\left|\frac{\sin x}{1−\sin x}\right|+C$

43) $\displaystyle ∫\frac{e^x}{(e^{2x}−4)^2}\,dx$

44) $\displaystyle ∫_1^2\frac{1}{x^2\sqrt{4−x^2}}\,dx$

Answer

$\displaystyle ∫_1^2\frac{1}{x^2\sqrt{4−x^2}}\,dx \quad = \quad \frac{\sqrt{3}}{4}$

45) $\displaystyle ∫\frac{1}{2+e^{−x}}\,dx$

46) $\displaystyle ∫\frac{1}{1+e^x}\,dx$

Answer

$\displaystyle ∫\frac{1}{1+e^x}\,dx \quad = \quad x−\ln(1+e^x)+C$

In exercises 47 - 48, use the given substitution to convert the integral to an integral of a rational function, then evaluate.

47) $\displaystyle ∫\frac{1}{t−\sqrt[3]{t}}\,dt; \quad t=x^3$

48) $\displaystyle ∫\frac{1}{\sqrt{x}+\sqrt[3]{x}}\,dx; \quad x=u^6$

Answer

$\displaystyle ∫\frac{1}{\sqrt{x}+\sqrt[3]{x}}\,dx \quad = \quad 6x^{1/6}−3x^{1/3}+2\sqrt{x}−6\ln(1+x^{1/6})+C$

49) Graph the curve $y=\dfrac{x}{1+x}$ over the interval $[0,5]$. Then, find the area of the region bounded by the curve, the $x$-axis, and the line $x=4$.

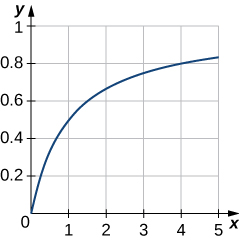
50) Find the volume of the solid generated when the region bounded by $y=\dfrac{1}{\sqrt{x(3−x)}}, \,y=0, \,x=1,$ and $x=2$ is revolved about the $x$-axis.

Answer

$V = \frac{4}{3}π\text{arctanh}\,\left[\frac{1}{3}\right]=\frac{1}{3}π\ln 4 \, \text{units}^3$

51) The velocity of a particle moving along a line is a function of time given by $v(t)=\dfrac{88t^2}{t^2+1}.$ Find the distance that the particle has traveled after $t=5$ sec.

In exercises 52 - 54, solve the initial-value problem for $x$ as a function of $t$.

52) $(t^2−7t+12)\dfrac{dx}{dt}=1,\quad t>4,\, x(5)=0$

Answer

$x=−\ln|t−3|+\ln|t−4|+\ln 2 = \ln\left| \dfrac{2(t-4)}{t-3}\right|$

53) $(t+5)\dfrac{dx}{dt}=x^2+1, \quad t>−5,\,x(1)=\tan 1$

54) $(2t^3−2t^2+t−1)\dfrac{dx}{dt}=3,\quad x(2)=0$

Answer

$x=\ln|t−1|−\sqrt{2}\arctan(\sqrt{2}t)−\frac{1}{2}\ln(t^2+\frac{1}{2})+\sqrt{2}\arctan(2\sqrt{2})+\frac{1}{2}\ln 4.5$

55) Find the $x$-coordinate of the centroid of the area bounded by $y(x^2−9)=1, \, y=0, \,x=4,$ and $x=5.$ (Round the answer to two decimal places.)

56) Find the volume generated by revolving the area bounded by $y=\dfrac{1}{x^3+7x^2+6x},\, x=1,\, x=7$, and $y=0$ about the $y$-axis.

Answer

$V = \frac{2}{5}π\ln\frac{28}{13} \, \text{units}^3$

57) Find the area bounded by $y=\dfrac{x−12}{x^2−8x−20}, \,y=0, \,x=2,$ and $x=4$. (Round the answer to the nearest hundredth.)

58) Evaluate the integral $\displaystyle ∫\frac{dx}{x^3+1}.$

Answer

$\displaystyle ∫\frac{dx}{x^3+1} \quad = \quad \frac{\arctan[\frac{−1+2x}{\sqrt{3}}]}{\sqrt{3}}+\frac{1}{3}\ln|1+x|−\frac{1}{6}\ln∣1−x+x^2∣+C$

For problems 59 - 62, use the substitutions $\tan(\frac{x}{2})=t$, $dx=\dfrac{2}{1+t^2}\,dt$,  $\sin x=\dfrac{2t}{1+t^2}$, and $\cos x=\dfrac{1−t^2}{1+t^2}$.

59) $\displaystyle ∫\frac{dx}{3−5\sin x}$

60) Find the area under the curve $y=\dfrac{1}{1+\sin x}$ between $x=0$ and $x=π.$ (Assume the dimensions are in inches.)

Answer

2.0 in.²

61) Given $\tan\left(\frac{x}{2}\right)=t,$ derive the formulas $dx=\dfrac{2}{1+t^2}dt, \,\sin x=\dfrac{2t}{1+t^2}$, and $\cos x=\dfrac{1−t^2}{1+t^2}.$

62) Evaluate $\displaystyle ∫\frac{\sqrt[3]{x−8}}{x}\,dx.$

Answer

$\displaystyle ∫\frac{\sqrt[3]{x−8}}{x}\,dx \quad = \quad 3(−8+x)^{1/3}−2\sqrt{3}\arctan\left[\frac{−1+(−8+x)^{1/3}}{\sqrt{3}}\right]−2\ln\left[2+(−8+x)^{1/3}\right]+\ln\left[4−2(−8+x)^{1/3}+(−8+x)^{2/3}\right]+C$