7.7: L'Hôpital's Rule
- Last updated
- Mar 22, 2019
- Save as PDF
- Page ID
- 18492
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Recognize when to apply L’Hôpital’s rule.
- Identify indeterminate forms produced by quotients, products, subtractions, and powers, and apply L’Hôpital’s rule in each case.
- Describe the relative growth rates of functions.
In this section, we examine a powerful tool for evaluating limits. This tool, known as L’Hôpital’s rule, uses derivatives to calculate limits. With this rule, we will be able to evaluate many limits we have not yet been able to determine. Instead of relying on numerical evidence to conjecture that a limit exists, we will be able to show definitively that a limit exists and to determine its exact value.
Applying L’Hôpital’s Rule
L’Hôpital’s rule can be used to evaluate limits involving the quotient of two functions. Consider
limx→af(x)g(x).
If limx→af(x)=L1 and limx→ag(x)=L2≠0, then
limx→af(x)g(x)=L1L2.
However, what happens if limx→af(x)=0 and limx→ag(x)=0? We call this one of the indeterminate forms, of type 00. This is considered an indeterminate form because we cannot determine the exact behavior of f(x)g(x) as x→a without further analysis. We have seen examples of this earlier in the text. For example, consider
limx→2x2−4x−2
and
limx→0sinxx.
For the first of these examples, we can evaluate the limit by factoring the numerator and writing
limx→2x2−4x−2=limx→2(x+2)(x−2)x−2=limx→2(x+2)=2+2=4.
For limx→0sinxx we were able to show, using a geometric argument, that
limx→0sinxx=1.
Here we use a different technique for evaluating limits such as these. Not only does this technique provide an easier way to evaluate these limits, but also, and more importantly, it provides us with a way to evaluate many other limits that we could not calculate previously.
The idea behind L’Hôpital’s rule can be explained using local linear approximations. Consider two differentiable functions f and g such that limx→af(x)=0=limx→ag(x) and such that g′(a)≠0 For x near a,we can write
f(x)≈f(a)+f′(a)(x−a)
and
g(x)≈g(a)+g′(a)(x−a).
Therefore,
f(x)g(x)≈f(a)+f′(a)(x−a)g(a)+g′(a)(x−a).
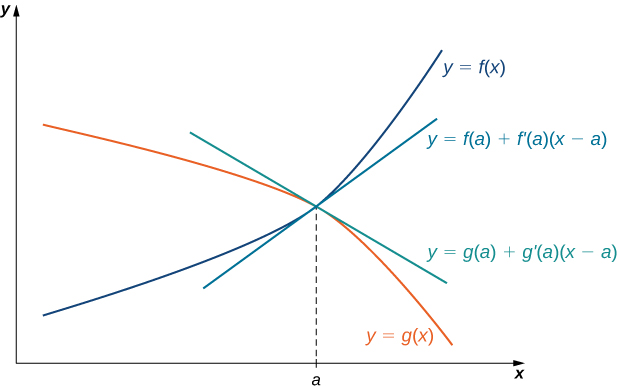
Since f is differentiable at a, then f is continuous at a, and therefore f(a)=limx→af(x)=0. Similarly, g(a)=limx→ag(x)=0. If we also assume that f′ and g′ are continuous at x=a, then f′(a)=limx→af′(x) and g′(a)=limx→ag′(x). Using these ideas, we conclude that
limx→af(x)g(x)=limx→af′(x)(x−a)g′(x)(x−a)=limx→af′(x)g′(x).
Note that the assumption that f′ and g′ are continuous at a and g′(a)≠0 can be loosened. We state L’Hôpital’s rule formally for the indeterminate form 00. Also note that the notation 00 does not mean we are actually dividing zero by zero. Rather, we are using the notation 00 to represent a quotient of limits, each of which is zero.
L’Hôpital’s Rule (0/0 Case)
Suppose f and g are differentiable functions over an open interval containing a, except possibly at a. If limx→af(x)=0 and limx→ag(x)=0, then
limx→af(x)g(x)=limx→af′(x)g′(x),
assuming the limit on the right exists or is ∞ or −∞. This result also holds if we are considering one-sided limits, or if a=∞ or a=−∞.
Proof
We provide a proof of this theorem in the special case when f,g,f′, and g′ are all continuous over an open interval containing a. In that case, since limx→af(x)=0=limx→ag(x) and f and g are continuous at a, it follows that f(a)=0=g(a). Therefore,
limx→af(x)g(x)=limx→af(x)−f(a)g(x)−g(a)Sincef(a)=0=g(a)=limx→af(x)−f(a)x−ag(x)−g(a)x−aMultiply numerator and denominator by1x−a=limx→af(x)−f(a)x−alimx→ag(x)−g(a)x−aThe limit of a quotient is the quotient of the limits.=f′(a)g′(a)By the definition of the derivative=limx→af′(x)limx→ag′(x)By the continuity off′andg′=limx→af′(x)g′(x).The limit of a quotient
Note that L’Hôpital’s rule states we can calculate the limit of a quotient fg by considering the limit of the quotient of the derivatives f′g′. It is important to realize that we are not calculating the derivative of the quotient fg.
□
Example 7.7.1: Applying L’Hôpital’s Rule (0/0 Case)
Evaluate each of the following limits by applying L’Hôpital’s rule.
- limx→01−cosxx
- \displaystyle \lim_{x→1}\dfrac{\sin(πx)}{\ln x}
- \displaystyle \lim_{x→∞}\dfrac{e^{1/x}−1}{1/x}
- \displaystyle \lim_{x→0}\dfrac{\sin x−x}{x^2}
Solution
a. Since the numerator 1−\cos x→0 and the denominator x→0, we can apply L’Hôpital’s rule to evaluate this limit. We have
\lim_{x→0}\dfrac{1−\cos x}{x}=\lim_{x→0}\dfrac{\dfrac{d}{dx}\big(1−\cos x\big)}{\dfrac{d}{dx}\big(x\big)}=\lim_{x→0}\dfrac{\sin x}{1}=\frac{\displaystyle \lim_{x→0}\sin x}{\displaystyle \lim_{x→0}1}=\dfrac{0}{1}=0. \nonumber
b. As x→1, the numerator \sin(πx)→0 and the denominator \ln(x)→0. Therefore, we can apply L’Hôpital’s rule. We obtain
\begin{align*} \lim_{x→1}\dfrac{\sin(πx)}{\ln x}&=\lim_{x→1}\dfrac{π \cos(πx)}{1/x} \\[4pt] &=\lim_{x→1}(πx)\cos(πx) \\[4pt] &=(π⋅1)(−1)=−π. \end{align*} \nonumber
c. As x→∞, the numerator e^{1/x}−1→0 and the denominator \frac{1}{x}→0. Therefore, we can apply L’Hôpital’s rule. We obtain
\lim_{x→∞}\dfrac{e^{1/x}−1}{\dfrac{1}{x}}=\lim_{x→∞}\dfrac{e^{1/x}(\tfrac{−1}{x^2})}{\left(\frac{−1}{x^2}\right)}=\lim_{x→∞}e^{1/x}=e^0=1. \nonumber
d. As x→0, both the numerator and denominator approach zero. Therefore, we can apply L’Hôpital’s rule. We obtain
\lim_{x→0}\dfrac{\sin x−x}{x^2}=\lim_{x→0}\dfrac{\cos x−1}{2x}.\nonumber
Since the numerator and denominator of this new quotient both approach zero as x→0, we apply L’Hôpital’s rule again. In doing so, we see that
\lim_{x→0}\dfrac{\cos x−1}{2x}=\lim_{x→0}\dfrac{−\sin x}{2}=0. \nonumber
Therefore, we conclude that
\lim_{x→0}\dfrac{\sin x−x}{x^2}=0. \nonumber
Exercise \PageIndex{1}
Evaluate \lim\limits_{x→0}\dfrac{x}{\tan x}.
- Hint
-
\dfrac{d}{dx}\big(\tan x\big)=\sec^2x
- Answer
-
1
We can also use L’Hôpital’s rule to evaluate limits of quotients \dfrac{f(x)}{g(x)} in which f(x)→±∞ and g(x)→±∞. Limits of this form are classified as indeterminate forms of type ∞/∞. Again, note that we are not actually dividing ∞ by ∞. Since ∞ is not a real number, that is impossible; rather, ∞/∞ is used to represent a quotient of limits, each of which is ∞ or −∞.
L’Hôpital’s Rule (∞/∞ Case)
Suppose f and g are differentiable functions over an open interval containing a, except possibly at a. Suppose \displaystyle\lim_{x→a}f(x)=∞ (or −∞) and \displaystyle\lim_{x→a}g(x)=∞ (or −∞). Then,
\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)} \nonumber
assuming the limit on the right exists or is ∞ or −∞. This result also holds if the limit is infinite, if a=∞ or −∞, or the limit is one-sided.
Example \PageIndex{2}: Applying L’Hôpital’s Rule (∞/∞) Case
Evaluate each of the following limits by applying L’Hôpital’s rule.
- \displaystyle\lim_{x→\infty}\dfrac{3x+5}{2x+1}
- \displaystyle \lim_{x→0^+}\dfrac{\ln x}{\cot x}
Solution
a. Since 3x+5 and 2x+1 are first-degree polynomials with positive leading coefficients, \displaystyle\lim_{x→∞}(3x+5)=∞ and \displaystyle\lim_{x→∞}(2x+1)=∞. Therefore, we apply L’Hôpital’s rule and obtain
\lim_{x→∞}\dfrac{3x+5}{2x+1}=\lim_{x→∞}\dfrac{3}{2}=\dfrac{3}{2}.\nonumber
Note that this limit can also be calculated without invoking L’Hôpital’s rule. Earlier in the chapter we showed how to evaluate such a limit by dividing the numerator and denominator by the highest power of x in the denominator. In doing so, we saw that
\lim_{x→∞}\dfrac{3x+5}{2x+1}=\lim_{x→∞}\dfrac{3+5/x}{2+1/x}=\dfrac{3}{2}. \nonumber
L’Hôpital’s rule provides us with an alternative means of evaluating this type of limit.
b. Here, \displaystyle \lim_{x→0^+}\ln x=−∞ and \displaystyle \lim_{x→0^+}\cot x=∞. Therefore, we can apply L’Hôpital’s rule and obtain
\lim_{x→0^+}\dfrac{\ln x}{\cot x}=\lim_{x→0^+}\dfrac{1/x}{−\csc^2x}=\lim_{x→0^+}\dfrac{1}{−x \csc^2x}. \nonumber
Now as x→0^+, \csc^2x→∞. Therefore, the first term in the denominator is approaching zero and the second term is getting really large. In such a case, anything can happen with the product. Therefore, we cannot make any conclusion yet. To evaluate the limit, we use the definition of \csc x to write
\lim_{x→0^+}\dfrac{1}{−x \csc^2x}=\lim_{x→0^+}\dfrac{\sin^2x}{−x}. \nonumber
Now \displaystyle\lim_{x→0^+}\sin^2x=0 and \displaystyle\lim_{x→0^+}-x=0, so we apply L’Hôpital’s rule again. We find
\lim_{x→0^+}\dfrac{\sin^2x}{−x}=\lim_{x→0^+}\dfrac{2\sin x\cos x}{−1}=\dfrac{0}{−1}=0. \nonumber
We conclude that
\lim_{x→0^+}\dfrac{\ln x}{\cot x}=0. \nonumber
Exercise \PageIndex{2}
Evaluate \lim\limits_{x→∞} \dfrac{\ln x}{5x}.
- Hint
-
\dfrac{d}{dx}\big(\ln x\big)=\dfrac{1}{x}
- Answer
-
0
As mentioned, L’Hôpital’s rule is an extremely useful tool for evaluating limits. It is important to remember, however, that to apply L’Hôpital’s rule to a quotient \dfrac{f(x)}{g(x)}, it is essential that the limit of \dfrac{f(x)}{g(x)} be of the form \dfrac{0}{0} or ∞/∞. Consider the following example.
Example \PageIndex{3}: When L’Hôpital’s Rule Does Not Apply
Consider \displaystyle\lim_{x→1}\dfrac{x^2+5}{3x+4}.
Show that the limit cannot be evaluated by applying L’Hôpital’s rule.
Solution
Because the limits of the numerator and denominator are not both zero and are not both infinite, we cannot apply L’Hôpital’s rule. If we try to do so, we get
\dfrac{d}{dx}(x^2+5)=2x\nonumber
and
\dfrac{d}{dx}(3x+4)=3. \nonumber
At which point we would conclude erroneously that
\lim_{x→1}\dfrac{x^2+5}{3x+4}=\lim_{x→1}\dfrac{2x}{3}=\dfrac{2}{3}. \nonumber
However, since \displaystyle \lim_{x→1}(x^2+5)=6 and \displaystyle \lim_{x→1}(3x+4)=7, we actually have
\lim_{x→1}\dfrac{x^2+5}{3x+4}=\dfrac{6}{7}. \nonumber
We can conclude that
\lim_{x→1}\dfrac{x^2+5}{3x+4}≠\lim_{x→1}\dfrac{\dfrac{d}{dx}(x^2+5)}{\dfrac{d}{dx}(3x+4).} \nonumber
Exercise \PageIndex{3}
Explain why we cannot apply L’Hôpital’s rule to evaluate \displaystyle\lim_{x→0^+}\dfrac{\cos x}{x}. Evaluate \displaystyle\lim_{x→0^+}\dfrac{\cos x}{x} by other means.
- Hint
-
Determine the limits of the numerator and denominator separately.
- Answer
-
\displaystyle\lim_{x→0^+}\cos x=1. Therefore, we cannot apply L’Hôpital’s rule. The limit of the quotient is ∞.
Other Indeterminate Forms
L’Hôpital’s rule is very useful for evaluating limits involving the indeterminate forms \dfrac{0}{0} and ∞/∞. However, we can also use L’Hôpital’s rule to help evaluate limits involving other indeterminate forms that arise when evaluating limits. The expressions 0⋅∞, ∞−∞, 1^∞, ∞^0, and 0^0 are all considered indeterminate forms. These expressions are not real numbers. Rather, they represent forms that arise when trying to evaluate certain limits. Next we realize why these are indeterminate forms and then understand how to use L’Hôpital’s rule in these cases. The key idea is that we must rewrite the indeterminate forms in such a way that we arrive at the indeterminate form \dfrac{0}{0} or ∞/∞.
Indeterminate Form of Type 0⋅∞
Suppose we want to evaluate \displaystyle \lim_{x→a}(f(x)⋅g(x)), where f(x)→0 and g(x)→∞ (or −∞) as x→a. Since one term in the product is approaching zero but the other term is becoming arbitrarily large (in magnitude), anything can happen to the product. We use the notation 0⋅∞ to denote the form that arises in this situation. The expression 0⋅∞ is considered indeterminate because we cannot determine without further analysis the exact behavior of the product f(x)g(x) as x→∞. For example, let n be a positive integer and consider
f(x)=\dfrac{1}{(x^n+1)} and g(x)=3x^2.
As x→∞, f(x)→0 and g(x)→∞. However, the limit as x→∞ of f(x)g(x)=\dfrac{3x^2}{(x^n+1)} varies, depending on n. If n=2, then \displaystyle\lim_{x→∞}f(x)g(x)=3. If n=1, then \displaystyle\lim_{x→∞}f(x)g(x)=∞. If n=3, then \displaystyle\lim_{x→∞}f(x)g(x)=0. Here we consider another limit involving the indeterminate form 0⋅∞ and show how to rewrite the function as a quotient to use L’Hôpital’s rule.
Example \PageIndex{4}: Indeterminate Form of Type 0⋅∞
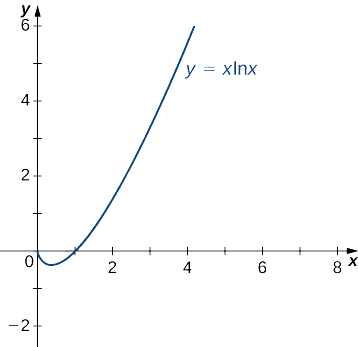
Evaluate \displaystyle \lim\limits_{x→0^+}x\ln x.
Solution
First, rewrite the function x\ln x as a quotient to apply L’Hôpital’s rule. If we write
x\ln x=\dfrac{\ln x}{1/x} \nonumber
we see that \ln x→−∞ as x→0^+ and \dfrac{1}{x}→∞ as x→0^+. Therefore, we can apply L’Hôpital’s rule and obtain
\lim_{x→0^+}\dfrac{\ln x}{1/x}=\lim_{x→0^+}\dfrac{\dfrac{d}{dx}\big(\ln x\big)}{\dfrac{d}{dx}\big(1/x\big)}=\lim_{x→0^+}\dfrac{1/x}{−1/x^2}=\lim_{x→0^+}(−x)=0. \nonumber
We conclude that
\lim_{x→0^+}x\ln x=0. \nonumber
Exercise \PageIndex{4}
Evaluate \lim\limits_{x→0}x\cot x.
- Hint
-
Write x\cot x=\dfrac{x \cos x}{\sin x}
- Answer
-
1
Indeterminate Form of Type ∞-∞
Another type of indeterminate form is ∞−∞. Consider the following example. Let n be a positive integer and let f(x)=3x^n and g(x)=3x^2+5. As x→∞, f(x)→∞ and g(x)→∞. We are interested in \displaystyle\lim_{x→∞}(f(x)−g(x)). Depending on whether f(x) grows faster, g(x) grows faster, or they grow at the same rate, as we see next, anything can happen in this limit. Since f(x)→∞ and g(x)→∞, we write ∞−∞ to denote the form of this limit. As with our other indeterminate forms, ∞−∞ has no meaning on its own and we must do more analysis to determine the value of the limit. For example, suppose the exponent n in the function f(x)=3x^n is n=3, then
\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x^3−3x^2−5)=∞. \nonumber
On the other hand, if n=2, then
\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x^2−3x^2−5)=−5. \nonumber
However, if n=1, then
\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x−3x^2−5)=−∞. \nonumber
Therefore, the limit cannot be determined by considering only ∞−∞. Next we see how to rewrite an expression involving the indeterminate form ∞−∞ as a fraction to apply L’Hôpital’s rule.
Example \PageIndex{5}: Indeterminate Form of Type ∞−∞
Evaluate \lim\limits_{x→0^+}\left(\dfrac{1}{x^2}−\dfrac{1}{\tan x}\right).
Solution
By combining the fractions, we can write the function as a quotient. Since the least common denominator is x^2\tan x, we have
\dfrac{1}{x^2}−\dfrac{1}{\tan x}=\dfrac{(\tan x)−x^2}{x^2\tan x}.
As x→0^+, the numerator \tan x−x^2→0 and the denominator x^2\tan x→0. Therefore, we can apply L’Hôpital’s rule. Taking the derivatives of the numerator and the denominator, we have
\lim_{x→0^+}\dfrac{(\tan x)−x^2}{x^2\tan x}=\lim_{x→0^+}\dfrac{(\sec^2x)−2x}{x^2\sec^2x+2x\tan x}. \nonumber
As x→0^+, (\sec^2x)−2x→1 and x^2\sec^2x+2x\tan x→0. Since the denominator is positive as x approaches zero from the right, we conclude that
\lim_{x→0^+}\dfrac{(\sec^2x)−2x}{x^2\sec^2x+2x\tan x}=∞. \nonumber
Therefore,
\lim_{x→0^+}\left(\dfrac{1}{x^2}−\dfrac{1}{\tan x}\right)=∞. \nonumber
Exercise \PageIndex{5}
Evaluate \displaystyle \lim_{x→0^+}\left(\dfrac{1}{x}−\dfrac{1}{\sin x}\right).
- Hint
-
Rewrite the difference of fractions as a single fraction.
- Answer
-
0
Indeterminate Forms Involving Exponents
Another type of indeterminate form that arises when evaluating limits involves exponents. The expressions 0^0, ∞^0, and 1^∞ are all indeterminate forms. On their own, these expressions are meaningless because we cannot actually evaluate these expressions as we would evaluate an expression involving real numbers. Rather, these expressions represent forms that arise when finding limits. Now we examine how L’Hôpital’s rule can be used to evaluate limits involving these indeterminate forms.
Since L’Hôpital’s rule applies to quotients, we use the natural logarithm function and its properties to reduce a problem evaluating a limit involving exponents to a related problem involving a limit of a quotient. For example, suppose we want to evaluate \displaystyle \lim_{x→a}f(x)^{g(x)} and we arrive at the indeterminate form ∞^0. (The indeterminate forms 0^0 and 1^∞ can be handled similarly.) We proceed as follows. Let
y=f(x)^{g(x)}. \nonumber
Then,
\ln y=\ln(f(x)^{g(x)})=g(x)\ln(f(x)). \nonumber
Therefore,
\lim_{x→a}[\ln(y)]=\lim_{x→a}[g(x)\ln(f(x))]. \nonumber
Since \displaystyle \lim_{x→a}f(x)=∞, we know that \displaystyle \lim_{x→a}\ln(f(x))=∞. Therefore, \displaystyle \lim_{x→a}g(x)\ln(f(x)) is of the indeterminate form 0⋅∞, and we can use the techniques discussed earlier to rewrite the expression g(x)\ln(f(x)) in a form so that we can apply L’Hôpital’s rule. Suppose \displaystyle \lim_{x→a}g(x)\ln(f(x))=L, where L may be ∞ or −∞. Then
\lim_{x→a}[\ln(y)]=L. \nonumber
Since the natural logarithm function is continuous, we conclude that
\ln\left(\lim_{x→a}y\right)=L, \nonumber
which gives us
\lim_{x→a}y=\lim_{x→a}f(x)^{g(x)}=e^L. \nonumber
Example \PageIndex{6}: Indeterminate Form of Type ∞^0
Evaluate \lim\limits_{x→∞}x^{1/x}.
Solution
Let y=x^{1/x}.Then,
\ln(x^{1/x})=\dfrac{1}{x}\ln x=\dfrac{\ln x}{x}. \nonumber
We need to evaluate \displaystyle \lim_{x→∞}\dfrac{\ln x}{x}. Applying L’Hôpital’s rule, we obtain
\lim_{x→∞}\ln y=\lim_{x→∞}\dfrac{\ln x}{x}=\lim_{x→∞}\dfrac{1/x}{1}=0. \nonumber
Therefore, \displaystyle \lim_{x→∞}\ln y=0. Since the natural logarithm function is continuous, we conclude that
\ln\left(\lim_{x→∞}y\right)=0, \nonumber
which leads to
\lim_{x→∞}x^{1/x}=\lim_{x→∞}y=e^{\ln\left(\displaystyle\lim_{x→∞}y\right)}=e^0=1. \nonumber
Hence,
\lim_{x→∞}x^{1/x}=1. \nonumber
Exercise \PageIndex{6}
Evaluate \lim\limits_{x→∞}x^{1/\ln(x)}.
- Hint
-
Let y=x^{1/\ln(x)} and apply the natural logarithm to both sides of the equation.
- Answer
-
e
Example \PageIndex{7}: Indeterminate Form of Type 0^0
Evaluate \lim\limits_{x→0^+}x^{\sin x}.
Solution
Let
y=x^{\sin x}. \nonumber
Therefore,
\ln y=\ln(x^{\sin x})=\sin x\ln x. \nonumber
We now evaluate \displaystyle\lim_{x→0^+}\sin x\ln x. Since \displaystyle\lim_{x→0^+}\sin x=0 and \displaystyle\lim_{x→0^+}\ln x=−∞, we have the indeterminate form 0⋅∞. To apply L’Hôpital’s rule, we need to rewrite \sin x\ln x as a fraction. We could write
\sin x\ln x=\dfrac{\sin x}{1/\ln x} \nonumber
or
\sin x\ln x=\dfrac{\ln x}{1/\sin x}=\dfrac{\ln x}{\csc x}. \nonumber
Let’s consider the first option. In this case, applying L’Hôpital’s rule, we would obtain
\lim_{x→0^+}\sin x\ln x=\lim_{x→0^+}\dfrac{\sin x}{1/\ln x}=\lim_{x→0^+}\dfrac{\cos x}{−1/(x(\ln x)^2)}=\lim_{x→0^+}(−x(\ln x)^2\cos x).\nonumber
Unfortunately, we not only have another expression involving the indeterminate form 0⋅∞, but the new limit is even more complicated to evaluate than the one with which we started. Instead, we try the second option. By writing
\sin x\ln x=\dfrac{\ln x}{1/\sin x}=\dfrac{\ln x}{\csc x,} \nonumber
and applying L’Hôpital’s rule, we obtain
\lim_{x→0^+}\sin x\ln x=\lim_{x→0^+}\dfrac{\ln x}{\csc x}=\lim_{x→0^+}\dfrac{1/x}{−\csc x\cot x}=\lim_{x→0^+}\dfrac{−1}{x\csc x\cot x}. \nonumber
Using the fact that \csc x=\dfrac{1}{\sin x} and \cot x=\dfrac{\cos x}{\sin x}, we can rewrite the expression on the right-hand side as
\lim_{x→0^+}\dfrac{−\sin^2x}{x\cos x}=\lim_{x→0^+}\left[\dfrac{\sin x}{x}⋅(−\tan x)\right]=\left(\lim_{x→0^+}\dfrac{\sin x}{x}\right)⋅\left(\lim_{x→0^+}(−\tan x)\right)=1⋅0=0. \nonumber
We conclude that \displaystyle\lim_{x→0^+}\ln y=0. Therefore, \displaystyle\ln\left(\lim_{x→0^+}y\right)=0 and we have
\lim_{x→0^+}y=\lim_{x→0^+}x^{\sin x}=e^0=1.\nonumber
Hence,
\lim_{x→0^+}x^{\sin x}=1. \nonumber
Exercise \PageIndex{7}
Evaluate \displaystyle \lim_{x→0^+}x^x.
- Hint
-
Let y=x^x and take the natural logarithm of both sides of the equation.
- Answer
-
1
Growth Rates of Functions
Suppose the functions f and g both approach infinity as x→∞. Although the values of both functions become arbitrarily large as the values of x become sufficiently large, sometimes one function is growing more quickly than the other. For example, f(x)=x^2 and g(x)=x^3 both approach infinity as x→∞. However, as Table \PageIndex{1} shows, the values of x^3 are growing much faster than the values of x^2.
| x | 10 | 100 | 1000 | 10,000 |
|---|---|---|---|---|
| f(x)=x^2 | 100 | 10,000 | 1,000,000 | 100,000,000 |
| g(x)=x^3 | 1000 | 1,000,000 | 1,000,000,000 | 1,000,000,000,000 |
In fact,
\lim_{x→∞}\dfrac{x^3}{x^2}=\lim_{x→∞}x=∞. \nonumber
or, equivalently
\lim_{x→∞}\dfrac{x^2}{x^3}=\lim_{x→∞}\dfrac{1}{x}=0. \nonumber
As a result, we say x^3 is growing more rapidly than x^2 as x→∞. On the other hand, for f(x)=x^2 and g(x)=3x^2+4x+1, although the values of g(x) are always greater than the values of f(x) for x>0, each value of g(x) is roughly three times the corresponding value of f(x) as x→∞, as shown in Table \PageIndex{2}. In fact,
\lim_{x→∞}\dfrac{x^2}{3x^2+4x+1}=\dfrac{1}{3}. \nonumber
| x | 10 | 100 | 1000 | 10,000 |
|---|---|---|---|---|
| f(x)=x^2 | 100 | 10,000 | 1,000,000 | 100,000,000 |
| g(x)=3x^2+4x+1 | 341 | 30,401 | 3,004,001 | 300,040,001 |
In this case, we say that x^2 and 3x^2+4x+1 are growing at the same rate as x→∞.
More generally, suppose f and g are two functions that approach infinity as x→∞. We say g grows more rapidly than f as x→∞ if
\lim_{x→∞}\dfrac{g(x)}{f(x)}=∞ \quad \text{or, equivalently,} \quad \lim_{x→∞}\dfrac{f(x)}{g(x)}=0. \nonumber
On the other hand, if there exists a constant M≠0 such that
\lim_{x→∞}\dfrac{f(x)}{g(x)}=M, \nonumber
we say f and g grow at the same rate as x→∞.
Next we see how to use L’Hôpital’s rule to compare the growth rates of power, exponential, and logarithmic functions.
Example \PageIndex{8}: Comparing the Growth Rates of \ln(x), x^2, and e^x
For each of the following pairs of functions, use L’Hôpital’s rule to evaluate \lim_{x→∞}\dfrac{f(x)}{g(x)}. \nonumber
- f(x)=x^2 and g(x)=e^x
- f(x)=\ln(x) and g(x)=x^2
Solution
a. Since \displaystyle \lim_{x→∞}x^2=∞ and \displaystyle \lim_{x→∞}e^x=∞, we can use L’Hôpital’s rule to evaluate \displaystyle \lim_{x→∞}\left[\dfrac{x^2}{e^x}\right]. We obtain
\lim_{x→∞}\frac{x^2}{e^x}=\lim_{x→∞}\frac{2x}{e^x}. \nonumber
Since \displaystyle \lim_{x→∞}2x=∞ and \displaystyle \lim_{x→∞}e^x=∞, we can apply L’Hôpital’s rule again. Since
\lim_{x→∞}\frac{2x}{e^x}=\lim_{x→∞}\frac{2}{e^x}=0, \nonumber
we conclude that
\lim_{x→∞}\dfrac{x^2}{e^x}=0. \nonumber
Therefore, e^x grows more rapidly than x^2 as x→∞ (See Figure \PageIndex{3} and Table \PageIndex{3})
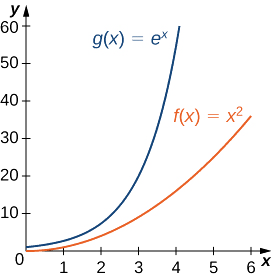
| x | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| x^2 | 25 | 100 | 225 | 400 |
| e^x | 148 | 22,026 | 3,269,017 | 485,165,195 |
b. Since \displaystyle \lim_{x→∞}\ln x=∞ and \displaystyle \lim_{x→∞}x^2=∞, we can use L’Hôpital’s rule to evaluate \displaystyle \lim_{x→∞}\dfrac{\ln x}{x^2}. We obtain
\lim_{x→∞}\dfrac{\ln x}{x^2}=\lim_{x→∞}\dfrac{1/x}{2x}=\lim_{x→∞}\dfrac{1}{2x^2}=0. \nonumber
Thus, x^2 grows more rapidly than \ln x as x→∞ (see Figure \PageIndex{4} and Table \PageIndex{4}).
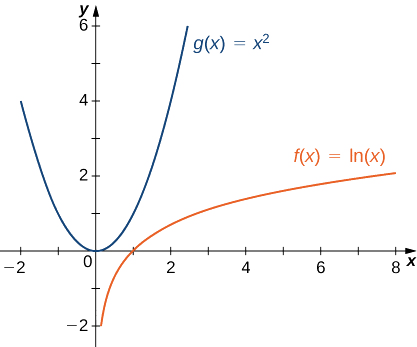
| x | 10 | 100 | 1000 | 10,000 |
|---|---|---|---|---|
| \ln(x) | 2.303 | 4.605 | 6.908 | 9.210 |
| x^2 | 100 | 10,000 | 1,000,000 | 100,000,000 |
Exercise \PageIndex{8}
Compare the growth rates of x^{100} and 2^x.
- Hint
-
Apply L’Hôpital’s rule to x^{100}/2^x.
- Answer
-
The function 2^x grows faster than x^{100}.
Using the same ideas as in Example \PageIndex{8}a. it is not difficult to show that e^x grows more rapidly than x^p for any p>0. In Figure \PageIndex{5} and Table \PageIndex{5}, we compare e^x with x^3 and x^4 as x→∞.
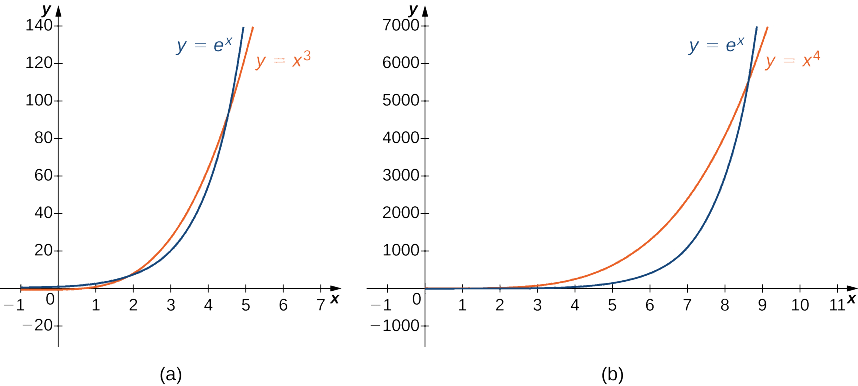
| x | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| x^3 | 125 | 1000 | 3375 | 8000 |
| x^4 | 625 | 10,000 | 50,625 | 160,000 |
| e^x | 148 | 22,026 | 3,269,017 | 485,165,195 |
Similarly, it is not difficult to show that x^p grows more rapidly than \ln x for any p>0. In Figure \PageIndex{6} and Table \PageIndex{6}, we compare \ln x with \sqrt[3]{x} and \sqrt{x}.
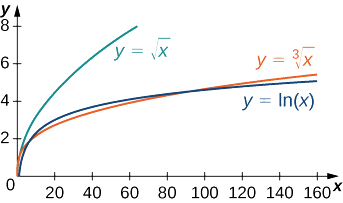
| x | 10 | 100 | 1000 | 10,000 |
|---|---|---|---|---|
| \ln(x) | 2.303 | 4.605 | 6.908 | 9.210 |
| \sqrt[3]{x} | 2.154 | 4.642 | 10 | 21.544 |
| \sqrt{x} | 3.162 | 10 | 31.623 | 100 |
Key Concepts
- L’Hôpital’s rule can be used to evaluate the limit of a quotient when the indeterminate form \dfrac{0}{0} or ∞/∞ arises.
- L’Hôpital’s rule can also be applied to other indeterminate forms if they can be rewritten in terms of a limit involving a quotient that has the indeterminate form \dfrac{0}{0} or ∞/∞.
- The exponential function e^x grows faster than any power function x^p, p>0.
- The logarithmic function \ln x grows more slowly than any power function x^p, p>0.
Glossary
- indeterminate forms
- When evaluating a limit, the forms \dfrac{0}{0},∞/∞, 0⋅∞, ∞−∞, 0^0, ∞^0, and 1^∞ are considered indeterminate because further analysis is required to determine whether the limit exists and, if so, what its value is.
- L’Hôpital’s rule
- If f and g are differentiable functions over an interval a, except possibly at a, and \displaystyle \lim_{x→a}f(x)=0=\lim_{x→a}g(x) or \displaystyle \lim_{x→a}f(x) and \displaystyle \lim_{x→a}g(x) are infinite, then \displaystyle \lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)}, assuming the limit on the right exists or is ∞ or −∞.

