5.2: Constant Coefficient Homogeneous Equations
- Last updated
- Save as PDF
- Page ID
- 30724
This section deals with homogeneous equations of the special form $$ ay''+by'+cy=0, $$ where \(a\), \(b\), and \(c\) are constant (\(a\ne0\)). When you've completed this section you'll know everything there is to know about solving such equations.
If \(a,b\), and \(c\) are real constants and \(a\ne0\), then
\[ay''+by'+cy=F(x)\nonumber \]
is said to be a constant coefficient equation. In this section we consider the homogeneous constant coefficient equation
\[\label{eq:5.2.1} ay''+by'+cy=0.\]
As we’ll see, all solutions of Equation \ref{eq:5.2.1} are defined on \((-\infty,\infty)\). This being the case, we’ll omit references to the interval on which solutions are defined, or on which a given set of solutions is a fundamental set, etc., since the interval will always be \((-\infty,\infty)\).
The key to solving Equation \ref{eq:5.2.1} is that if \(y=e^{rx}\) where \(r\) is a constant then the left side of Equation \ref{eq:5.2.1} is a multiple of \(e^{rx}\); thus, if \(y=e^{rx}\) then \(y'=re^{rx}\) and \(y''=r^2e^{rx}\), so
\[\label{eq:5.2.2} ay''+by'+cy=ar^2e^{rx}+bre^{rx}+ce^{rx}=(ar^2+br+c)e^{rx}.\]
The quadratic polynomial
\[p(r)=ar^2+br+c\nonumber \]
is the characteristic polynomial of Equation \ref{eq:5.2.1}, and \(p(r)=0\) is the characteristic equation. From Equation \ref{eq:5.2.2} we can see that \(y=e^{rx}\) is a solution of Equation \ref{eq:5.2.1} if and only if \(p(r)=0\).
The roots of the characteristic equation are given by the quadratic formula
\[\label{eq:5.2.3} r={-b\pm\sqrt{b^2-4ac}\over2a}.\]
Consider Three Cases
- Case 1: \(b^2-4ac>0\), so the characteristic equation has two distinct real roots.
- Case 2: \(b^2-4ac=0\), so the characteristic equation has a repeated real root.
- Case 3: \(b^2-4ac<0\), so the characteristic equation has complex roots.
In each case we’ll start with an example.
Case 1: Distinct Real Roots
Example 5.2.1
- Find the general solution of \[\label{eq:5.2.4} y''+6y'+5y=0.\]
- Solve the initial value problem \[\label{eq:5.2.5} y''+6y'+5y=0, \quad y(0)=3,\; y'(0)=-1.\]
Solution
a. The characteristic polynomial of Equation \ref{eq:5.2.4} is
\[p(r)=r^2+6r+5=(r+1)(r+5).\nonumber\]
Since \(p(-1)=p(-5)=0\), \(y_1=e^{-x}\) and \(y_2=e^{-5x}\) are solutions of Equation \ref{eq:5.2.4}. Since \(y_2/y_1=e^{-4x}\) is nonconstant, Theorem 5.1.6 implies that the general solution of Equation \ref{eq:5.2.4} is
\[\label{eq:5.2.6} y=c_1e^{-x}+c_2e^{-5x}.\]
b. We must determine \(c_1\) and \(c_2\) in Equation \ref{eq:5.2.6} so that \(y\) satisfies the initial conditions in Equation \ref{eq:5.2.5}. Differentiating Equation \ref{eq:5.2.6} yields
\[\label{eq:5.2.7} y'=-c_1e^{-x}-5c_2e^{-5x}.\]
Imposing the initial conditions \(y(0)=3,\, y'(0)=-1\) in Equation \ref{eq:5.2.6} and Equation \ref{eq:5.2.7} yields
\[\begin{array}{rcr} \phantom{-}c_1+\phantom{5}c_2 & = & 3\phantom{.}\\ -c_1-5c_2 & = & -1. \end{array}\nonumber \]
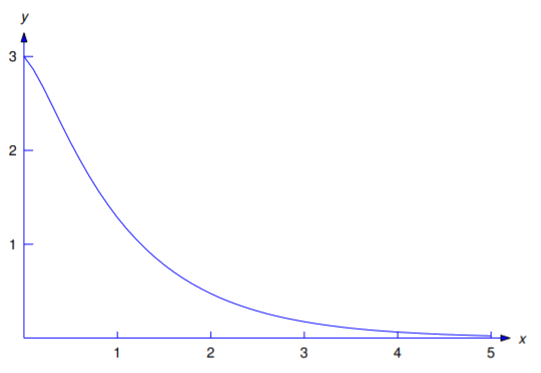
The solution of this system is \(c_1=7/2,c_2=-1/2\). Therefore the solution of Equation \ref{eq:5.2.5} is
\[y={7\over2}e^{-x}-{1\over2}e^{-5x}.\nonumber \]
Figure 5.2.1 is a graph of this solution.
If the characteristic equation has arbitrary distinct real roots \(r_1\) and \(r_2\), then \(y_1=e^{r_1x}\) and \(y_2=e^{r_2x}\) are solutions of \(ay''+by'+cy=0\). Since \(y_2/y_1=e^{(r_2-r_1)x}\) is nonconstant, Theorem 5.1.6 implies that \(\{y_1,y_2\}\) is a fundamental set of solutions of \(ay''+by'+cy=0\).
Case 2: A Repeated Real Root
Example 5.2.2
- Find the general solution of \[\label{eq:5.2.8} y''+6y'+9y=0.\]
- Solve the initial value problem \[\label{eq:5.2.9} y''+6y'+9y=0, \quad y(0)=3,\; y'(0)=-1.\]
Solution
a. The characteristic polynomial of Equation \ref{eq:5.2.8} is
\[p(r)=r^2+6r+9=(r+3)^2,\nonumber \]
so the characteristic equation has the repeated real root \(r_1=-3\). Therefore \(y_1=e^{-3x}\) is a solution of Equation \ref{eq:5.2.8}. Since the characteristic equation has no other roots, Equation \ref{eq:5.2.8} has no other solutions of the form \(e^{rx}\). We look for solutions of the form \(y=uy_1=ue^{-3x}\), where \(u\) is a function that we’ll now determine. (This should remind you of the method of variation of parameters used in Section 2.1 to solve the nonhomogeneous equation \(y'+p(x)y=f(x)\), given a solution \(y_1\) of the complementary equation \(y'+p(x)y=0\). It’s also a special case of a method called reduction of order that we’ll study in Section 5.6. For other ways to obtain a second solution of Equation \ref{eq:5.2.8} that’s not a multiple of \(e^{-3x}\), see Exercises 5.1.9, 5.1.12, and 5.1.33.
If \(y=ue^{-3x}\), then
\[y'=u'e^{-3x}-3ue^{-3x}\quad \text{and} \quad y''=u''e^{-3x}-6u'e^{-3x}+9ue^{-3x},\nonumber \]
so
\[\begin{aligned} y''+6y'+9y&=e^{-3x}\left[(u''-6u'+9u)+6(u'-3u)+9u\right]\\ &=e^{-3x}\left[u''-(6-6)u'+(9-18+9)u\right]=u''e^{-3x}.\end{aligned}\nonumber \]
Therefore \(y=ue^{-3x}\) is a solution of Equation \ref{eq:5.2.8} if and only if \(u''=0\), which is equivalent to \(u=c_1+c_2x\), where \(c_1\) and \(c_2\) are constants. Therefore any function of the form
\[\label{eq:5.2.10} y=e^{-3x}(c_1+c_2x)\]
is a solution of Equation \ref{eq:5.2.8}. Letting \(c_1=1\) and \(c_2=0\) yields the solution \(y_1=e^{-3x}\) that we already knew. Letting \(c_1=0\) and \(c_2=1\) yields the second solution \(y_2=xe^{-3x}\). Since \(y_2/y_1=x\) is nonconstant, Theorem 5.1.6 implies that \(\{y_1,y_2\}\) is fundamental set of solutions of Equation \ref{eq:5.2.8}, and Equation \ref{eq:5.2.10} is the general solution.
b. Differentiating Equation \ref{eq:5.2.10} yields
\[\label{eq:5.2.11} y'=-3e^{-3x}(c_1+c_2x)+c_2e^{-3x}.\]
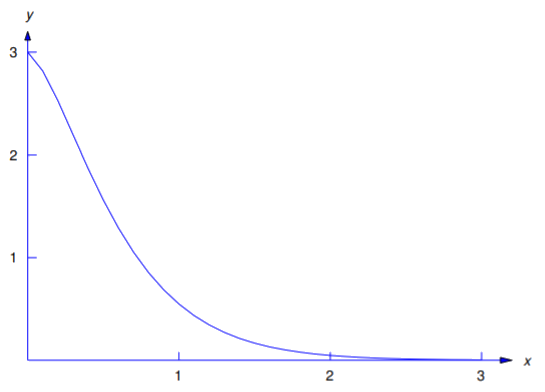
Imposing the initial conditions \(y(0)=3,\, y'(0)=-1\) in Equation \ref{eq:5.2.10} and Equation \ref{eq:5.2.11} yields \(c_1=3\) and \(-3c_1+c_2=-1\), so \(c_2=8\). Therefore the solution of Equation \ref{eq:5.2.9} is
\[y=e^{-3x}(3+8x).\nonumber \]
Figure 5.2.2 is a graph of this solution.
If the characteristic equation of \(ay''+by'+cy=0\) has an arbitrary repeated root \(r_1\), the characteristic polynomial must be
\[p(r)=a(r-r_1)^2=a(r^2-2r_1r+r_1^2).\nonumber \]
Therefore
\[ar^2+br+c=ar^2-(2ar_1)r+ar_1^2,\nonumber \]
which implies that \(b=-2ar_1\) and \(c=ar_1^2\). Therefore \(ay''+by'+cy=0\) can be written as \(a(y''-2r_1y'+r_1^2y)=0\). Since \(a\ne0\) this equation has the same solutions as
\[\label{eq:5.2.12} y''-2r_1y'+r_1^2y=0.\]
Since \(p(r_1)=0\), t \(y_1=e^{r_1x}\) is a solution of \(ay''+by'+cy=0\), and therefore of Equation \ref{eq:5.2.12}. Proceeding as in Example 5.2.1 , we look for other solutions of Equation \ref{eq:5.2.12} of the form \(y=ue^{r_1x}\); then
\[y'=u'e^{r_1x}+rue^{r_1x}\quad \text{and} \quad y''=u''e^{r_1x}+2r_1u'e^{r_1x}+r_1^2ue^{r_1x},\nonumber \]
so
\[\begin{aligned} y''-2r_1y'+r_1^2y &=e^{rx}\left[(u''+2r_1u'+r_1^2u)- 2r_1(u'+r_1u)+r_1^2u\right]\\ &=e^{r_1x}\left[u''+(2r_1-2r_1)u'+(r_1^2-2r_1^2+r_1^2)u\right]=u''e^{r_1x}.\end{aligned}\]
Therefore \(y=ue^{r_1x}\) is a solution of Equation \ref{eq:5.2.12} if and only if \(u''=0\), which is equivalent to \(u=c_1+c_2x\), where \(c_1\) and \(c_2\) are constants. Hence, any function of the form
\[\label{eq:5.2.13} y=e^{r_1x}(c_1+c_2x)\]
is a solution of Equation \ref{eq:5.2.12}. Letting \(c_1=1\) and \(c_2=0\) here yields the solution \(y_1=e^{r_1x}\) that we already knew. Letting \(c_1=0\) and \(c_2=1\) yields the second solution \(y_2=xe^{r_1x}\). Since \(y_2/y_1=x\) is nonconstant, Theorem 5.1.6 implies that \(\{y_1,y_2\}\) is a fundamental set of solutions of Equation \ref{eq:5.2.12}, and Equation \ref{eq:5.2.13} is the general solution.
Case 3: Complex Conjugate Roots
Example 5.2.3
- Find the general solution of \[\label{eq:5.2.14} y''+4y'+13y=0.\]
- Solve the initial value problem \[\label{eq:5.2.15} y''+4y'+13y=0, \quad y(0)=2,\; y'(0)=-3.\]
Solution
a. The characteristic polynomial of Equation \ref{eq:5.2.14} is
\[p(r)=r^2+4r+13=r^2+4r+4+9=(r+2)^2+9.\nonumber \]
The roots of the characteristic equation are \(r_1=-2+3i\) and \(r_2=-2-3i\). By analogy with Case 1, it is reasonable to expect that \(e^{(-2+3i)x}\) and \(e^{(-2-3i)x}\) are solutions of Equation \ref{eq:5.2.14}. This is true (see Exercise 5.2.34); however, there are difficulties here, since you are probably not familiar with exponential functions with complex arguments, and even if you are, it is inconvenient to work with them, since they are complex–valued. We’ll take a simpler approach, which we motivate as follows: the exponential notation suggests that
\[e^{(-2+3i)x}=e^{-2x}e^{3ix}\quad \text{and} \quad e^{(-2-3i)x}=e^{-2x}e^{-3ix},\nonumber \]
so even though we haven’t defined \(e^{3ix}\) and \(e^{-3ix}\), it is reasonable to expect that every linear combination of \(e^{(-2+3i)x}\) and \(e^{(-2-3i)x}\) can be written as \(y=ue^{-2x}\), where \(u\) depends upon \(x\). To determine \(u\), we note that if \(y=ue^{-2x}\) then
\[y'=u'e^{-2x}-2ue^{-2x}\quad \text{and} \quad y''=u''e^{-2x}-4u'e^{-2x}+4ue^{-2x},\nonumber \]
so
\[\begin{aligned} y''+4y'+13y&=e^{-2x}\left[(u''-4u'+4u)+4(u'-2u)+13u\right]\\ &=e^{-2x}\left[u''-(4-4)u'+(4-8+13)u\right]=e^{-2x}(u''+9u).\end{aligned}\nonumber \]
Therefore \(y=ue^{-2x}\) is a solution of Equation \ref{eq:5.2.14} if and only if
\[u''+9u=0.\nonumber \]
From Example 5.1.2, the general solution of this equation is
\[u=c_1\cos 3x +c_2\sin 3x. \nonumber \]
Therefore any function of the form
\[\label{eq:5.2.16} y=e^{-2x}(c_1\cos 3x+c_2\sin 3x)\]
is a solution of Equation \ref{eq:5.2.14}. Letting \(c_1=1\) and \(c_2=0\) yields the solution \(y_1=e^{-2x}\cos3x\). Letting \(c_1=0\) and \(c_2=1\) yields the second solution \(y_2=e^{-2x}\sin3x\). Since \(y_2/y_1=\tan3x\) is nonconstant, Theorem 5.1.6 implies that \(\{y_1,y_2\}\) is a fundamental set of solutions of Equation \ref{eq:5.2.14}, and Equation \ref{eq:5.2.16} is the general solution.
b. Imposing the condition \(y(0)=2\) in Equation \ref{eq:5.2.16} shows that \(c_1=2\). Differentiating Equation \ref{eq:5.2.16} yields
\[y'=-2e^{-2x}(c_1\cos 3x+c_2\sin 3x) +3e^{-2x}(-c_1\sin 3x +c_2\cos 3x),\nonumber \]
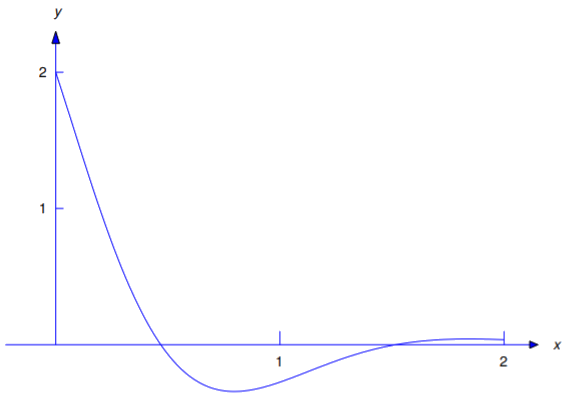
and imposing the initial condition \(y'(0)=-3\) here yields \(-3=-2c_1+3c_2=-4+3c_2\), so \(c_2=1/3\). Therefore the solution of Equation \ref{eq:5.2.15} is
\[y=e^{-2x}(2\cos 3x+ {1\over3}\sin 3x).\nonumber \]
Figure 5.2.3 is a graph of this function.
Now suppose the characteristic equation of \(ay''+by'+cy=0\) has arbitrary complex roots; thus, \(b^2-4ac<0\) and, from Equation \ref{eq:5.2.3}, the roots are
\[r_1 = {-b+i\sqrt{4ac-b^2}\over 2a},\quad r_2 = {-b-i\sqrt{4ac-b^2}\over 2a},\nonumber \]
which we rewrite as
\[\label{eq:5.2.17} r_1=\lambda+i \omega,\quad r_2 = \lambda - i \omega,\]
with
\[\lambda = -{b\over 2a},\quad \omega = {\sqrt{4ac-b^2}\over 2a}.\nonumber \]
Don’t memorize these formulas. Just remember that \(r_1\) and \(r_2\) are of the form Equation \ref{eq:5.2.17}, where \(\lambda\) is an arbitrary real number and \(\omega\) is positive; \(\lambda\) and \(\omega\) are the real and imaginary parts, respectively, of \(r_1\). Similarly, \(\lambda\) and \(-\omega\) are the real and imaginary parts of \(r_2\). We say that \(r_1\) and \(r_2\) are complex conjugates,
which means that they have the same real part and their imaginary parts have the same absolute values, but opposite signs.
As in Example 5.2.3 , it is reasonable to to expect that the solutions of \(ay''+by'+cy=0\) are linear combinations of \(e^{(\lambda+i\omega)x}\) and \(e^{(\lambda-i\omega)x}\). Again, the exponential notation suggests that
\[e^{(\lambda+i\omega)x}=e^{\lambda x}e^{i\omega x}\quad \text{and} \quad e^{(\lambda-i\omega)x}=e^{\lambda x}e^{-i\omega x},\nonumber \]
so even though we haven’t defined \(e^{i\omega x}\) and \(e^{-i\omega x}\), it is reasonable to expect that every linear combination of \(e^{(\lambda+i\omega)x}\) and \(e^{(\lambda-i\omega)x}\) can be written as \(y=ue^{\lambda x}\), where \(u\) depends upon \(x\). To determine \(u\) we first observe that since \(r_1=\lambda+i\omega\) and \(r_2=\lambda-i\omega\) are the roots of the characteristic equation, \(p\) must be of the form
\[\begin{align*} p(r)&=a(r-r_1)(r-r_2)\\[4pt] &=a(r-\lambda-i\omega)(r-\lambda+i\omega) \\[4pt] &= a \left[(r-\lambda)^2+\omega^2\right] \\[4pt] &=a(r^2-2\lambda r +\lambda^2+\omega^2). \end{align*} \]
Therefore \(ay''+by'+cy=0\) can be written as
\[a\left[y''-2\lambda y'+(\lambda^2+\omega^2)y\right]=0.\nonumber \]
Since \(a\ne0\) this equation has the same solutions as
\[\label{eq:5.2.18} y''-2\lambda y'+(\lambda^2+\omega^2)y=0.\]
To determine \(u\) we note that if \(y=ue^{\lambda x}\) then
\[y'=u'e^{\lambda x}+\lambda ue^{\lambda x}\quad \text{and} \quad y''=u''e^{\lambda x}+2\lambda u'e^{\lambda x}+\lambda^2ue^{\lambda x}.\nonumber \]
Substituting these expressions into Equation \ref{eq:5.2.18} and dropping the common factor \(e^{\lambda x}\) yields
\[(u''+2\lambda u'+\lambda^2 u)-2\lambda(u'+\lambda u) +(\lambda^2+\omega^2)u=0,\nonumber \]
which simplifies to
\[u''+\omega^2 u=0.\nonumber \]
From Example 5.1.2, the general solution of this equation is
\[u=c_1\cos\omega x +c_2\sin\omega x.\nonumber \]
Therefore any function of the form
\[\label{eq:5.2.19} y=e^{\lambda x}(c_1\cos\omega x+c_2\sin\omega x)\]
is a solution of Equation \ref{eq:5.2.18}. Letting \(c_1=1\) and \(c_2=0\) here yields the solution \(y_1=e^{\lambda x}\cos\omega x\). Letting \(c_1=0\) and \(c_2=1\) yields a second solution \(y_2=e^{\lambda x}\sin\omega x\). Since \(y_2/y_1=\tan\omega x\) is nonconstant, so Theorem 5.1.6 implies that \(\{y_1,y_2\}\) is a fundamental set of solutions of Equation \ref{eq:5.2.18}, and Equation \ref{eq:5.2.19} is the general solution.
Summary
The next theorem summarizes the results of this section.
Theorem 5.2.1
Let \(p(r)=ar^2+br+c\) be the characteristic polynomial of
\[\label{eq:5.2.20} ay''+by'+cy=0.\]
Then:- If \(p(r)=0\) has distinct real roots \(r_1\) and \(r_2,\) then the general solution of Equation \ref{eq:5.2.20} is \[y=c_1e^{r_1x}+c_2e^{r_2x}.\nonumber \]
- If \(p(r)=0\) has a repeated root \(r_1,\) then the general solution of Equation \ref{eq:5.2.20} is \[y=e^{r_1x}(c_1+c_2x).\nonumber \]
- If \(p(r)=0\) has complex conjugate roots \(r_1=\lambda+i\omega\) and \(r_2=\lambda-i\omega\) \((\)where \(\omega>0),\) then the general solution of Equation \ref{eq:5.2.20} is \[y=e^{\lambda x}(c_1\cos\omega x+c_2\sin\omega x).\nonumber \]


