8.6: Convolution

In this section we consider the problem of finding the inverse Laplace transform of a product \(H(s)=F(s)G(s)\), where \(F\) and \(G\) are the Laplace transforms of known functions \(f\) and \(g\). To motivate our interest in this problem, consider the initial value problem

\[ay''+by'+cy=f(t),\quad y(0)=0,\quad y'(0)=0.\nonumber \]

Taking Laplace transforms yields

\[(as^2+bs+c)Y(s)=F(s),\nonumber \]

so

\[\label{eq:8.6.1} Y(s)=F(s)G(s),\]

where

\[G(s)={1\over as^2+bs+c}.\nonumber \]

Until now wen’t been interested in the factorization indicated in Equation \ref{eq:8.6.1}, since we dealt only with differential equations with specific forcing functions. Hence, we could simply do the indicated multiplication in Equation \ref{eq:8.6.1} and use the table of Laplace transforms to find \(y={\mathscr L}^{-1}(Y)\). However, this isn’t possible if we want a formula for \(y\) in terms of \(f\), which may be unspecified.

To motivate the formula for \({\mathscr L}^{-1}(FG)\), consider the initial value problem

\[\label{eq:8.6.2} y'-ay=f(t),\quad y(0)=0,\]

which we first solve without using the Laplace transform. The solution of the differential equation in Equation \ref{eq:8.6.2} is of the form \(y=ue^{at}\) where

\[u'=e^{-at}f(t).\nonumber \]

Integrating this from \(0\) to \(t\) and imposing the initial condition \(u(0)=y(0)=0\) yields

\[u=\int_0^t e^{-a\tau}f(\tau)\,d\tau.\nonumber \]

Therefore

\[\label{eq:8.6.3} y(t)=e^{at}\int_0^t e^{-a\tau}f(\tau)\,d\tau=\int_0^t e^{a(t-\tau)}f(\tau)\,d\tau.\]

Now we’ll use the Laplace transform to solve Equation \ref{eq:8.6.2} and compare the result to Equation \ref{eq:8.6.3}. Taking Laplace transforms in Equation \ref{eq:8.6.2} yields

\[(s-a)Y(s)=F(s),\nonumber \]

so

\[Y(s)=F(s) {1\over s-a},\nonumber \]

which implies that

\[\label{eq:8.6.4} y(t)= {\mathscr L}^{-1}\left(F(s){1\over s-a}\right).\]

If we now let \(g(t)=e^{at}\), so that

\[G(s)={1\over s-a},\nonumber \]

then Equation \ref{eq:8.6.3} and Equation \ref{eq:8.6.4} can be written as

\[y(t)=\int_0^tf(\tau)g(t-\tau)\,d\tau\nonumber \]

and

\[y={\mathscr L}^{-1}(FG),\nonumber \]

respectively. Therefore

\[\label{eq:8.6.5} {\mathscr L}^{-1}(FG)=\int_0^t f(\tau)g(t-\tau)\,d\tau\]

in this case.

This motivates the next definition.

Definition 8.6.1 : Convolution

The convolution \(f*g\) of two functions \(f\) and \(g\) is defined by

\[(f*g)(t)=\int_0^t f(\tau)g(t-\tau)\,d\tau.\nonumber \]

It can be shown (Exercise 8.6.6) that \(f\ast g=g\ast f\); that is,

\[\int_0^tf(t-\tau)g(\tau)\,d\tau=\int_0^tf(\tau)g(t-\tau)\,d\tau. \nonumber\]

Equation \ref{eq:8.6.5} shows that \({\mathscr L}^{-1}(FG)=f*g\) in the special case where \(g(t)=e^{at}\). This next theorem states that this is true in general.

Theorem 8.6.2 : The Convolution Theorem

If \({\mathscr L}(f)=F\) and \({\mathscr L}(g)=G,\) then

\[{\mathscr L}(f*g)=FG.\nonumber \]

A complete proof of the convolution theorem is beyond the scope of this book. However, we’ll assume that \(f\ast g\) has a Laplace transform and verify the conclusion of the theorem in a purely computational way. By the definition of the Laplace transform,

\[{\mathscr L}(f\ast g)=\int_0^\infty e^{-st}(f\ast g)(t)\,dt=\int_0^\infty e^{-st} \int_0^t f(\tau)g(t-\tau)\,d\tau\,dt.\nonumber \]

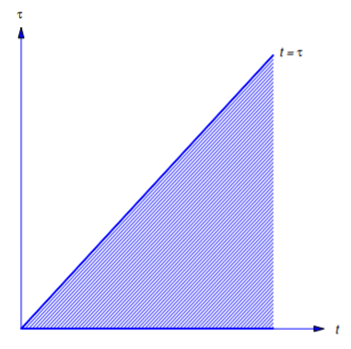
This iterated integral equals a double integral over the region shown in Figure 8.6.1 . Reversing the order of integration yields

\[\label{eq:8.6.6} {\mathscr L}(f*g)=\int_0^\infty f(\tau)\int^\infty_\tau e^{-st}g(t-\tau)\, dt \,d\tau.\]

However, the substitution \(x=t-\tau\) shows that

\[\begin{align*} \int^\infty_\tau e^{-st}g(t-\tau)\,dt&=\int_0^\infty e^{-s(x+\tau)}g(x)\,dx\\[4pt] &= e^{-s\tau}\int_0^\infty e^{-sx}g(x)\,dx=e^{-s\tau}G(s).\end{align*}\nonumber \]

Substituting this into Equation \ref{eq:8.6.6} and noting that \(G(s)\) is independent of \(\tau\) yields

\[\begin{align*} {\mathscr L}(f\ast g)&= \int_0^\infty e^{-s\tau} f(\tau)G(s)\,d\tau\\[4pt] & =G(s)\int_0^\infty e^{-st}f(\tau)\,d\tau=F(s)G(s).\end{align*}\nonumber \]

Figure 8.6.1

Example 8.6.1

Let

\[f(t)=e^{at}\quad \text{and} \quad g(t)=e^{bt}\qquad (a\ne b).\nonumber \]

Verify that \({\mathscr L}(f\ast g)={\mathscr L}(f){\mathscr L}(g)\), as implied by the convolution theorem.

Solution

We first compute

\[\begin{aligned} (f\ast g) &= \int_{0}^{t}e^{a\tau }e^{b(t-\tau )}d\tau &=e^{bt}\int_{0}^{t}e^{(a-b)\tau }d\tau \\ &= \left. e^{bt}\frac{e^{a-b}\tau }{a-b} \right|_{0}^{t} &=\frac{e^{bt}[e^{(a-b)t}-1] }{a-b} \\ &=\frac{e^{at}-e^{bt}}{a-b} \end{aligned}\nonumber \]

Since

\[e^{at}\leftrightarrow {1\over s-a}\quad\mbox{ and }\quad e^{bt}\leftrightarrow {1\over s-b},\nonumber \]

it follows that

\[\begin{aligned} {\mathscr L}(f\ast g)&={1\over a-b}\left[{1\over s-a}-{1\over s-b}\right]\\[5pt] &={1\over(s-a)(s-b)}\\[5pt] &={\mathscr L}(e^{at}){\mathscr L}(e^{bt})={\mathscr L}(f){\mathscr L}(g).\end{aligned}\nonumber \]

A Formula for the Solution of an Initial Value Problem

The convolution theorem provides a formula for the solution of an initial value problem for a linear constant coefficient second order equation with an unspecified. The next three examples illustrate this.

Example 8.6.2

Find a formula for the solution of the initial value problem

\[\label{eq:8.6.7} y''-2y'+y=f(t),\quad y(0)=k_0,\quad y'(0)=k_1.\]

Solution

Taking Laplace transforms in Equation \ref{eq:8.6.7} yields

\[(s^2-2s+1)Y(s)=F(s)+(k_1+k_0s)-2k_0.\nonumber \]

Therefore

\[\begin{align*} Y(s)&= {1\over(s-1)^2}F(s)+{k_1+k_0s-2k_0\over(s-1)^2}\\[5pt] &= {1\over(s-1)^2}F(s)+{k_0\over s-1}+{k_1-k_0\over(s-1)^2}.\end{align*}\nonumber \]

From the table of Laplace transforms,

\[{\mathscr L}^{-1}\left({k_0\over s-1}+{k_1-k_0\over(s-1)^2}\right) =e^t\left(k_0+(k_1-k_0)t\right). \nonumber\]

Since

\[{1\over(s-1)^2}\leftrightarrow te^t\quad \text{and} \quad F(s) \leftrightarrow f(t), \nonumber\]

the convolution theorem implies that

\[{\mathscr L}^{-1} \left({1\over(s-1)^2}F(s)\right)= \int_0^t\tau e^\tau f(t-\tau)\,d\tau. \nonumber\]

Therefore the solution of Equation \ref{eq:8.6.7} is

\[y(t)=e^t\left(k_0+(k_1-k_0)t\right)+\int_0^t\tau e^\tau f(t-\tau)\, d\tau. \nonumber\]

Example 8.6.3

Find a formula for the solution of the initial value problem

\[\label{eq:8.6.8} y''+4y=f(t),\quad y(0)=k_0,\quad y'(0)=k_1.\]

Solution

Taking Laplace transforms in Equation \ref{eq:8.6.8} yields

\[(s^2+4)Y(s) =F(s)+k_1+k_0s. \nonumber\]

Therefore

\[Y(s) ={1\over(s^2+4)}F(s)+{k_1+k_0s\over s^2+4}. \nonumber\]

From the table of Laplace transforms,

\[{\mathscr L}^{-1}\left(k_1+k_0s\over s^2+4\right)=k_0\cos 2t+{k_1\over 2}\sin 2t. \nonumber\]

Since

\[{1\over(s^2+4)}\leftrightarrow {1\over 2}\sin 2t\quad \text{and} \quad F(s)\leftrightarrow f(t), \nonumber\]

the convolution theorem implies that

\[{\mathscr L}^{-1}\left({1\over(s^2+4)}F(s)\right)= {1\over 2}\int_0^t f(t-\tau)\sin 2\tau\, d\tau. \nonumber \]

Therefore the solution of Equation \ref{eq:8.6.8} is

\[y(t)=k_0\cos 2t+{k_1\over 2}\sin 2t+{1\over 2}\int_0^tf(t-\tau)\sin 2\tau\,d\tau. \nonumber\]

Example 8.6.4

Find a formula for the solution of the initial value problem

\[\label{eq:8.6.9} y''+2y'+2y=f(t),\quad y(0)=k_0,\quad y'(0)=k_1.\]

Solution

Taking Laplace transforms in Equation \ref{eq:8.6.9} yields

\[(s^2+2s+2)Y(s)=F(s)+k_1+k_0s+2k_0.\nonumber \]

Therefore

\[\begin{aligned} Y(s)&=\frac{1}{(s+1)^{2}+1}F(s)+\frac{k_{1}+k_{0}s+2k_{0}}{(s+1)^{2}+1} \\ &=\frac{1}{(s+1)^{2}+1}F(s)+\frac{(k_{1}+k_{0})+k_{0}(s+1)}{(s+1)^{2}+1} \end{aligned} \nonumber \]

From the table of Laplace transforms,

\[{\mathscr L}^{-1}\left((k_1+k_0)+k_0(s+1)\over(s+1)^2+1\right)= e^{-t}\left((k_1+k_0)\sin t+k_0\cos t\right). \nonumber\]

Since

\[{1\over(s+1)^2+1}\leftrightarrow e^{-t}\sin t \quad \text{and} \quad F(s)\leftrightarrow f(t), \nonumber\]

the convolution theorem implies that

\[{\mathscr L}^{-1}\left({1\over(s+1)^2+1}F(s)\right)= \int_0^t f(t-\tau)e^{-\tau}\sin\tau \,d\tau. \nonumber\]

Therefore the solution of Equation \ref{eq:8.6.9} is

\[\label{eq:8.6.10} y(t)=e^{-t}\left((k_1+k_0)\sin t+k_0\cos t\right)+\int_0^tf(t-\tau)e^{-\tau}\sin\tau\,d\tau.\]

Evaluating Convolution Integrals

We’ll say that an integral of the form \(\displaystyle \int_0^t u(\tau)v(t-\tau)\,d\tau\) is a convolution integral. The convolution theorem provides a convenient way to evaluate convolution integrals.

Example 8.6.5

Evaluate the convolution integral

\[h(t)=\int_0^t(t-\tau)^5\tau^7 d\tau. \nonumber\]

Solution

We could evaluate this integral by expanding \((t-\tau)^5\) in powers of \(\tau\) and then integrating. However, the convolution theorem provides an easier way. The integral is the convolution of \(f(t)=t^5\) and \(g(t)=t^7\). Since

\[t^5\leftrightarrow {5!\over s^6}\quad\mbox{ and }\quad t^7 \leftrightarrow {7!\over s^8},\nonumber \]

the convolution theorem implies that

\[h(t)\leftrightarrow {5!7!\over s^{14}}={5!7!\over 13!}\, {13! \over s^{14}},\nonumber \]

where we have written the second equality because

\[{13!\over s^{14}}\leftrightarrow t^{13}.\nonumber \]

Hence,

\[h(t)={5!7!\over 13!}\, t^{13}.\nonumber \]

Example 8.6.6

Use the convolution theorem and a partial fraction expansion to evaluate the convolution integral

\[h(t)=\int_0^t\sin a(t-\tau)\cos b\tau\,d\tau\quad (|a|\ne |b|).\nonumber \]

Solution

Since

\[\sin at\leftrightarrow {a\over s^2+a^2}\quad\mbox{and}\quad \cos bt\leftrightarrow {s\over s^2+b^2},\nonumber \]

the convolution theorem implies that

\[H(s)={a\over s^2+a^2}{s\over s^2+b^2}.\nonumber \]

Expanding this in a partial fraction expansion yields

\[H(s)={a\over b^2-a^2}\left[{s\over s^2+a^2}-{s\over s^2+b^2}\right].\nonumber \]

Therefore

\[h(t)={a\over b^2-a^2}\left(\cos at-\cos bt\right).\nonumber \]

Volterra Integral Equations

An equation of the form

\[\label{eq:8.6.11} y(t)=f(t)+\int_0^t k(t-\tau) y(\tau)\,d\tau\]

is a Volterra integral equation. Here \(f\) and \(k\) are given functions and \(y\) is unknown. Since the integral on the right is a convolution integral, the convolution theorem provides a convenient formula for solving Equation \ref{eq:8.6.11}. Taking Laplace transforms in Equation \ref{eq:8.6.11} yields

\[Y(s)=F(s)+K(s) Y(s),\nonumber \]

and solving this for \(Y(s)\) yields

\[Y(s)={F(s)\over 1-K(s)}.\nonumber \]

We then obtain the solution of Equation \ref{eq:8.6.11} as \(y={\mathscr L}^{-1}(Y)\).

Example 8.6.7

Solve the integral equation

\[\label{eq:8.6.12} y(t)=1+2\int_0^t e^{-2(t-\tau)} y(\tau)\,d\tau.\]

Solution

Taking Laplace transforms in Equation \ref{eq:8.6.12} yields

\[Y(s)={1\over s}+{2\over s+2} Y(s),\nonumber \]

and solving this for \(Y(s)\) yields

\[Y(s)={1\over s}+{2\over s^2}.\nonumber \]

Hence,

\[y(t)=1+2t.\nonumber \]

Transfer Functions

The next theorem presents a formula for the solution of the general initial value problem

\[ay''+by'+cy=f(t),\quad y(0)=k_0,\quad y'(0)=k_1,\nonumber \]

where we assume for simplicity that \(f\) is continuous on \([0,\infty)\) and that \({\mathscr L}(f)\) exists. In Exercises 8.6.11-8.6.14 it is shown that the formula is valid under much weaker conditions on \(f\).

Theorem 8.6.3

Suppose \(f\) is continuous on \([0,\infty)\) and has a Laplace transform. Then the solution of the initial value problem

\[\label{eq:8.6.13} ay''+by'+cy=f(t),\quad y(0)=k_0,\quad y'(0)=k_1,\]

is

\[\label{eq:8.6.14} y(t)=k_0y_1(t)+k_1y_2(t)+\int_0^tw(\tau)f(t-\tau)\,d\tau,\]

where \(y_1\) and \(y_2\) satisfy

\[\label{eq:8.6.15} ay_1''+by_1'+cy_1=0,\quad y_1(0)=1,\quad y_1'(0)=0,\]

and

\[\label{eq:8.6.16} ay_2''+by_2'+cy_2=0,\quad y_2(0)=0,\quad y_2'(0)=1,\]

and

\[\label{eq:8.6.17} w(t)={1\over a}y_2(t).\]

Proof

Taking Laplace transforms in Equation \ref{eq:8.6.13} yields

\[p(s)Y(s)=F(s)+a(k_1+k_0s)+bk_0,\nonumber \]

where

\[p(s)=as^2+bs+c.\nonumber \]

Hence,

\[\label{eq:8.6.18} Y(s)=W(s)F(s)+V(s)\]

with

\[\label{eq:8.6.19} W(s)={1\over p(s)}\]

and

\[\label{eq:8.6.20} V(s)={a(k_1+k_0s)+bk_0\over p(s)}.\]

Taking Laplace transforms in Equation \ref{eq:8.6.15} and Equation \ref{eq:8.6.16} shows that

\[p(s)Y_1(s)=as+b\quad\mbox{and}\quad p(s)Y_2(s)=a.\nonumber \]

Therefore

\[Y_1(s)={as+b\over p(s)}\nonumber \]

and

\[\label{eq:8.6.21} Y_2(s)={a\over p(s)}.\]

Hence, Equation \ref{eq:8.6.20} can be rewritten as

\[V(s)=k_0Y_1(s)+k_1Y_2(s).\nonumber \]

Substituting this into Equation \ref{eq:8.6.18} yields

\[Y(s)=k_0Y_1(s)+k_1Y_2(s)+{1\over a}Y_2(s)F(s).\nonumber \]

Taking inverse transforms and invoking the convolution theorem yields Equation \ref{eq:8.6.14}. Finally, Equation \ref{eq:8.6.19} and Equation \ref{eq:8.6.21} imply Equation \ref{eq:8.6.17}.

It is useful to note from Equation \ref{eq:8.6.14} that \(y\) is of the form

\[y=v+h,\nonumber \]

where

\[v(t)=k_0y_1(t)+k_1y_2(t)\nonumber \]

depends on the initial conditions and is independent of the forcing function, while

\[h(t)=\int_0^tw(\tau)f(t-\tau)\, d\tau\nonumber \]

depends on the forcing function and is independent of the initial conditions. If the zeros of the characteristic polynomial

\[p(s)=as^2+bs+c\nonumber \]

of the complementary equation have negative real parts, then \(y_1\) and \(y_2\) both approach zero as \(t\to\infty\), so \(\lim_{t\to\infty}v(t)=0\) for any choice of initial conditions. Moreover, the value of \(h(t)\) is essentially independent of the values of \(f(t-\tau)\) for large \(\tau\), since \(\lim_{\tau\to\infty}w(\tau)=0\). In this case we say that \(v\) and \(h\) are transient and steady state components, respectively, of the solution \(y\) of Equation \ref{eq:8.6.13}. These definitions apply to the initial value problem of Example 8.6.4 , where the zeros of

\[p(s)=s^2+2s+2=(s+1)^2+1\nonumber \]

are \(-1\pm i\). From Equation \ref{eq:8.6.10}, we see that the solution of the general initial value problem of Example 8.6.4 is \(y=v+h\), where

\[v(t)=e^{-t}\left((k_1+k_0)\sin t+k_0\cos t\right)\nonumber \]

is the transient component of the solution and

\[h(t)=\int_0^t f(t-\tau)e^{-\tau}\sin\tau\,d\tau\nonumber \]

is the steady state component. The definitions don’t apply to the initial value problems considered in Examples 8.6.2 and 8.6.3 , since the zeros of the characteristic polynomials in these two examples don’t have negative real parts.

In physical applications where the input \(f\) and the output \(y\) of a device are related by Equation \ref{eq:8.6.13}, the zeros of the characteristic polynomial usually do have negative real parts. Then \(W={\mathscr L}(w)\) is called the transfer function of the device. Since

\[H(s)=W(s)F(s),\nonumber \]

we see that

\[W(s)={H(s)\over F(s)}\nonumber \]

is the ratio of the transform of the steady state output to the transform of the input.

Because of the form of

\[h(t)=\int_0^tw(\tau)f(t-\tau)\,d\tau,\nonumber \]

\(w\) is sometimes called the weighting function of the device, since it assigns weights to past values of the input \(f\). It is also called the impulse response of the device, for reasons discussed in the next section.

Formula Equation \ref{eq:8.6.14} is given in more detail in Exercises 8.6.8-8.6.10 for the three possible cases where the zeros of \(p(s)\) are real and distinct, real and repeated, or complex conjugates, respectively.