3E: Exercises
This page is a draft and is under active development.
( \newcommand{\kernel}{\mathrm{null}\,}\)
Chapter Review Exercises
Exercise 1
Let f(x+y)=f(x)+f(y)+x2y+xy2 and limx→0f(x)x=1. Then find f′(x).
- Answer
-
1+x2
Exercise 2
Use the limit definition of the derivative to find f′(x), where f(x)=3x2.
(You may use differentiation rules to check your answer). Find the tangent line to f(x)=3x2 at x=1.
- Answer
-
Under Construction
Exercise 3
Using the definition of the derivative (Newton's quotient)
find f′(x) for
f(x)=1√2x+5
- Answer
-
Under Construction
Exercise 4
Use the limit denition of the derivative to find f′(x), where f(x)=1x+1
(You may using differentiation rules to check your answer). Then find the equation of
the tangent line to f(x) at x=2
- Answer
-
Under Construction
Exercise 5
Find the derivatives of the following functions:
1) f(x)=√(x2+x+1)+x2
2) g(x)=cosxx+sinx
3) h(t)=t2+csct++sec2t
4) y(x)=3x2+52x2+x−3
5) f(x)=(x2+1)cotx3−cosxcscx
6) h(t)=√tan(2t−1)
7) y(x)=xx2−1
8) f(x)=ln(x2+1)x2
9) f(x)=(x−52x+1)3
10) h(t)=sin2(√tan(2t−1))
11) h(t)=sin(t)t
12) y=csc(cot(√4x))
13) y(x)=(x+5)7(x2−1)
14) g(x)=tan(2x)+√xcos(x)+x2
15) g(x)=cos(x)−√xtan(x)+3x2
16) y=3x+4x2+5$
17) y=sec(x)tan(x)
18) y=√5+√6x.
19) y=x3cos(x).
20) f(x)−tan(2x)2x+1
- Answer
-
Under Construction
Exercise 6
Find equations of the tangent and normal to \[y= \frac{2}{3-4 \sqrt{x}}\[ at the point (1,−2).
- Answer
-
Under Construction
Exercise 7
An object is released from rest (its initial velocity is zero) from the Empire State Building at a height of 1250 ft above street level. The height of the object can
be modeled by the position functions s=f(t)=1250−16t2.
a. Verify the object is still falling at t=5s:
b. Find the object's instantaneous velocity at the time t=5s
- Answer
-
Under Construction
Exercise 8
True or False? Justify the answer with a proof or a counterexample.
1) Every function has a derivative.
2) A continuous function has a continuous derivative.
3) A continuous function has a derivative.
4) If a function is differentiable, it is continuous.
- Answers to odd numbered questions
-
1. False.
3. False.
Exercise 9
Use the limit definition of the derivative to exactly evaluate the derivative:
1) f(x)=√x+4
2) f(x)=3x
- Answers to odd numbered questions
-
1. 12√x+4
Exercise 10
Find the derivatives of the following functions:
1) f(x)=3x3−4x2
2) f(x)=(4−x2)3
3) f(x)=esinx
4) f(x)=ln(x+2)
5) f(x)=x2cosx+xtan(x)
6) f(x)=√3x2+2
7) f(x)=x4sin−1(x)
8) x2y=(y+2)+xysin(x)
- Answers to odd numbered questions
-
1. 9x2+8x3
3. esinxcosx
5. xsec2(x)+2xcos(x)+tan(x)−x2sin(x)
7. 14(x√1−x2+sin−1(x))
Exercise 11
Find the following derivatives of various orders:
1) First derivative of y=xln(x)cosx
2) Third derivative of y=(3x+2)2
3) Second derivative of y=4x+x2sin(x)
- Answers to odd numbered questions
-
1. cosx⋅(lnx+1)−xln(x)sinx
3. 4x(ln4)2+2sinx+4xcosx−x2sinx
Exercise 12
Find the equation of the tangent line to the following equations at the specified point:
1) y=cos−1(x)+x at x=0
2) y=x+ex−1x at x=1
- Answer to even numbered questions
-
2. T=(2+e)x−2
Exercise 13
Draw the derivative for the following graphs.
21)
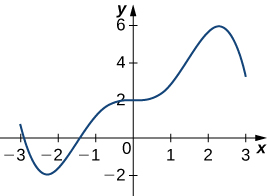
- Answer
-
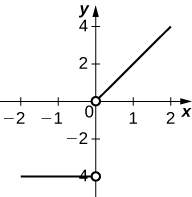
Exercise 14
The following questions concern the water level in Ocean City, New Jersey, in January, which can be approximated by w(t)=1.9+2.9cos(π6t), where t is measured in hours after midnight, and the height is measured in feet.
1) Find and graph the derivative. What is the physical meaning?
2) Find w′(3). What is the physical meaning of this value?
- Answers to even numbered questions
-
2. w′(3)=−2.9π6. At 3 a.m. the tide is decreasing at a rate of 1.514 ft/hr.
Exercise 15
The following questions consider the wind speeds of Hurricane Katrina, which affected New Orleans, Louisiana, in August 2005. The data are displayed in a table.
| Hours after Midnight, August 26 | Wind Speed (mph) |
| 1 | 45 |
| 5 | 75 |
| 11 | 100 |
| 29 | 115 |
| 49 | 145 |
| 58 | 175 |
| 73 | 155 |
| 81 | 125 |
| 85 | 95 |
| 107 | 35 |
Wind Speeds of Hurricane KatrinaSource: news.nationalgeographic.com/n..._timeline.html.
1) Using the table, estimate the derivative of the wind speed at hour 39. What is the physical meaning?
2) Estimate the derivative of the wind speed at hour 83. What is the physical meaning?
- Answers to even numbered questions
-
2. −7.5. The wind speed is decreasing at a rate of 7.5 mph/hr
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
Pamini Thangarajah (Mount Royal University, Calgary, Alberta, Canada)

