4.7: Applied Optimization Problems
- Page ID
- 13711
This page is a draft and is under active development.
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Set up and solve optimization problems in several applied fields.
In Section 3.3 we learned about extreme values -- the largest and smallest values a function attains on an interval. We motivated our interest in such values by discussing how it made sense to want to know the highest/lowest values of a stock or the fastest/slowest an object was moving. In this section, we apply the concepts of extreme values to solve "word problems," i.e., problems stated in terms of situations that require us to create the appropriate mathematical framework in which to solve the problem.
We start with a classic example which is followed by a discussion of the topic of optimization.
Solving Optimization Problems over a Closed, Bounded Interval
Example \(\PageIndex{1}\): Optimization: perimeter and area
A man has 100 feet of fencing, a large yard, and a small dog. He wants to create a rectangular enclosure for his dog with the fencing that provides the maximal area. What dimensions provide the maximal area?
Solution
One can likely guess the correct answer -- that is great. We will proceed to show how calculus can provide this answer in a context that proves this answer is correct.
It helps to make a sketch of the situation. Our enclosure is sketched twice in Figure \(\PageIndex{1}\), either with green grass and nice fence boards or as a simple rectangle. Either way, drawing a rectangle forces us to realize that we need to know the dimensions of this rectangle so we can create an area function -- after all, we are trying to maximize the area.
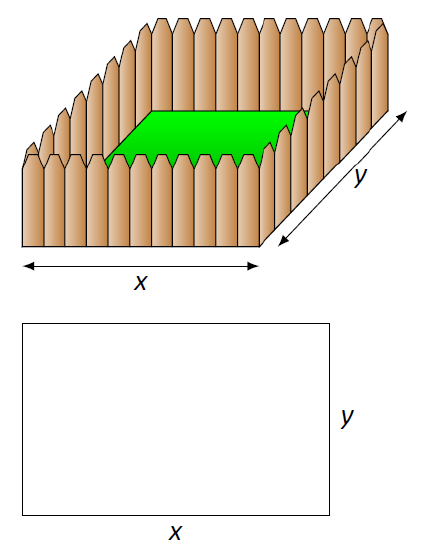
We let \(x\) and \(y\) denote the lengths of the sides of the rectangle. Clearly,
\[\text{Area}=xy.\]
We do not yet know how to handle functions with 2 variables; we need to reduce this down to a single variable. We know more about the situation: the man has 100 feet of fencing. By knowing the perimeter of the rectangle must be 100, we can create another equation:
\[\text{Perimeter} = 100 = 2x+2y.\]
We now have 2 equations and 2 unknowns. In the latter equation, we solve for \(y\):
\[y = 50-x.\]
Now substitute this expression for \(y\) in the area equation:
\[ \text{Area} = A(x) = x(50-x).\]
Note we now have an equation of one variable; we can truly call the Area a function of \(x\).
This function only makes sense when \(0\leq x \leq 50\), otherwise we get negative values of area. So we find the extreme values of \(A(x)\) on the interval \([0,50]\).
To find the critical points, we take the derivative of \(A(x)\) and set it equal to 0, then solve for \(x\).
\[\begin{align} A(x) &= x(50-x) \\ &= 50x-x^2 \\ A'(x) &= 50-2x \end{align}\]
We solve \(50-2x=0\) to find \(x=25\); this is the only critical point. We evaluate \(A(x)\) at the endpoints of our interval and at this critical point to find the extreme values; in this case, all we care about is the maximum.
Clearly \(A(0)=0\) and \(A(50)=0\), whereas \(A(25) = 625 \text{ft}^2\). This is the maximum. Since we earlier found \(y = 50-x\), we find that \(y\) is also \(25\). Thus the dimensions of the rectangular enclosure with perimeter of 100 ft. with maximum area is a square, with sides of length 25 ft.
This example is very simplistic and a bit contrived. (After all, most people create a design then buy fencing to meet their needs, and not buy fencing and plan later.) But it models well the necessary process: create equations that describe a situation, reduce an equation to a single variable, then find the needed extreme value.
"In real life," problems are much more complex. The equations are often not reducible to a single variable (hence multi--variable calculus is needed) and the equations themselves may be difficult to form. Understanding the principles here will provide a good foundation for the mathematics you will likely encounter later.
We outline here the basic process of solving these optimization problems.
Key Idea 6: Solving Optimization Problems
- Understand the problem. Clearly identify what quantity is to be maximized or minimized. Make a sketch if helpful.
- Create equations relevant to the context of the problem, using the information given. (One of these should describe the quantity to be optimized. We'll call this the fundamental equation.)
- If the fundamental equation defines the quantity to be optimized as a function of more than one variable, reduce it to a single variable function using substitutions derived from the other equations.
- Identify the domain of this function, keeping in mind the context of the problem.
- Find the extreme values of this function on the determined domain.
- Identify the values of all relevant quantities of the problem.
We will use Key Idea 6 in a variety of examples.
Example \(\PageIndex{2}\): Optimization: perimeter and area
Here is another classic calculus problem: A woman has a 100 feet of fencing, a small dog, and a large yard that contains a stream (that is mostly straight). She wants to create a rectangular enclosure with maximal area that uses the stream as one side. (Apparently, her dog won't swim away.) What dimensions provide the maximal area?
Solution
We will follow the steps outlined by Key Idea 6.
- We are maximizing area. A sketch of the region will help; Figure \(\PageIndex{2}\) gives two sketches of the proposed enclosed area. A key feature of the sketches is to acknowledge that one side is not fenced.
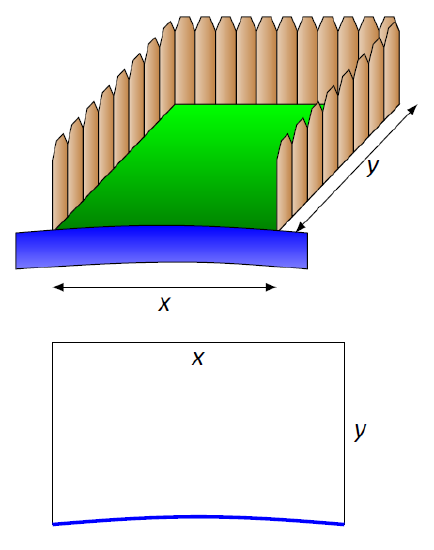
- We want to maximize the area; as in the example before, \[\text{Area} = xy.\] This is our fundamental equation. This defines area as a function of two variables, so we need another equation to reduce it to one variable.
We again appeal to the perimeter; here the perimeter is \[\text{Perimeter} = 100 = x+2y.\[ Note how this is different than in our previous example. - We now reduce the fundamental equation to a single variable. In the perimeter equation, solve for \(y\): \(y = 50 - x/2\). We can now write Area as \[\text{Area} = A(x) = x(50-x/2) = 50x - \frac12x^2.\] Area is now defined as a function of one variable.
- We want the area to be nonnegative. Since \(A(x) = x(50-x/2)\), we want \(x\geq 0\) and \(50-x/2\geq 0\). The latter inequality implies that \(x\leq100\), so \(0\leq x\leq 100\).
- We now find the extreme values. At the endpoints, the minimum is found, giving an area of 0.
Find the critical points. We have \(A'(x) = 50-x\); setting this equal to 0 and solving for \(x\) returns \(x=50\). This gives an area of \[A(50) = 50(25) = 1250.\[
| \(x\) | \(A(x)\) |
| 0 | 0 |
| 50 | (50)(25) |
| 100 | 0 |
- We earlier set \(y = 50-x/2\); thus \(y = 25\). Thus our rectangle will have two sides of length 25 and one side of length 50, with a total area of 1250 ft\(^2\).
Keep in mind as we do these problems that we are practicing a process; that is, we are learning to turn a situation into a system of equations. These equations allow us to write a certain quantity as a function of one variable, which we then optimize.
Example \(\PageIndex{3}\): Optimization: minimizing cost
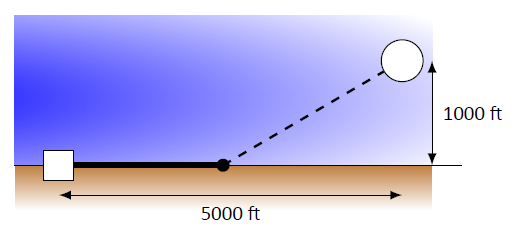
A power line needs to be run from a power station located on the beach to an offshore facility. Figure \(\PageIndex{3}\) shows the distances between the power station to the facility.
It costs $50/ft. to run a power line along the land, and $130/ft. to run a power line under water. How much of the power line should be run along the land to minimize the overall cost? What is the minimal cost?
Solution
We will follow the strategy of Key Idea 6 implicitly, without specifically numbering steps.
There are two immediate solutions that we could consider, each of which we will reject through "common sense." First, we could minimize the distance by directly connecting the two locations with a straight line. However, this requires that all the wire be laid underwater, the most costly option. Second, we could minimize the underwater length by running a wire all 5000 ft. along the beach, directly across from the offshore facility. This has the undesired effect of having the longest distance of all, probably ensuring a non--minimal cost.
The optimal solution likely has the line being run along the ground for a while, then underwater, as the figure implies. We need to label our unknown distances -- the distance run along the ground and the distance run underwater. Recognizing that the underwater distance can be measured as the hypotenuse of a right triangle, we choose to label the distances as shown in Figure \(\PageIndex{4}\).
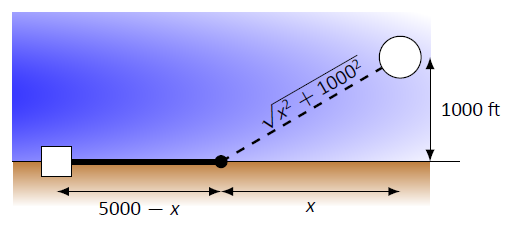
By choosing \(x\) as we did, we make the expression under the square root simple. We now create the cost function.
\[
\begin{array}{ccccc}
\text{Cost} &=& \text{land cost} &+ & \text{water cost} \\
& & \text{\$50}\times \text{land distance} &+& \text{\$130}\times \text{water distance} \\
& & 50(5000-x) &+& 130\sqrt{x^2+1000^2}.\\
\end{array}
\]
So we have \(c(x) = 50(5000-x)+ 130\sqrt{x^2+1000^2}\). This function only makes sense on the interval \([0,5000]\). While we are fairly certain the endpoints will not give a minimal cost, we still evaluate \(c(x)\) at each to verify.
\[c(0) = 380,000 \quad\quad c(5000) \approx 662,873.\]
We now find the critical values of \(c(x)\). We compute \(c'(x)\) as
\[c'(x) = -50+\frac{130x}{\sqrt{x^2+1000^2}}.\]
Recognize that this is never undefined. Setting \(c'(x)=0\) and solving for \(x\), we have:
\[ \begin{align} -50+\frac{130x}{\sqrt{x^2+1000^2}} &= 0 \\ \frac{130x}{\sqrt{x^2+1000^2}} &= 50\\ \frac{130^2x^2}{x^2+1000^2} &= 50^2\\ 130^2x^2 &= 50^2(x^2+1000^2) \\ 130^2x^2-50^2x^2 &= 50^2\cdot1000^2\\ (130^2-50^2)x^2 &= 50,000^2\\ x^2 &= \frac{50,000^2}{130^2-50^2}\\ x &= \frac{50,000}{\sqrt{130^2-50^2}}\\ x & = \frac{50,000}{120} =416\frac23\approx 416.67. \end{align}\]
Evaluating \(c(x)\) at \(x=416.67\) gives a cost of about $370,000. The distance the power line is laid along land is \(5000-416.67 = 4583.33\) ft., and the underwater distance is \(\sqrt{416.67^2+1000^2} \approx 1083\) ft.
Example \(\PageIndex{4}\): Maximizing the Volume of a Box
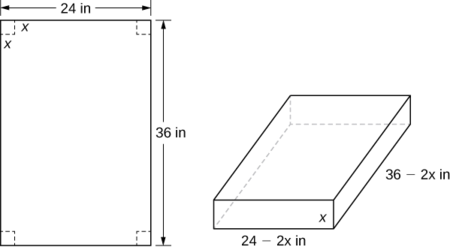
An open-top box is to be made from a \(24\) in. by \(36\) in. the piece of cardboard by removing a square from each corner of the box and folding up the flaps on each side. What size square should be cut out of each corner to get a box with the maximum volume?
Solution
Step 1: Let \(x\) be the side length of the square to be removed from each corner (Figure \(\PageIndex{3}\)). Then, the remaining four flaps can be folded up to form an open-top box. Let \(V\) be the volume of the resulting box.
Step 2: We are trying to maximize the volume of a box. Therefore, the problem is to maximize \(V\).
Step 3: As mentioned in step \(2\), are trying to maximize the volume of a box. The volume of a box is
\[V=L⋅W⋅H \nonumber,\]
where \(L,W,\)and \(H\) are the length, width, and height, respectively.
Step 4: From Figure \(\PageIndex{3}\), we see that the height of the box is \(x\) inches, the length is \(36−2x\) inches, and the width is \(24−2x\) inches. Therefore, the volume of the box is
\[ \begin{align*} V(x) &=(36−2x)(24−2x)x \\[5pt] &=4x^3−120x^2+864x \end{align*}.\]
Step 5: To determine the domain of consideration, let’s examine Figure \(\PageIndex{3}\). Certainly, we need \(x>0.\) Furthermore, the side length of the square cannot be greater than or equal to half the length of the shorter side, \(24\) in.; otherwise, one of the flaps would be completely cut off. Therefore, we are trying to determine whether there is a maximum volume of the box for \(x\) over the open interval \((0,12).\) Since \(V\) is a continuous function over the closed interval \([0,12]\), we know \(V\) will have an absolute maximum over the closed interval. Therefore, we consider \(V\) over the closed interval \([0,12]\) and check whether the absolute maximum occurs at an interior point.
Step 6: Since \(V(x)\) is a continuous function over the closed, bounded interval \([0,12], V\) must have an absolute maximum (and an absolute minimum). Since \(V(x)=0\) at the endpoints and \(V(x)>0\) for \(0<x<12,\) the maximum must occur at a critical point. The derivative is
\(V′(x)=12x^2−240x+864.\)
To find the critical points, we need to solve the equation
\(12x^2−240x+864=0.\)
Dividing both sides of this equation by \(12\), the problem simplifies to solving the equation
\(x^2−20x+72=0.\)
Using the quadratic formula, we find that the critical points are
\[\begin{align*} x&=\dfrac{20±\sqrt{(−20)^2−4(1)(72)}}{2} \\[5pt] &=\dfrac{20±\sqrt{112}}{2} \\[5pt] &=\dfrac{20±4\sqrt{7}}{2} \\[5pt] &=10±2\sqrt{7} \end{align*}.\]
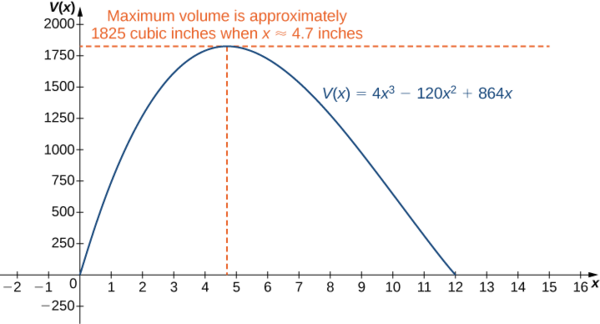
Since \(10+2\sqrt{7}\) is not in the domain of consideration, the only critical point we need to consider is \(10−2\sqrt{7}\). Therefore, the volume is maximized if we let \(x=10−2\sqrt{7}\, in.\) The maximum volume is
\[V(10−2\sqrt{7})=640+448\sqrt{7}≈1825\,in.^3 \nonumber \]
as shown in the following graph.
Watch a video about optimizing the volume of a box.
Exercise \(\PageIndex{2}\)
Suppose the dimensions of the cardboard in Example \(\PageIndex{2}\) are 20 in. by 30 in. Let \(x\) be the side length of each square and write the volume of the open-top box as a function of \(x\). Determine the domain of consideration for \(x\).
- Hint
-
The volume of the box is \(L⋅W⋅H.\)
- Answer
-
\(V(x)=x(20−2x)(30−2x).\) The domain is \([0,10]\).
Example \(\PageIndex{5}\): Minimizing Travel Time
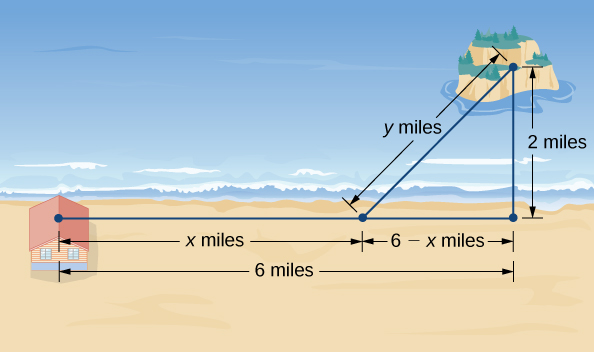
An island is \(2\,mi\) due north of its closest point along a straight shoreline. A visitor is staying at a cabin on the shore that is \(6\,mi\) west of that point. The visitor is planning to go from the cabin to the island. Suppose the visitor runs at a rate of \(8\,mph\) and swims at a rate of \(3\,mph\). How far should the visitor run before swimming to minimize the time it takes to reach the island?
Solution
Step 1: Let \(x\) be the distance running and let \(y\) be the distance swimming (Figure \(\PageIndex{5}\)). Let \(T\) be the time it takes to get from the cabin to the island.
Step 2: The problem is to minimize \(T\).
Step 3: To find the time spent traveling from the cabin to the island, add the time spent running and the time spent swimming. Since Distance = Rate × Time \((D=R×T),\) the time spent running is
\(T_{running}=\dfrac{D_{running}}{R_{running}}=\dfrac{x}{8}\),
and the time spent swimming is
\(T_{swimming}=\dfrac{D_{swimming}}{R_{swimming}}=\dfrac{y}{3}\).
Therefore, the total time spent traveling is
\(T=\dfrac{x}{8}+\dfrac{y}{3}\).
Step 4: From Figure \(\PageIndex{5}\), the line segment of \(y\) miles forms the hypotenuse of a right triangle with legs of length \(2mi\) and \(6−xmi\). Therefore, by the Pythagorean theorem, \(2^2+(6−x)^2=y^2\), and we obtain \(y=\sqrt{(6−x)^2+4}\). Thus, the total time spent traveling is given by the function
\(T(x)=\dfrac{x}{8}+\dfrac{\sqrt{(6−x)^2+4}}{3}\).
Step 5: From Figure \(\PageIndex{5}\), we see that \(0≤x≤6\). Therefore, \([0,6]\) is the domain of consideration.
Step 6: Since \(T(x)\) is a continuous function over a closed, bounded interval, it has a maximum and a minimum. Let’s begin by looking for any critical points of \(T\) over the interval \([0,6].\) The derivative is
\[\begin{align*} T′(x) &=\dfrac{1}{8}−\dfrac{1}{2}\dfrac{[(6−x)^2+4]^{−1/2}}{3}⋅2(6−x) \\[5pt] &=\dfrac{1}{8}−\dfrac{(6−x)}{3\sqrt{(6−x)^2+4}} \end{align*}\]
If \(T′(x)=0,\), then
\[\dfrac{1}{8}=\dfrac{6−x}{3\sqrt{(6−x)^2+4}} \nonumber\]
Therefore,
\[3\sqrt{(6−x)^2+4}=8(6−x). \nonumber\]
Squaring both sides of this equation, we see that if \(x\) satisfies this equation, then \(x\) must satisfy
\[9[(6−x)^2+4]=64(6−x)^2,\nonumber \]
which implies
\[55(6−x)^2=36. \nonumber\]
We conclude that if \(x\) is a critical point, then \(x\) satisfies
\[(x−6)^2=\dfrac{36}{55}. \nonumber\]
Therefore, the possibilities for critical points are
\[(x=6±\dfrac{6}{\sqrt{55}}.\nonumber\]
Since \(x=6+6/\sqrt{55}\) is not in the domain, it is not a possibility for a critical point. On the other hand, \(x=6−6/\sqrt{55}\) is in the domain. Since we squared both sides of Equation to arrive at the possible critical points, it remains to verify that \(x=6−6/\sqrt{55}\) satisfies Equation. Since \(x=6−6/\sqrt{55}\) does satisfy that equation, we conclude that \(x=6−6/\sqrt{55}\) is a critical point, and it is the only one. To justify that the time is minimized for this value of x, we just need to check the values of \(T(x)\) at the endpoints \(x=0\) and \(x=6\), and compare them with the value of \(T(x)\) at the critical point \(x=6−6/\sqrt{55}\). We find that \(T(0)≈2.108h\) and \(T(6)≈1.417h\), whereas
\[T(6−6/\sqrt{55})≈1.368h. \nonumber\]
Therefore, we conclude that \(T\) has a local minimum at \(x≈5.19 mi\).
Exercise \(\PageIndex{3}\)
Suppose the island is \(1\, mi\) from shore, and the distance from the cabin to the point on the shore closest to the island is \(15\,mi\). Suppose a visitor swims at the rate of \(2.5\,mph\) and runs at a rate of \(6\,mph\). Let \(x\) denote the distance the visitor will run before swimming, and find a function for the time it takes the visitor to get from the cabin to the island.
- Hint
-
The time \(T=T_{running}+T_{swimming}.\)
- Answer
-
\[T(x)=\dfrac{x}{6}+\dfrac{\sqrt{(15−x)^2+1}}{2.5} \nonumber \]
In business, companies are interested in maximizing revenue. In the following example, we consider a scenario in which a company has collected data on how many cars it is able to lease, depending on the price it charges its customers to rent a car. Let’s use these data to determine the price the company should charge to maximize the amount of money it brings in.
Example \(\PageIndex{6}\): Maximizing Revenue
Owners of a car rental company have determined that if they charge customers \(p\) dollars per day to rent a car, where \(50≤p≤200\), the number of cars \(n\) they rent per day can be modeled by the linear function \(n(p)=1000−5p\). If they charge \($50\) per day or less, they will rent all their cars. If they charge \($200\) per day or more, they will not rent any cars. Assuming the owners plan to charge customers between \($50\) per day and \($200\) per day to rent a car, how much should they charge to maximize their revenue?
Solution
Step 1: Let \(p\) be the price charged per car per day and let n be the number of cars rented per day. Let \(R\) be the revenue per day.
Step 2: The problem is to maximize \(R.\)
Step 3: The revenue (per day) is equal to the number of cars rented per day times the price charged per car per day—that is, \(R=n×p.\)
Step 4: Since the number of cars rented per day is modeled by the linear function \(n(p)=1000−5p,\) the revenue \(R\) can be represented by the function
\[ \begin{align*} R(p) &=n×p \\[5pt] &=(1000−5p)p \\[5pt] &=−5p^2+1000p.\end{align*}\]
Step 5: Since the owners plan to charge between \($50\) per car per day and \($200\) per car per day, the problem is to find the maximum revenue \(R(p)\) for \(p\) in the closed interval \([50,200]\).
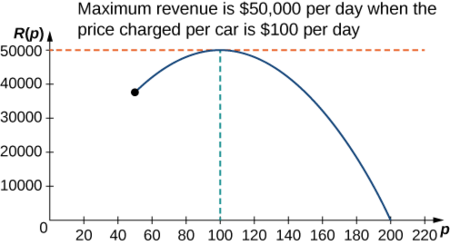
Step 6: Since \(R\) is a continuous function over the closed, bounded interval \([50,200]\), it has an absolute maximum (and an absolute minimum) in that interval. To find the maximum value, look for critical points. The derivative is \(R′(p)=−10p+1000.\) Therefore, the critical point is \(p=100\) When \(p=100, R(100)=$50,000.\) When \(p=50, R(p)=$37,500\). When \(p=200, R(p)=$0\).
Therefore, the absolute maximum occurs at \(p=$100\). The car rental company should charge \($100\) per day per car to maximize revenue as shown in the following figure.
Exercise \(\PageIndex{4}\)
A car rental company charges its customers \(p\) dollars per day, where \(60≤p≤150\). It has found that the number of cars rented per day can be modeled by the linear function \(n(p)=750−5p.\) How much should the company charge each customer to maximize revenue?
- Hint
-
\(R(p)=n×p,\) where \(n\) is the number of cars rented and \(p\) is the price charged per car.
- Answer
-
The company should charge \($75\) per car per day.
Example \(\PageIndex{7}\): Maximizing the Area of an Inscribed Rectangle
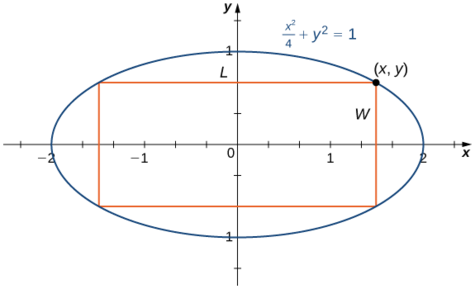
A rectangle is to be inscribed in the ellipse
\[\dfrac{x^2}{4}+y^2=1. \nonumber \]
What should the dimensions of the rectangle be to maximize its area? What is the maximum area?
Solution
Step 1: For a rectangle to be inscribed in the ellipse, the sides of the rectangle must be parallel to the axes. Let \(L\) be the length of the rectangle and \(W\) be its width. Let \(A\) be the area of the rectangle.
Step 2: The problem is to maximize \(A\).
Step 3: The area of the rectangle is \(A=LW.\)
Step 4: Let \((x,y)\) be the corner of the rectangle that lies in the first quadrant, as shown in Figure \(\PageIndex{7}\). We can write length \(L=2x\) and width \(W=2y\). Since \(\dfrac{x^2}{4+y^2=1}\) and \(y>0\), we have \(y=\sqrt{\dfrac{1−x^2}{4}}\). Therefore, the area is
\(A=LW=(2x)(2y)=4x\sqrt{\dfrac{1−x^2}{4}}=2x\sqrt{4−x^2}\)
Step 5: From Figure \(\PageIndex{7}\), we see that to inscribe a rectangle in the ellipse, the \(x\)-coordinate of the corner in the first quadrant must satisfy \(0<x<2\). Therefore, the problem reduces to looking for the maximum value of \(A(x)\) over the open interval \((0,2)\). Since \(A(x)\) will have an absolute maximum (and absolute minimum) over the closed interval \([0,2]\), we consider \(A(x)=2x\sqrt{4−x^2}\) over the interval \([0,2]\). If the absolute maximum occurs at an interior point, then we have found an absolute maximum in the open interval.
Step 6: As mentioned earlier, \(A(x)\) is a continuous function over the closed, bounded interval \([0,2]\). Therefore, it has an absolute maximum (and absolute minimum). At the endpoints \(x=0\) and \(x=2, A(x)=0.\) For \(0<x<2, A(x)>0\).
Therefore, the maximum must occur at a critical point. Taking the derivative of \(A(x)\), we obtain
\[ \begin{align*} A'(x) &=2\sqrt{4−x^2}+2x⋅\dfrac{1}{2\sqrt{4−x^2}}(−2x) \\[5pt] &=2\sqrt{4−x^2}−\dfrac{2x^2}{\sqrt{4−x^2}} \\[5pt] &=\dfrac{8−4x^2}{\sqrt{4−x^2}} . \end{align*}\]
To find critical points, we need to find where \(A'(x)=0.\) We can see that if \(x\) is a solution of
\(\dfrac{8−4x^2}{\sqrt{4−x^2}}=0\),
then \(x\) must satisfy
\[8−4x^2=0. \label{eq5a}\]
Therefore, \(x^2=2.\) Thus, \(x=±\sqrt{2}\) are the possible solutions of Equation. Since we are considering \(x\) over the interval \([0,2]\), \(x=\sqrt{2}\) is a possibility for a critical point, but \(x=−\sqrt{2}\) is not. Therefore, we check whether \(\sqrt{2}\) is a solution of Equation. Since \(x=\sqrt{2}\) is a solution of Equation \ref{eq5a}, we conclude that \(\sqrt{2}\) is the only critical point of \(A(x)\) in the interval \([0,2]\).
Therefore, \(A(x)\) must have an absolute maximum at the critical point \(x=\sqrt{2}\). To determine the dimensions of the rectangle, we need to find the length \(L\) and the width \(W\). If \(x=\sqrt{2}\) then
\[y=\sqrt{1−\dfrac{(\sqrt{2})^2}{4}}=\sqrt{1−\dfrac{1}{2}}=\dfrac{1}{\sqrt{2}}.\]
Therefore, the dimensions of the rectangle are \(L=2x=2\sqrt{2}\) and \(W=2y=\dfrac{2}{\sqrt{2}}=\sqrt{2}\). The area of this rectangle is\( A=LW=(2\sqrt{2})(\sqrt{2})=4.\)
Exercise \(\PageIndex{5}\)
Modify the area function \(A\) if the rectangle is to be inscribed in the unit circle \(x^2+y2^=1\). What is the domain of consideration?
- Hint
-
If \((x,y)\) is the vertex of the square that lies in the first quadrant, then the area of the square is \(A=(2x)(2y)=4xy.\)
- Answer
-
\(A(x)=4x\sqrt{1−x^2}.\) The domain of consideration is \([0,1]\).
Solving Optimization Problems when the Interval Is Not Closed or Is Unbounded
In the previous examples, we considered functions on closed, bounded domains. Consequently, by the extreme value theorem, we were guaranteed that the functions had absolute extrema. Let’s now consider functions for which the domain is neither closed nor bounded.
Many functions still have at least one absolute extrema, even if the domain is not closed or the domain is unbounded. For example, the function \(f(x)=x^2+4\) over \((−∞,∞)\) has an absolute minimum of \(4\) at \(x=0\). Therefore, we can still consider functions over unbounded domains or open intervals and determine whether they have any absolute extrema. In the next example, we try to minimize a function over an unbounded domain. We will see that, although the domain of consideration is \((0,∞),\) the function has an absolute minimum.
In the following example, we look at constructing a box of least surface area with a prescribed volume. It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the smallest surface area. Consequently, we consider the modified problem of determining which open-topped box with a specified volume has the smallest surface area.
Example \(\PageIndex{8}\): Minimizing Surface Area
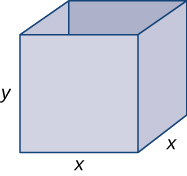
A rectangular box with a square base, an open top, and a volume of \(216 in.^3\) is to be constructed. What should the dimensions of the box be to minimize the surface area of the box? What is the minimum surface area?
Solution
Step 1: Draw a rectangular box and introduce the variable \(x\) to represent the length of each side of the square base; let \(y\) represent the height of the box. Let \(S\) denote the surface area of the open-top box.
Step 2: We need to minimize the surface area. Therefore, we need to minimize \(S\).
Step 3: Since the box has an open top, we need only determine the area of the four vertical sides and the base. The area of each of the four vertical sides is \(x⋅y.\) The area of the base is \(x^2\). Therefore, the surface area of the box is
\(S=4xy+x^2\).
Step 4: Since the volume of this box is \(x^2y\) and the volume is given as \(216in.^3\), the constraint equation is
\(x^2y=216\).
Solving the constraint equation for \(y\), we have \(y=\dfrac{216}{x^2}\). Therefore, we can write the surface area as a function of \(x\) only:
\[S(x)=4x(\dfrac{216}{x^2})+x^2.\]
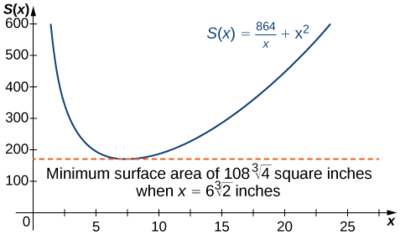
Therefore, \(S(x)=\dfrac{864}{x}+x^2\).
Step 5: Since we are requiring that \(x^2y=216\), we cannot have \(x=0\). Therefore, we need \(x>0\). On the other hand, \(x\) is allowed to have any positive value. Note that as \(x\) becomes large, the height of the box \(y\) becomes correspondingly small so that \(x^2y=216\). Similarly, as \(x\) becomes small, the height of the box becomes correspondingly large. We conclude that the domain is the open, unbounded interval \((0,∞)\). Note that, unlike the previous examples, we cannot reduce our problem to looking for an absolute maximum or absolute minimum over a closed, bounded interval. However, in the next step, we discover why this function must have an absolute minimum over the interval \((0,∞).\)
Step 6: Note that as \(x→0+^,S(x)→∞.\) Also, as \(x→∞, S(x)→∞\). Since \(S\) is a continuous function that approaches infinity at the ends, it must have an absolute minimum at some \(x∈(0,∞)\). This minimum must occur at a critical point of \(S\). The derivative is
\[S′(x)=−\dfrac{864}{x^2}+2x.\]
Therefore, \(S′(x)=0\) when \(2x=\dfrac{864}{x^2}\). Solving this equation for \(x\), we obtain \(x^3=432\), so \(x=\sqrt[3]{432}=6\sqrt[3]{2}.\) Since this is the only critical point of \(S\), the absolute minimum must occur at \(x=6\sqrt[3]{2}\) (see Figure \(\PageIndex{9}\)).
When \(x=6\sqrt[3]{2}\), \(y=\dfrac{216}{(6\sqrt[3]{2})^2}=3\sqrt[3]{2}in\). Therefore, the dimensions of the box should be \(x=6\sqrt[3]{2}in.\) and \(y=3\sqrt[3]{2}in.\) With these dimensions, the surface area is
\[S(6\sqrt[3]{2})=\dfrac{864}{6\sqrt[3]{2}}+(6\sqrt[3]{2})^2=108\sqrt[3]{4}in.^2\]
Exercise \(\PageIndex{8}\)
Consider the same open-top box, which is to have volume \(216in.^3\). Suppose the cost of the material for the base is \(20¢/in.^2\) and the cost of the material for the sides is \(30¢/in.^2\) and we are trying to minimize the cost of this box. Write the cost as a function of the side lengths of the base. (Let \(x\) be the side length of the base and \(y\) be the height of the box.)
- Hint
-
If the cost of one of the sides is \(30¢/in.^2,\) the cost of that side is \(0.30xy.\)
- Answer
-
\(c(x)=\dfrac{259.2}{x}+0.2x^2\) dollars
Example \(\PageIndex{9}\): Minimizing Cost
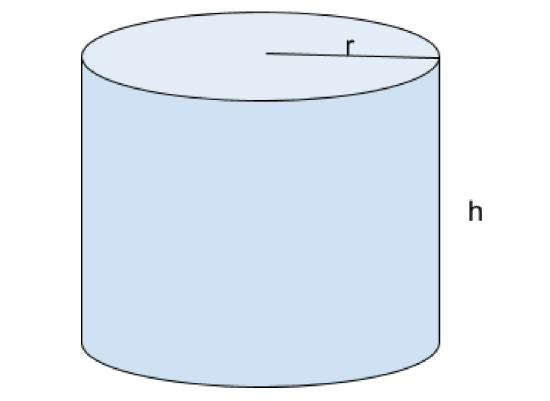
An open-topped cylindrical can is to have volume \(300\, cm^3\). The material for the bottom of the can costs \(10\, cents/cm^2\), for its curved side costs \(5 \, cents/cm^2.\) Find the dimensions of the can that minimize the cost of the can.
Solution
Step 1: Draw a cylindrical can and introduce the variable \(r\) to represent the radius of the circular base; let \(h\) represent the height of the can. Let \(C\) denote the cost to produce a can.
Step 2: Given: Volume of the can \(V= 300\). We need to minimize the cost. Therefore, we need to minimize \(C\).
Step 3: Since the can has an open top, we need only determine the cost to produce the bottom and the cost to produce the side.
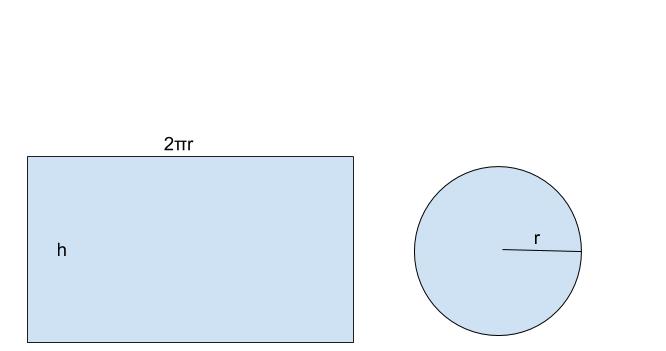.jpg?revision=1&size=bestfit&width=666&height=351)
The surface area of the curved side is \(2 \pi rh\) The area of the bottom is \(\pi r^2\). Therefore, the cost to produce the can is
\(C=(5) 2 \pi rh+ (10)\pi r^2\), with \(r \geq 0\).
Step 4: Since the volume of this can \( \pi r^2 h\) and the volume is given as \(300 \), the constraint equation is
\(\pi r^2 h=300\).
Solving the constraint equation for \(h\), we have \(h=\dfrac{300}{\pi r^2}\). Therefore, we can write the cost as a function of \ (r\) only:
\(C=(5) 2 \pi r\dfrac{300}{\pi r^2}+ (10)\pi r^2\).
Therefore, \(C=\dfrac{3000 }{ r}+ (10)\pi r^2\).
Step 5: Since we are requiring that \(\pi r^2 h=300\), we cannot have \(r=0\). Therefore, we need \(r>0\). On the other hand, \(r\) is allowed to have any positive value. Note that as \(r\) becomes large, the height of the can \(h\) becomes correspondingly small so that \(\pi r^2 h=300\). Similarly, as \(r\) becomes small, the height of the can becomes correspondingly large. We conclude that the domain is the open, unbounded interval \((0,∞)\). In the next step, we discover why this function must have an absolute minimum over the interval \((0,∞).\)
Step 6: Note that as \(x→0+^, C(r)→∞.\) Also, as \(r→∞, C(r)→∞\). Since \(C\) is a continuous function that approaches infinity at the ends, it must have an absolute minimum at some \(r∈(0,∞)\). This minimum must occur at a critical point of \(C\). The derivative is
\[C′(x)=−\dfrac{3000}{r^2}+2r.\]
Therefore, \(C′(r)=0\) when \(2r=\dfrac{3000}{r^2}\). Solving this equation for \(r\), we obtain \(r^3=1500\), so \(r=\sqrt[3]{1500}.\) Since this is the only critical point of \(C\), the absolute minimum must occur at \(r=\sqrt[3]{1500}\).
When \(r=\sqrt[3]{1500}\), \(h= \dfrac{300}{\pi {\sqrt[3]{1500}}^2}\). Therefore, the dimensions of the can sho uld be \(r=\sqrt[3]{1500}in.\) and \( h= \dfrac{300}{\pi {\sqrt[3]{1500}}^2}\).
With these dimensions, the cost is
Exercise \(\PageIndex{9}\)
Pop cans to hold \(300\) ml are made in the shape of right circular cylinders. Find the dimensions of the can that minimize the surface area.
- Answer
-
Add answer text here and it will automatically be hidden if you have a "AutoNum" template active on the page.
Example \(\PageIndex{10}\): Closest point
Find the point on the curve \(y=\frac{-x^2}{3}\) that is closest to the point \(P(4,-1).\)
In the exercises, you will see a variety of situations that require you to combine problem--solving skills with calculus. Focus on the process; learn how to form equations from situations that can be manipulated into what you need. Eschew memorizing how to do "this kind of problem" as opposed to "that kind of problem." Learning a process will benefit one far longer than memorizing a specific technique.
The next section introduces our final application of the derivative: differentials. Given \(y=f(x)\), they offer a method of approximating the change in \(y\) after \(x\) changes by a small amount.
Key Concepts
- To solve an optimization problem, begin by drawing a picture and introducing variables.
- Find an equation relating the variables.
- Find a function of one variable to describe the quantity that is to be minimized or maximized.
- Look for critical points to locate local extrema.
Glossary
- optimization problems
- problems that are solved by finding the maximum or minimum value of a function
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
Gregory Hartman (Virginia Military Institute). Contributions were made by Troy Siemers and Dimplekumar Chalishajar of VMI and Brian Heinold of Mount Saint Mary's University. This content is copyrighted by a Creative Commons Attribution - Noncommercial (BY-NC) License. http://www.apexcalculus.com/
Integrated by Justin Marshall.
Pamini Thangarajah (Mount Royal University, Calgary, Alberta, Canada)

