3.6E: Exercises
- Page ID
- 13713
This page is a draft and is under active development.
Exercise \(\PageIndex{1}\)
For the following exercises, answer by proof, counterexample, or explanation.
1) When you find the maximum for an optimization problem, why do you need to check the sign of the derivative around the critical points?
- Answer
-
The critical points can be the minima, maxima, or neither.
2) Why do you need to check the endpoints for optimization problems?
3) True or False. For every continuous nonlinear function, you can find the value xx that maximizes the function.
- Answer
-
False; \(y=−x^2\) has a minimum only
4) True or False. For every continuous nonconstant function on a closed, finite domain, there exists at least one xx that minimizes or maximizes the function
Exercise \(\PageIndex{2}\)
To carry a suitcase on an airplane, the length+width+height of the box must be less than or equal to 62in. Assuming the height is fixed, show that the maximum volume is \(V=h(31−(12)h)\)
What height allows you to have the largest volume?
- Answer
-
Under Construction
Exercise \(\PageIndex{3}\)
You are constructing a cardboard box with the dimensions 2m by 4m. You then cut equal-size squares from each corner so you may fold the edges. What are the dimensions of the box with the largest volume?
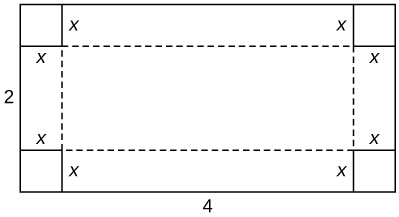
- Answer
-
Under Construction
Exercise \(\PageIndex{4}\)
Find the positive integer that minimizes the sum of the number and its reciprocal.
- Answer
-
11
Exercise \(\PageIndex{5}\)
For the following exercises, consider the construction of a pen to enclose an area.
1) You have 400ft of fencing to construct a rectangular pen for cattle. What are the dimensions of the pen that maximize the area?
- Answer
-
100ft x 100ft
2) You have 800ft of fencing to make a pen for hogs. If you have a river on one side of your property, what is the dimension of the rectangular pen that maximizes the area?
3) You need to construct a fence around an area of 1600ft. 1600ft. What are the dimensions of the rectangular pen to minimize the amount of material needed?
- Answer
-
40ft x 40ft
Exercise \(\PageIndex{6}\)
Two poles are connected by a wire that is also connected to the ground. The first pole is 20ft tall and the second pole is 10ft tall. There is a distance of 30ft between the two poles. Where should the wire be anchored to the ground to minimize the amount of wire needed?
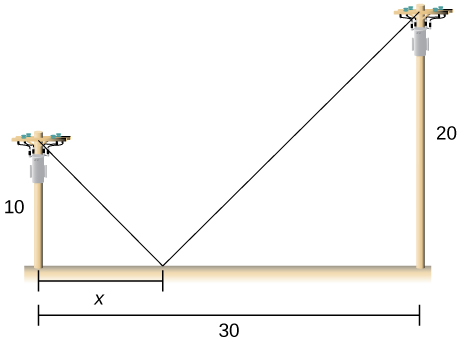
- Answer
-
Under Construction
Exercise \(\PageIndex{7}\)
You are moving into a new apartment and notice there is a corner where the hallway narrows from 8ft to 6ft. What is the length of the longest item that can be carried horizontally around the corner?
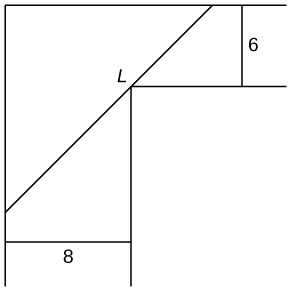
- Answer
-
19.73 ft
Exercise \(\PageIndex{8}\)
1) A patient’s pulse measures 70bpm,80bpm, then 120bpm. To determine an accurate measurement of pulse, the doctor wants to know what value minimizes the expression \((x−70)^2+(x−80)^2+(x−120)^2\)?
2) In the previous problem, assume the patient was nervous during the third measurement, so we only weight that value half as much as the others. What is the value that minimizes \((x−70)^2+(x−80)^2+12(x−120)^2\)?
- Answer
-
84bpm
Exercise \(\PageIndex{9}\)
You can run at a speed of 66 mph and swim at a speed of 33 mph and are located on the shore, 44 miles east of an island that is 11 mile north of the shoreline. How far should you run west to minimize the time needed to reach the island?
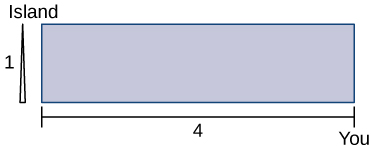
- Answer
-
Under Construction
Exercise \(\PageIndex{10}\)
For the following problems, consider a lifeguard at a circular pool with diameter 40m. He must reach someone who is drowning on the exact opposite side of the pool, at position C. The lifeguard swims with a speed v and runs around the pool at speed w=3v.
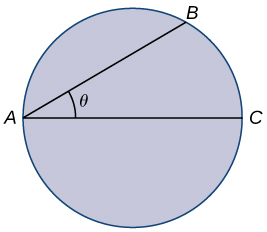
1) Find a function that measures the total amount of time it takes to reach the drowning person as a function of the swim angle, θ.
2) Find at what angle θ the lifeguard should swim to reach the drowning person in the least amount of time.
- Answer
-
Under Construction
Exercise \(\PageIndex{11}\)
For the following exercises, consider a limousine that gets \(m(v)=(120−2v)5mi/gal \)at speed v, the chauffeur costs $15/h, and gas is $3.5/gal.
1) Find the cost per mile at speed v.
2) Find the cheapest driving speed.
- Answer
-
Approximately 34.02mph
Exercise \(\PageIndex{12}\)
For the following exercises, consider a pizzeria that sell pizzas for a revenue of \(R(x)=ax\) and costs \(C(x)=b+cx+dx^2\), where x represents the number of pizzas.
1) Find the profit function for the number of pizzas. How many pizzas gives the largest profit per pizza?
2) Assume that \(R(x)=10x\) and \(C(x)=2x+x^2\). How many pizzas sold maximizes the profit?
- Answer
-
44
3) Assume that \(R(x)=15x\), and \(C(x)=60+3x+12x^2\). How many pizzas sold maximizes the profit?
Exercise \(\PageIndex{13}\)
Consider a wire 4ft long cut into two pieces. One piece forms a circle with radius r and the other forms a square of side x.
Choose x to maximize the sum of their areas.
- Answer
-
Under Construction
Exercise \(\PageIndex{14}\)
For the following exercises, consider two non-negative numbers x and y such that \(x+y=10\). Maximize and minimize the quantities.
1) \(xy\)
- Answer
-
Maximal: \(x=5,y=5\); minimal:\(x=0, y=10x=0, y=10\) and \(y=0, x=10y=0, x=10\)
2) \(x^2 y^2\)
3) \(y−1x\)
- Answer
-
Maximal: \(x=1,y=9\); minimal: none
4) \(x^2-y\)
Exercise \(\PageIndex{15}\)
For the following exercises, draw the given optimization problem and solve.
1) Find the volume of the largest right circular cylinder that fits in a sphere of radius 11.
- Answer
-
Under Construction
2) Find the volume of the largest right cone that fits in a sphere of radius 11.
3) Find the area of the largest rectangle that fits into the triangle with sides x=0,y=0 and \(x^4+y^6=1\)
- Answer
-
Under Construction
4) Find the largest volume of a cylinder that fits into a cone that has base radius R and height h.
5) Find the dimensions of the closed cylinder volume V=16π that has the least amount of surface area.
- Answer
-
r=2,h=4
6) Find the dimensions of a right cone with surface area S=4π that has the largest volume.
Exercise \(\PageIndex{16}\)
For the following exercises, consider the points on the given graphs. Use a calculator to graph the functions.
1) Where is the line \(y=5−2x\) closest to the origin?
- Answer
-
(2,1)
2) Where is the line y=5−2x closest to point (1,1)?
3) Where is the parabola \(y=x^2\) closest to point (2,0)?
- Answer
-
(0.8351,0.6974)
4) Where is the parabola \(y=x^2\) closest to point (0,3)?
Exercise \(\PageIndex{17}\)
For the following exercises, set up, but do not evaluate, each optimization problem.
1) A window is composed of a semicircle placed on top of a rectangle. If you have 20ft of window-framing materials for the outer frame, what is the maximum size of the window you can create? Use r to represent the radius of the semicircle.

- Answer
-
\(A=20r−2r^2−12πr^2\)
2) You have a garden row of 20 watermelon plants that produce an average of 30 watermelons apiece. For any additional watermelon plants planted, the output per watermelon plant drops by one watermelon. How many extra watermelon plants should you plant?
3) You are constructing a box for your cat to sleep in. The plush material for the square bottom of the box costs \($5/ft^2\) and the material for the sides costs \($2/ft^2\). You need a box with volume \(4ft^2\). Find the dimensions of the box that minimize cost. Use x to represent the length of the side of the box.
- Answer
-
\(C(x)=5x^2+32x\)
4) You are building five identical pens adjacent to each other with a total area of \(1000m^2\), as shown in the following figure. What dimensions should you use to minimize the amount of fencing?
5) You are the manager of an apartment complex with 50 units. When you set rent at $800/month, all apartments are rented. As you increase rent by $25/month, one fewer apartment is rented. Maintenance costs run $50/month for each occupied unit. What is the rent that maximizes the total amount of profit?
- Answer
-
\(P(x)=(50−x)(800+25x−50)\)

