2.1: Binary Relations
- Page ID
- 7426
This page is a draft and is under active development.
Definition: Binary Relation
Let \(S\) be a non-empty set. Then any subset \(R\) of \(S \times S\) is said to be a relation over \(S\). In other words, a relation is a rule that is defined between two elements in \(S\). Intuitively, if \(R\) is a relation over \(S\), then the statement \(a R b\) is either true or false for all \(a,b\in S\).
If the statement \(a R b\) is false, we denote this by \( a \not R b\).
Example \(\PageIndex{1}\):
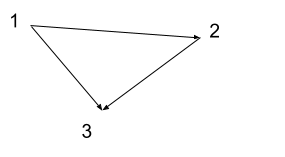
Let \(S=\{1,2,3\}\). Define \(R\) by \(a R b\) if and only if \(a < b\), for \(a, b \in S\).
Then \(1 R 2, 1 R 3, 2 R 3 \) and \( 2 \not R 1\).
We can visualize the above binary relation as a graph, where the vertices are the elements of S, and there is an edge from \(a\) to \(b\) if and only if \(a R b\), for \(a b\in S\).
The following are some examples of relations defined on \(\mathbb{Z}\).
Example \(\PageIndex{2}\):
- Define \(R\) by \(a R b\) if and only if \(a < b\), for \(a, b \in \mathbb{Z}\).
- Define \(R\) by \(a R b\) if and only if \(a >b\), for \(a, b \in \mathbb{Z}\).
- Define \(R\) by \(a R b\) if and only if \(a \leq b\), for \(a, b \in \mathbb{Z}\).
- Define \(R\) by \(a R b\) if and only if \(a \geq b\), for \(a, b \in \mathbb{Z}\).
- Define \(R\) by \(a R b\) if and only if \(a = b\), for \(a, b \in \mathbb{Z}\).
Multiples and divisors
Next, we will introduce the notion of "divides."
Definition: Divisor/Divides
Let \( a\) and \(b\) be integers. We say that \(a\) divides \(b\) is denoted \(a\mid b\), provided we have an integer \(m\) such that \(b=am\). In this case we can also say the following:
- \(b\) is divisible by \(a\)
- \(a\) is a factor of \(b\)
- \(a\) is a divisor of \(b\)
- \(b\) is a multiple of \(a\)
If \(a\) does not divide \(b\), then it is is denoted by \(a \not \mid b\).
Example \(\PageIndex{3}\):
Find all positive integers divisible by \(16.\)
Solution
Multiples of \(16. \)
Example \(\PageIndex{4}\):
Find all positive integers divides \(16.\)
Solution
\(1, 2, 4, 8, 16\)
Example \(\PageIndex{5}\):
\(4 \mid 12\) and \(12 \not\mid 4\)
Next, we will introduce the notion of "divides" for positive integers.
Definition: Divides
Let \( a\) and \(b\) be positive integers. We say that \(a\) divides \(b\) is denoted \(a\mid b\), there exists a positive integer \(m\) such that \(b=am\).
Theorem \(\PageIndex{1}\): Divisibility inequality theorem
If \(a\mid b\), for \(a, b \in \mathbb{Z_+}\) then \(a \leq b\),
- Proof
-
Let \(a, b \in \mathbb{Z_+}\) such that \(a\mid b\), Since (a\mid b\), there is a positive integer \(m\) such that \(b=am\). Since \(m \geq 1\) and \(a\) is a positive integer, \(b=am \geq (a)(1)=a. \)
Note that if \(a\mid b\), for \(a, b \in \mathbb{Z_+}\) then \(a \leq b\), but the converse is not true. For example: \(2 <3\), but \(2 \not\mid 3\).
Example \(\PageIndex{6}\):
According to our definition \(0 \mid 0\).
Definition: Even integer
An integer is even provided that it is divisible by \(2\).
Properties of binary relation:
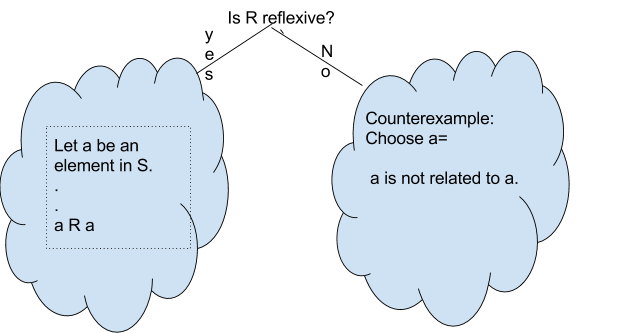
Definition: Reflexive
Let \(S\) be a set and \(R\) be a binary relation on \(S\). Then \(R\) is said to be reflexive if \( a R a, \forall a \in S.\)
Example \(\PageIndex{5}\): Visually

\(\forall a \in S, a R a\) holds.
We will follow the template below to answer the question about reflexive.
Example \(\PageIndex{7}\):
Define \(R\) by \(a R b\) if and only if \(a < b\), for \(a, b \in \mathbb{Z}\). Is \(R\) reflexive?
Counter Example:
Choose \(a=2.\)
Since \( 2 \not< 2\), \(R\) is not reflexive.
Example \(\PageIndex{8}\):
Define \(R\) by \(a R b\) if and only if \(a \mid b\), for \(a, b \in \mathbb{Z}\). Is \(R\) reflexive?
Proof:
Let \( a \in \mathbb{Z}\). Since \(a=(1) (a)\), \(a \mid a\).
Thus \(R\) is reflexive. \( \Box\)
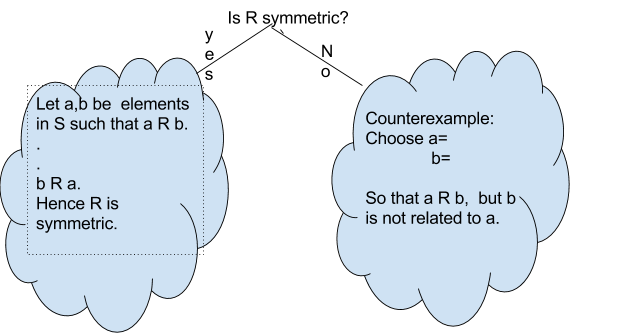
Definition: Symmetric
Let \(S\) be a set and \(R\) be a binary relation on \(S\). Then \(R\) is said to be symmetric if the following statement is true:
\( \forall a,b \in S\), if \( a R b \) then \(b R a\), in other words, \( \forall a,b \in S, a R b \implies b R a.\)
Example \(\PageIndex{8}\): Visually

\(\forall a,b \in S, a R b \implies b R a.\) holds!
We will follow the template below to answer the question about symmetric.
Example \(\PageIndex{9}\):
Define \(R\) by \(a R b\) if and only if \(a < b\), for \(a, b \in \mathbb{Z}\). Is \(R\) symmetric?
Counter Example:
\(1<2\) but \(2 \not < 1\).
Example \(\PageIndex{10}\):
Define \(R\) by \(a R b\) if and only if \(a \mid b\), for \(a, b \in \mathbb{Z}\). Is \(R\) symmetric?
Counter Example:
\(2 \mid 4\) but \(4 \not \mid 2\).
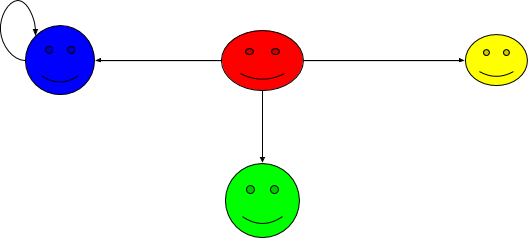
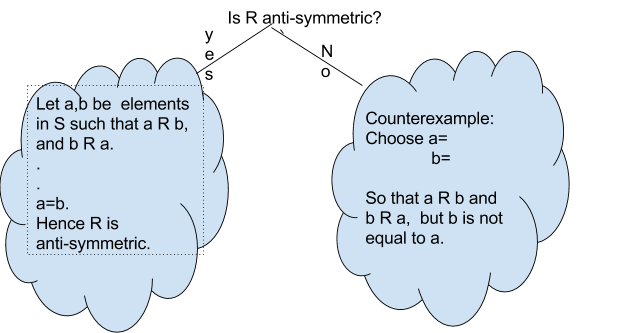
Definition: Antisymmetric
Let \(S\) be a set and \(R\) be a binary relation on \(S\). Then \(R\) is said to be antisymmetric if the following statement is true:
\( \forall a,b \in S\), if \( a R b \) and \(b R a\), then \(a=b\).
In other words, \( \forall a,b \in S\), \( a R b \wedge b R a \implies a=b.\)
Example \(\PageIndex{11}\): VISUALLY
\( \forall a,b \in S\), \( a R b \wedge b R a \implies a=b \) holds!
We will follow the template below to answer the question about anti-symmetric.
Example \(\PageIndex{12}\):
Define \(R\) by \(a R b\) if and only if \(a < b\), for \(a, b \in \mathbb{Z}\). Is \(R\) antisymmetric?
Example \(\PageIndex{13}\):
Define \(R\) by \(a R b\) if and only if \(a \mid b\), for \(a, b \in \mathbb{Z_+}\). Is \(R\) antisymmetric?
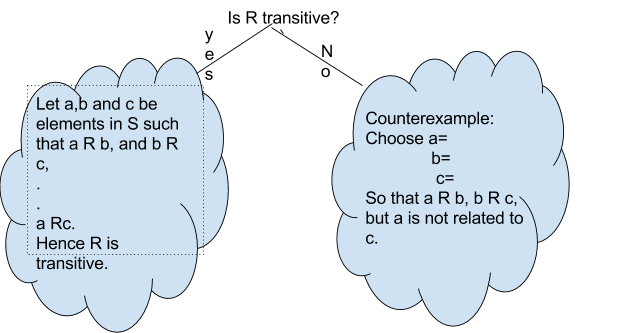
Definition: Transitive
Let \(S\) be a set and \(R\) be a binary relation on \(S\). Then \(R\) is said to be transitive if the following statement is true
\( \forall a,b,c \in S,\) if \( a R b \) and \(b R c\), then \(a R c\).
In other words, \( \forall a,b,c \in S\), \( a R b \wedge b R c \implies a R c\).
Example \(\PageIndex{14}\): VISUALLY
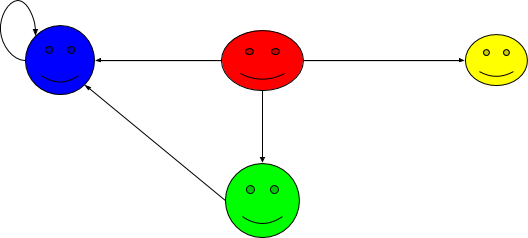
\( \forall a,b,c \in S\), \( a R b \wedge b R c \implies a R c\) holds!
We will follow the template below to answer the question about transitive.
Example \(\PageIndex{15}\):
Define \(R\) by \(a R b\) if and only if \(a < b\), for \(a, b \in \mathbb{Z}\). Is \(R\) transitive?
Example \(\PageIndex{16}\):
Define \(R\) by \(a R b\) if and only if \(a \mid b\), for \(a, b \in \mathbb{Z_+}\). Is \(R\) transitive?
Summary:
In this section, we learned about binary relations and the following properties:
Reflexive
Symmetric
Antisymmetric
Transitive


