1.1: Volumes of solids of revolution -cross-sections
This page is a draft and is under active development.
( \newcommand{\kernel}{\mathrm{null}\,}\)
In this section, we use definite integrals to find volumes of three-dimensional solids. We consider three approaches—slicing, disks, and washers—for finding these volumes, depending on the characteristics of the solid.
Volume and the Slicing Method
Just as area is the numerical measure of a two-dimensional region, volume is the numerical measure of a three-dimensional solid. Most of us have computed volumes of solids by using basic geometric formulas. The volume of a rectangular solid, for example, can be computed by multiplying length, width, and height: V=lwh. The formulas for the volumes of:
- a sphere
Vsphere=43πr3,
- a cone
Vcone=13πr2h
- and a pyramid
Vpyramid=13Ah
have also been introduced. Although some of these formulas were derived using geometry alone, all these formulas can be obtained by using integration.
We can also calculate the volume of a cylinder. Although most of us think of a cylinder as having a circular base, such as a soup can or a metal rod, in mathematics the word cylinder has a more general meaning. To discuss cylinders in this more general context, we first need to define some vocabulary.
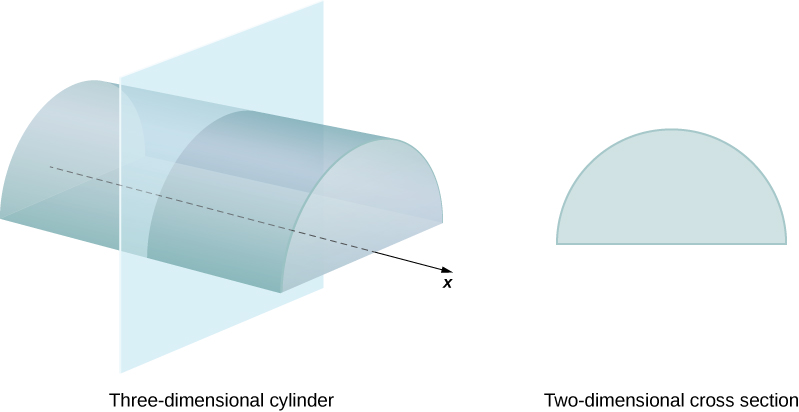
We define the cross-section of a solid to be the intersection of a plane with the solid. A cylinder is defined as any solid that can be generated by translating a plane region along a line perpendicular to the region, called the axis of the cylinder. Thus, all cross-sections perpendicular to the axis of a cylinder are identical. The solid shown in Figure is an example of a cylinder with a noncircular base. To calculate the volume of a cylinder, then, we simply multiply the area of the cross-section by the height of the cylinder: V=A⋅h. In the case of a right circular cylinder (soup can), this becomes V=πr2h.
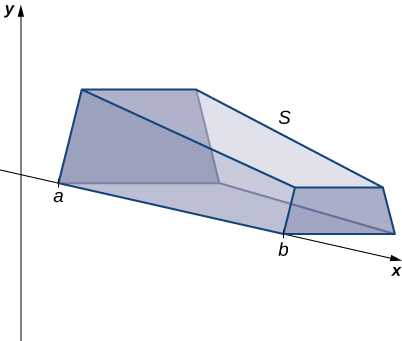
If a solid does not have a constant cross-section (and it is not one of the other basic solids), we may not have a formula for its volume. In this case, we can use a definite integral to calculate the volume of the solid. We do this by slicing the solid into pieces, estimating the volume of each slice, and then adding those estimated volumes together. The slices should all be parallel to one another, and when we put all the slices together, we should get the whole solid. Consider, for example, the solid S shown in Figure, extending along the x-axis.
We want to divide S into slices perpendicular to the x-axis. As we see later in the chapter, there may be times when we want to slice the solid in some other direction—say, with slices perpendicular to the y-axis. The decision of which way to slice the solid is very important. If we make the wrong choice, the computations can get quite messy. Later in the chapter, we examine some of these situations in detail and look at how to decide which way to slice the solid. For the purposes of this section, however, we use slices perpendicular to the x-axis.
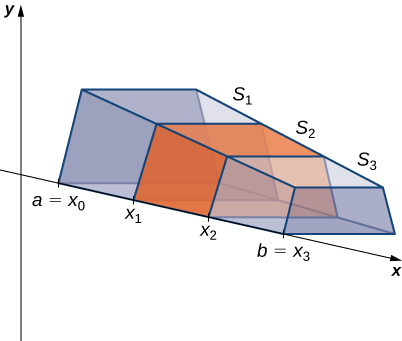
Because the cross-sectional area is not constant, we let A(x) represent the area of the cross-section at point x. Now let P=x0,x1…,Xn be a regular partition of [a,b], and for i=1,2,…n, let Si represent the slice of S stretching from xi−1 to xi. The following figure shows the sliced solid with n=3.
Finally, for i=1,2,…n, let x∗i be an arbitrary point in [xi−1,xi]. Then the volume of slice Si can be estimated by V(Si)≈A(x∗i)Δx. Adding these approximations together, we see the volume of the entire solid S can be approximated by
V(S)≈n∑i=1A(x∗i)Δx.
By now, we can recognize this as a Riemann sum, and our next step is to take the limit as n→∞. Then we have
V(S)=limn→∞n∑i=1A(x∗i)Δx=∫abA(x)dx.
The technique we have just described is called the slicing method. To apply it, we use the following strategy.
Problem-Solving Strategy: Finding Volumes by the Slicing Method
- Examine the solid and determine the shape of a cross-section of the solid. It is often helpful to draw a picture if one is not provided.
- Determine a formula for the area of the cross-section.
- Integrate the area formula over the appropriate interval to get the volume.
Recall that in this section, we assume the slices are perpendicular to the x-axis. Therefore, the area formula is in terms of x and the limits of integration lie on the x-axis. However, the problem-solving strategy shown here is valid regardless of how we choose to slice the solid.
Example 1.1.1: Deriving the Formula for the Volume of a Pyramid
We know from geometry that the formula for the volume of a pyramid is V=13Ah. If the pyramid has a square base, this becomes V=13a2h, where a denotes the length of one side of the base. We are going to use the slicing method to derive this formula.
Solution
We want to apply the slicing method to a pyramid with a square base. To set up the integral, consider the pyramid shown in Figure, oriented along the x-axis.
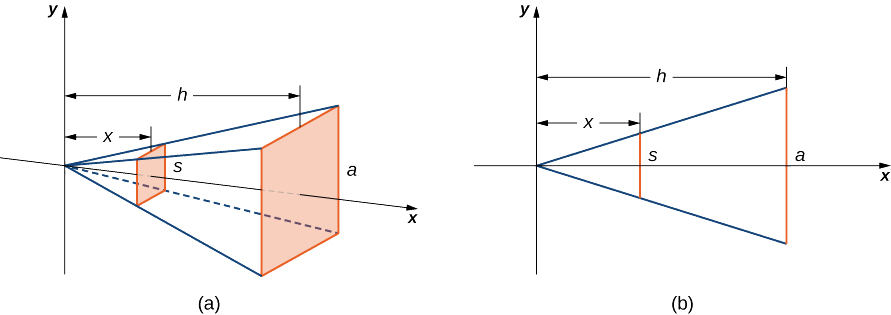
We first want to determine the shape of a cross-section of the pyramid. We are know the base is a square, so the cross-sections are squares as well (step 1). Now we want to determine a formula for the area of one of these cross-sectional squares. Looking at Figure(b), and using a proportion, since these are similar triangles, we have
sa=xh
or
s=axh.
Therefore, the area of one of the cross-sectional squares is
A(x)=s2=(axh)2(step2).
Then we find the volume of the pyramid by integrating from 0 to h (step 3):
V=∫h0A(x)dx=∫h0(axh)2dx=a2h2∫h0x2dx=[a2h2(13x3)]|h0=13a2h.
This is the formula we were looking for.
Exercise 1.1.1
Use the slicing method to derive the formula V=13πr2h
- Hint
-
Use similar triangles, as in the Example. Consider what the shape of a slice is.
- Answer
-
First, we want to determine the shape of a cross section of this circular cone. As the name states, we expect the cross section to be a circle. Knowing the formula for the area of a circle, ACircle=πr2, we can now find the value of r using similar triangles. This process was used above to solve for a pyramid with a square base.
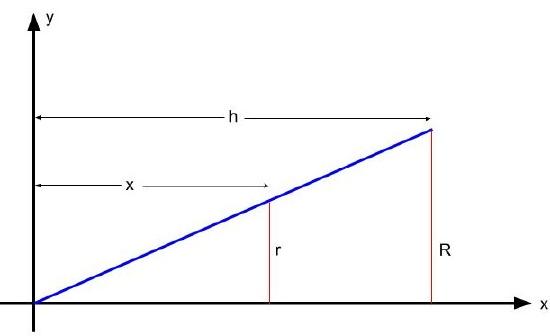
Notice the ratio of similar triangles is: rR=xh.
or r=Rxh.
Substituting into the formula for area we get: A(x)=πr2=π(Rxh)2.
Now, if we consider this circle as a very, very thin disc, with thickness dx and radius r, where r=Rxh.
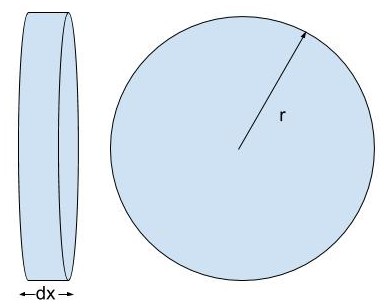
We can write an equation for the volume of this very, very thin disc. dV=π(Rxh)2dx.
Taking the complete distance of the cone from base to point as h we can establish bounds for integration and solve for the area of the cone. V=∫h0A(x)dx=πR2h2∫h0x2dx=[πR2h2(13x3)]h0=13πR2hunits3
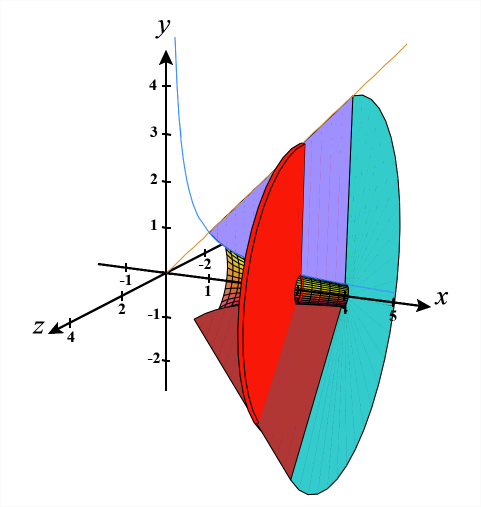
Find the volume of the solid whose base is the region bounded by the curves y=3x2 and y=1−x2, and whose cross-sections through the solid perpendicular to the x-axis are squares.
Solution
You can view the diagram here: https://www.geogebra.org/3d/k67duzz4
Find the intersecting points:
1−x2=3x2⟹4x2=1⟹x=±12.
Now, length of the slice (square) at x is 1−x2−3x2=1−4x2.
Since the slice is a square, A(x)=(1−4x2)2=1−8x2+16x4.
Hence the volume of the solid is V=∫12−121−8x2+16x4dx=(x−8x33+16x55)|12−12=715units3.
Solids of Revolution
If a region in a plane is revolved around a line in that plane, the resulting solid is called a solid of revolution, as shown in the following figure.
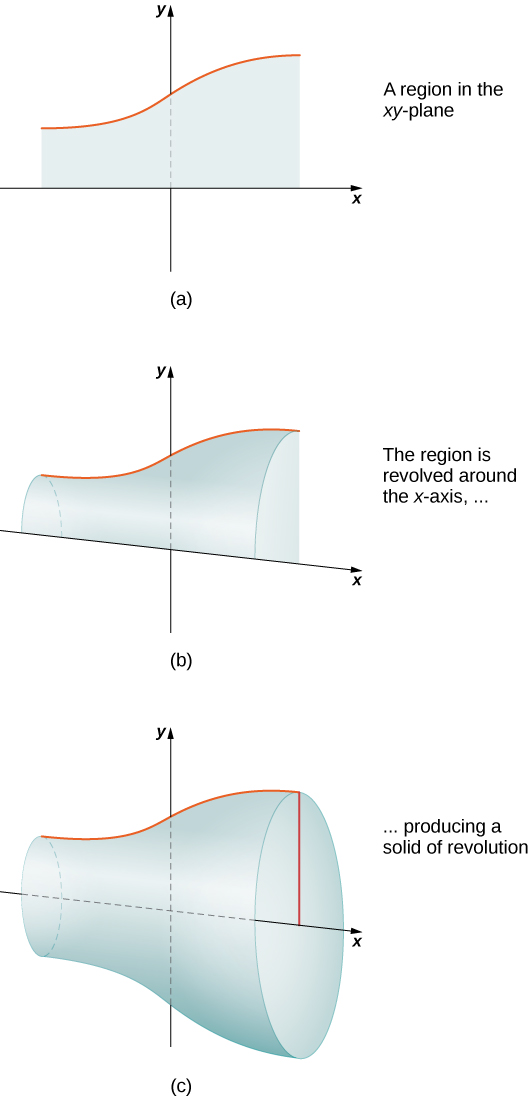
Solids of revolution are common in mechanical applications, such as machine parts produced by a lathe. We spend the rest of this section looking at solids of this type. The next example uses the slicing method to calculate the volume of a solid of revolution.
Example 1.1.3: Using the Slicing Method to find the Volume of a Solid of Revolution
Use the slicing method to find the volume of the solid of revolution bounded by the graphs of f(x)=x2−4x+5,x=1,and x=4, and rotated about the x-axis.
Solution
Using the problem-solving strategy, we first sketch the graph of the quadratic function over the interval [1,4] as shown in the following figure.
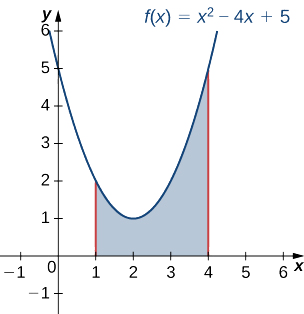
Next, revolve the region around the x-axis, as shown in the following figure.
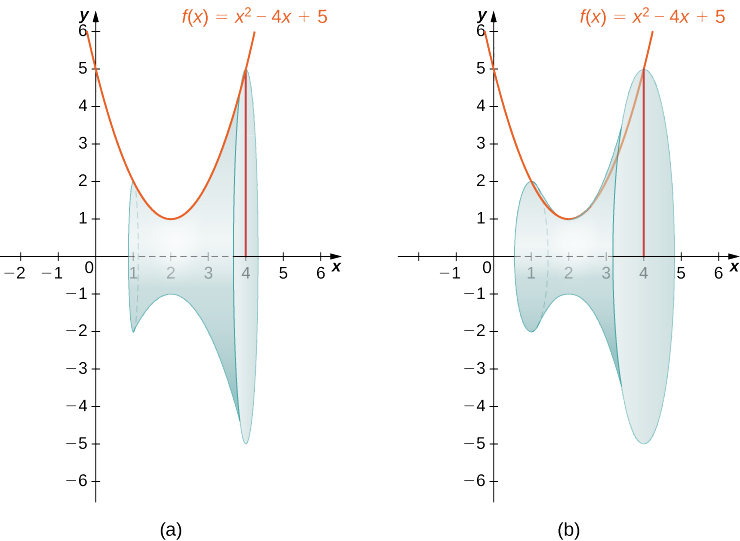
Visualize here: https://www.geogebra.org/3d/dvyuyzer
Since the solid was formed by revolving the region around the x-axis, the cross-sections are circles (step 1). The area of the cross-section, then, is the area of a circle, and the radius of the circle is given by f(x). Use the formula for the area of the circle:
A(x)=πr2=π[f(x)]2=π(x2−4x+5)2(step2).
The volume, then, is (step 3)
V=∫ahA(x)dx=∫41π(x2−4x+5)2dx=π∫41(x4−8x3+26x2−40x+25)dx=π(x55−2x4+26x33−20x2+25x)|41=785π
The volume is \(78π/5 \text{units}^3.\)
Exercise 1.1.2
Use the method of slicing to find the volume of the solid of revolution formed by revolving the region between the graph of the function f(x)=1/x and the x-axis over the interval [1,2] around the x-axis. See the following figure.
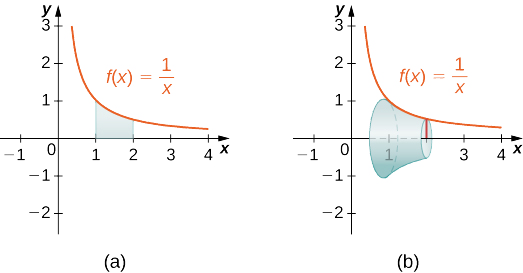
- Hint
-
Use the problem-solving strategy presented earlier. Always consider the dimensions for the disk. What is the radius?
- Answer
-
Since the solid was formed by revolving about the x-axis, the cross sections will be circles. The ares of the cross section is that of a circle. with the radius being f(x). The area can be written as follows:A(x)=πr2=π(1x)2=π(1x2).
Expressing this as a volume for a thin disc we get: dV=π(1x2)dx
Now taking the definite integral within the interval [1,2] we can solve for the volume of the solid.V=π∫21(1x2)dx=π[−1x]21=π[−12+1]=π2
The Disk Method
When we use the slicing method with solids of revolution, it is often called the disk method because, for solids of revolution, the slices used to over approximate the volume of the solid are disks. To see this, consider the solid of revolution generated by revolving the region between the graph of the function f(x)=(x−1)2+1 and the x-axis over the interval [−1,3] around the x-axis. The graph of the function and a representative disk are shown in Figure(a) and (b). The region of revolution and the resulting solid are shown in Figure(c) and (d).
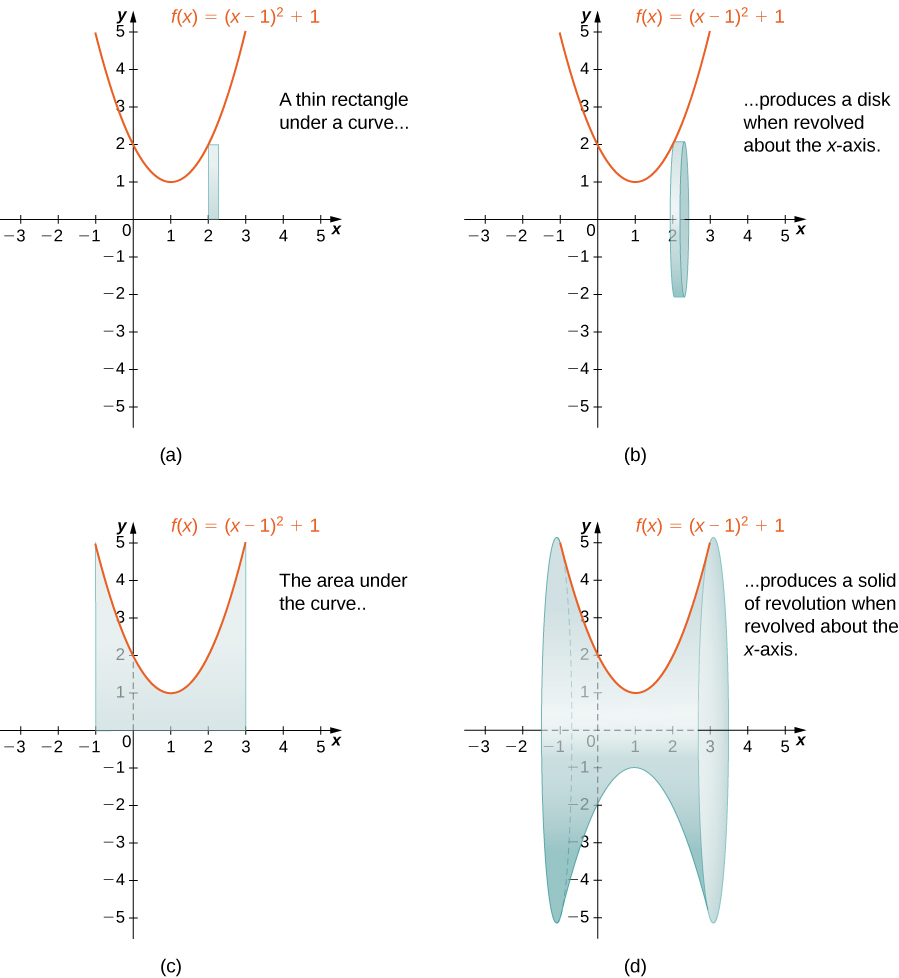
Figure 1.1.8: (e) A dynamic version of this solid of revolution generated using CalcPlot3D.
We already used the formal Riemann sum development of the volume formula when we developed the slicing method. We know that ∫baA(x)dx.
The only difference with the disk method is that we know the formula for the cross-sectional area ahead of time; it is the area of a circle. This gives the following rule.
The Disk Method
Let f(x) be continuous and nonnegative. Define R as the region bounded above by the graph of f(x), below by the x-axis, on the left by the line x=a, and on the right by the line x=b. Then, the volume of the solid of revolution formed by revolving R around the x-axis is given by
V=∫baπ[f(x)]2dx.
The volume of the solid we have been studying (Figure 1.1.8) is given by
V=∫baπ[f(x)]2dx=∫3−1π[(x−1)2+1]2dx=π∫3−1[(x−1)4+2(x−1)2+1]2dx=π[15(x−1)5+23(x−1)3+x]|3−1=π[(325+163+3)−(−325−163−1)]=412π15units3.
Let’s look at some examples.
Example 1.1.4: Using the Disk Method to Find the Volume of a Solid of Revolution 1
Use the disk method to find the volume of the solid of revolution generated by rotating the region between the graph of f(x)=√x and the x-axis over the interval [1,4] around the x-axis.
Solution
The graphs of the function and the solid of revolution are shown in the following figure.
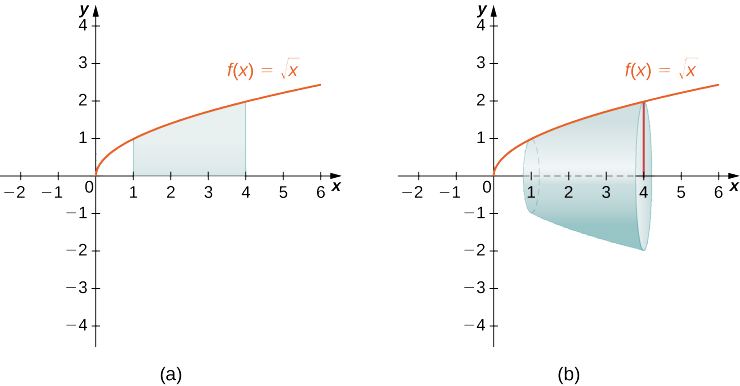
Visualize here: https://www.geogebra.org/3d/vc3gepfq
We have
V=∫baπ[f(x)]2dx
=∫41π[√x]2dx=π∫41xdx
=π2x2|41=15π2
The volume is (15π)/2 units3.
Exercise 1.1.3
Use the disk method to find the volume of the solid of revolution generated by rotating the region between the graph of f(x)=√4−x and the x-axis over the interval [0,4] around the x-axis.
- Hint
-
Use the procedure from Example. Always draw a picture for yourself. What are the dimensions of the disk? What is its Thickness? Radius?
- Answer
-
The first step in the solution of this problem involves identifying the radius of our disc. In this problem the radius is f(x)=√4−x. Using this radius we can use the formula for the area of a circle, radius f(x). This resulting area is: A(x)=π(√4−x)2
And from this area we can write the formula for the volume of a thin disk with thickness dx:dV=π(√4−x)2dx=π(4−x)dx
Taking the definite integral in the interval, [0,4] we get:V=π∫40(4−x)dx=π[4x−12x2]40=8πunits3
So far, our examples have all concerned regions revolved around the x-axis, but we can generate a solid of revolution by revolving a plane region around any horizontal or vertical line. In the next example, we look at a solid of revolution that has been generated by revolving a region around the y-axis. The mechanics of the disk method are nearly the same as when the x-axis is the axis of revolution, but we express the function in terms of y and we integrate with respect to y as well. This is summarized in the following rule.
Rule: The Disk Method for Solids of Revolution around the y-axis
Let g(y) be continuous and nonnegative. Define Q as the region bounded on the right by the graph of g(y), on the left by the y-axis, below by the line y=c, and above by the line y=d. Then, the volume of the solid of revolution formed by revolving Q around the y-axis is given by
V=∫dcπ[g(y)]2dy.
The next example shows how this rule works in practice.
Example 1.1.5: Using the Disk Method to Find the Volume of a Solid of Revolution 2
Let R be the region bounded by the graph of g(y)=√4−y and the y-axis over the y-axis interval [0,4]. Use the disk method to find the volume of the solid of revolution generated by rotating R around the y-axis.
Solution
The figure shows the function and a representative disk that can be used to estimate the volume. Notice that since we are revolving the function around the y-axis, the disks are horizontal, rather than vertical.
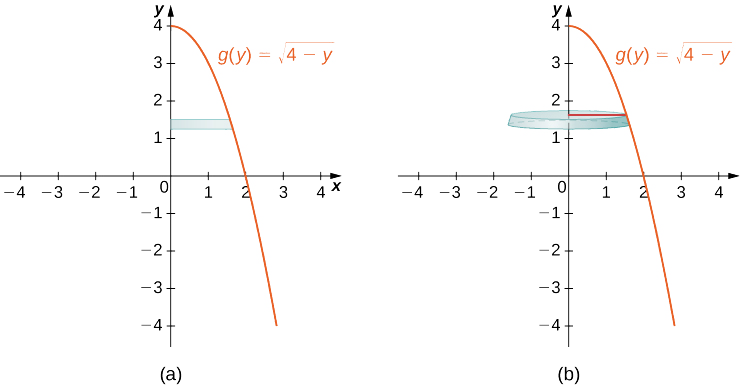
The region to be revolved and the full solid of revolution are depicted in the following figure.
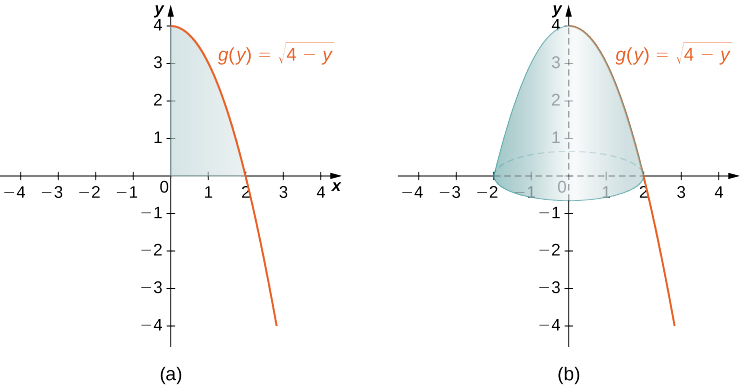
To find the volume, we integrate with respect to y We obtain
V=∫dcπ[g(y)]2dy=∫40π[√4−y]2dy=π∫40(4−y)dy=π[4y−y22]|40=8π.
The volume is 8πunits3.
Exercise 1.1.4
Use the disk method to find the volume of the solid of revolution generated by rotating the region between the graph of g(y)=y and the y-axis over the interval [1,4] around the y-axis.
- Hint
-
Use the procedure from Example. What axis is the solid revolving about? Draw the disk a slice makes. What is its radius?
- Answer
-
Knowing that the solid is rotating around the y-axis we can use the same method as the previous examples. However, in this problem we use g(y) as our radius. This gives us an equation for area:A(y)=πy2
From the area we can establish a volume of a disk with thickness dy (This is dy because the rotation occurs about the y-axis and the thickness of the disk will be parallel to the rotation axis) The volume equation is:dV=πy2dy
Taking the definite integral over the interval [1,4]:V=π∫41y2dy=π[13y3]41=21π
The Washer Method
Some solids of revolution have cavities in the middle; they are not solid all the way to the axis of revolution. Sometimes, this is just a result of the way the region of revolution is shaped with respect to the axis of revolution. In other cases, cavities arise when the region of revolution is defined as the region between the graphs of two functions. A third way this can happen is when an axis of revolution other than the x-axis or y-axis is selected.
When the solid of revolution has a cavity in the middle, the slices used to approximate the volume are not disks, but washers (disks with holes in the center). For example, consider the region bounded above by the graph of the function f(x)=√x and below by the graph of the function g(x)=1 over the interval [1,4]. When this region is revolved around the x-axis, the result is a solid with a cavity in the middle, and the slices are washers. The graph of the function and a representative washer are shown in Figure(a) and (b). The region of revolution and the resulting solid are shown in Figure(c) and (d).
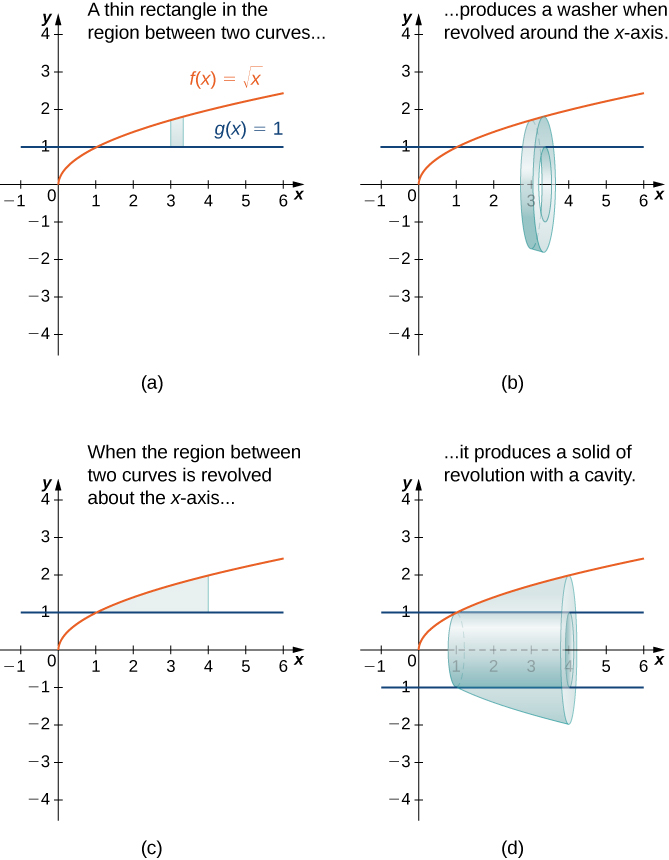
Figure 1.1.12: (e) A dynamic version of this solid of revolution generated using CalcPlot3D.
The cross-sectional area, then, is the area of the outer circle less the area of the inner circle. In this case,
A(x)=π(√x)2−π(1)2=π(x−1).
Then the volume of the solid is
V=∫baA(x)dx=∫41π(x−1)dx=π[x22−x]|41=92πunits3.
Generalizing this process gives the washer method.
Rule: The Washer Method
Suppose f(x) and g(x) are continuous, nonnegative functions such that f(x)≥g(x) over [a,b]. Let R denote the region bounded above by the graph of f(x), below by the graph of g(x), on the left by the line x=a, and on the right by the line x=b. Then, the volume of the solid of revolution formed by revolving R around the x-axis is given by
V=∫baπ[(f(x))2−(g(x))2]dx.
Example 1.1.6: Using the Washer Method
Find the volume of a solid of revolution formed by revolving the region bounded above by the graph of f(x)=x and below by the graph of g(x)=1/x over the interval [1,4] around the x-axis.
Solution
The graphs of the functions and the solid of revolution are shown in the following figure.
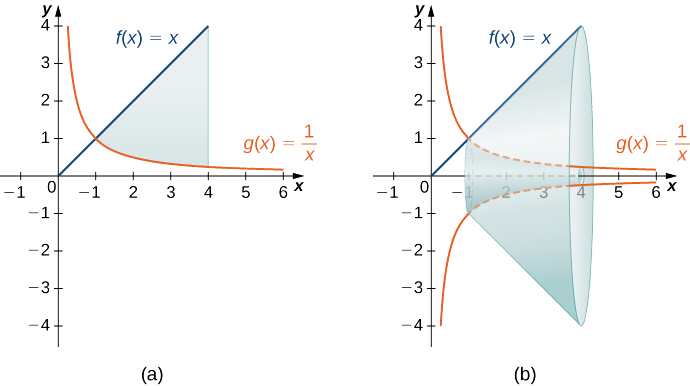
We have
V=∫baπ[(f(x))2−(g(x))2]dx=π∫41[x2−(1x)2]dx=π[x33+1x]|41=81π4units3.
Figure 1.1.13: (c) A dynamic version of this solid of revolution generated using CalcPlot3D.
Exercise 1.1.5
Find the volume of a solid of revolution formed by revolving the region bounded by the graphs of f(x)=√x and g(x)=1/x over the interval [1,3] around the x-axis.
- Hint
-
Graph the functions to determine which graph forms the upper bound and which graph forms the lower bound, then use the procedure from Example.
- Answer
-
The first step in this solution is to graph the functions. This way we can see the section of the graph we need to work with.
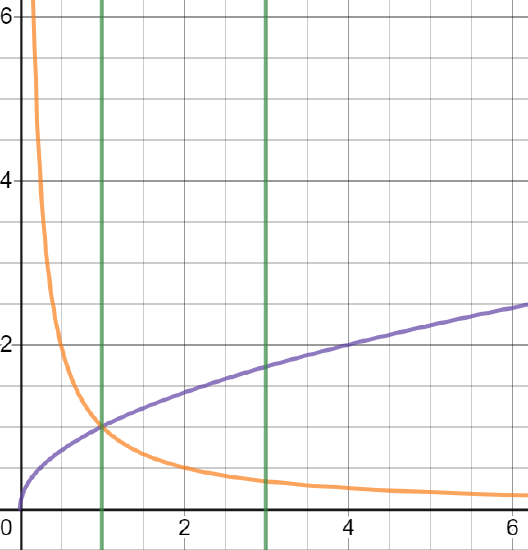
In this graph the purple line is f(x)=√x and the orange is g(x)=1x
Now to setup the washer. As we are revolving around the x-axis, f(x)=√x is the outside of the washer and g(x)=1x is the inside. Following this we subtract the inner portion of the washer from the out portion. This gives us an area of: A(x)=π(√x)2−π(1x)2=π(x−1x2)
Integrating this over our interval [1,3] we get: V=π∫31(x−1x2)dx=π[12x2+1x]31=10π3units3
As with the disk method, we can also apply the washer method to solids of revolution that result from revolving a region around the y-axis. In this case, the following rule applies.
Rule: The Washer Method for Solids of Revolution around the y-axis
Suppose u(y) and v(y) are continuous, nonnegative functions such that v(y)≤u(y) for y∈[c,d]. Let Q denote the region bounded on the right by the graph of u(y), on the left by the graph of v(y), below by the line y=c, and above by the line y=d. Then, the volume of the solid of revolution formed by revolving Q around the y-axis is given by
V=∫dcπ[(u(y))2−(v(y))2]dy.
Other axes of Revolution
Rather than looking at an example of the washer method with the y-axis as the axis of revolution, we now consider an example in which the axis of revolution is a line other than one of the two coordinate axes. The same general method applies, but you may have to visualize just how to describe the cross-sectional area of the volume.
Example 1.1.7:
Find the volume of a solid of revolution formed by revolving the region bounded above by f(x)=4−x and below by the x-axis over the interval [0,4] around the line y=−2.
Solution
The graph of the region and the solid of revolution are shown in the following figure.
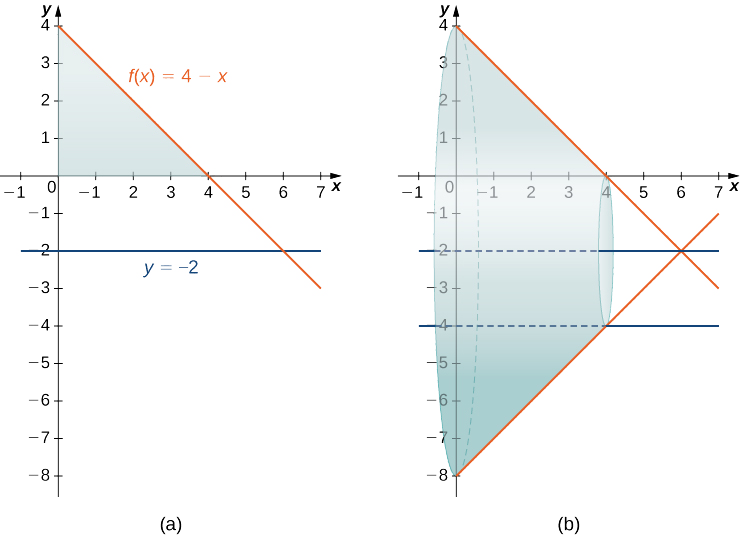
We can’t apply the volume formula to this problem directly because the axis of revolution is not one of the coordinate axes. However, we still know that the area of the cross-section is the area of the outer circle less the area of the inner circle. Looking at the graph of the function, we see the radius of the outer circle is given by f(x)+2, which simplifies to
f(x)+2=(4−x)+2=6−x.
The radius of the inner circle is g(x)=2. Therefore, we have
V=∫40π[(6−x)2−(2)2]dx=π∫40(x2−12x+32)dx=π[x33−6x2+32x]|40=160π3units3.
Figure 1.1.14: (c) A dynamic version of this solid of revolution generated using CalcPlot3D.
Exercise 1.1.6
Find the volume of a solid of revolution formed by revolving the region bounded above by the graph of f(x)=x+2 and below by the x-axis over the interval [0,3] around the line y=−1.
- Hint
-
Use the procedure from Example. What is outer portion of the washer? What is the inner? Did you graph the functions over the interval?
- Answer
-
As before the first step in the solution is to graph the functions and identify the out and inner potions of our washer.
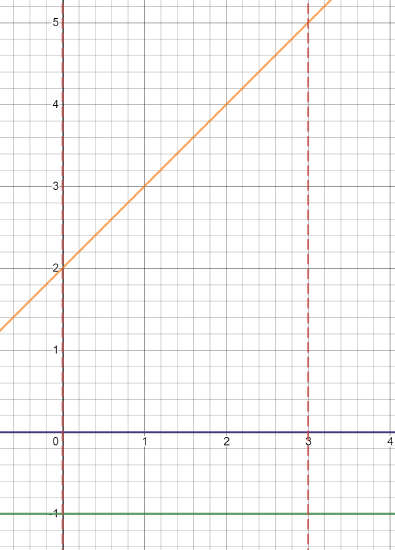
In the graph the orange line represents f(x)=x+2, the purple line represents the x-axis, the green represents the line we are rotating about, and the red are the bounds of integration.
The first step in this solution is to find the area of our washer. Since our line of rotation has moved "away" from our function (in this case y=−1 is further from f(x)=x+2 than y=0) so we will add 1 to each side of both our disks. Our new equations will be: f(x)+1=(x+2)+1=x+3 and y=g(x)=0+1=1
Substituting these values into our washer area formula we arrive at:A(x)=π[(x+3)2−12]=π(x2+6x+8)
Now integrating over the interval [0,3] we get: V=π∫30(x2+6x+8)dx=π[13x3+3x2+8x]30=60πunits3
Key Concepts
- Definite integrals can be used to find the volumes of solids. Using the slicing method, we can find a volume by integrating the cross-sectional area.
- For solids of revolution, the volume slices are often disks and the cross-sections are circles. The method of disks involves applying the method of slicing in the particular case in which the cross-sections are circles and using the formula for the area of a circle.
- If a solid of revolution has a cavity in the center, the volume slices are washers. With the method of washers, the area of the inner circle is subtracted from the area of the outer circle before integrating.
Key Equations
- Disk Method along the x-axis
V=∫baπ[f(x)]2dx
- Disk Method along the y-axis
V=∫dcπ[g(y)]2dy
- Washer Method
V=∫baπ[(f(x))2−(g(x))2]dx
Glossary
- cross-section
- the intersection of a plane and a solid object
- disk method
- a special case of the slicing method used with solids of revolution when the slices are disks
- slicing method
- a method of calculating the volume of a solid that involves cutting the solid into pieces, estimating the volume of each piece, then adding these estimates to arrive at an estimate of the total volume; as the number of slices goes to infinity, this estimate becomes an integral that gives the exact value of the volume.
- solid of revolution
- a solid generated by revolving a region in a plane around a line in that plane.
- washer method
- a special case of the slicing method used with solids of revolution when the slices are washers
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.